Современные проблемы физики / PhysicalReviewpdf / Andreev-1

© А̉‚ А.Ç., 2000

“SUPERRELATIVISTIC” PULSE PROPAGATION

IN RESONANT AMPLIFYING MEDIA

A. V. ANDREEV

By comparing the equations for a mathematical pendulum and harmonic oscillator and taking as an example the nonlinear regime of pulse propagation in a resonant media, we discuss the main differences between linear and nonlinear systems. We show that the dynamics of the nonlinear optical processes has some analogies with the non-optical phenomena.

з‡ Т ‡‚МВМЛЛ П‡ЪВП‡ЪЛ˜ВТНУ„У П‡flЪМЛН‡ Л „‡ ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡ Л М‡ Ф ЛПВ-В МВОЛМВИМ˚ı УФЪЛ˜ВТНЛı Б‡‰‡˜, Т‚flБ‡М- М˚ı Т ‡ТФ УТЪ ‡МВМЛВП ЛПФЫО¸ТУ‚ ‚ ВБУ- М‡МТМ˚ı Т В‰‡ı, У·ТЫК‰‡˛ЪТfl УЪОЛ˜Лfl ОЛМВИМ˚ı Л МВОЛМВИМ˚ı ТЛТЪВП. иУН‡Б‡МУ, ˜ЪУ ‰ЛМ‡ПЛН‡ МВОЛМВИМ˚ı УФЪЛ˜ВТНЛı Ф У- ˆВТТУ‚ ЛПВВЪ ‡М‡ОУ„ЛЛ Т МВУФЪЛ˜ВТНЛПЛ ‚Б‡ЛПУ‰ВИТЪ‚ЛflПЛ.

www.issep.rssi.ru

ЗЗЦСЦзаЦ

З ФУТОВ‰МЛВ 25–30 ОВЪ ‚ ‡БОЛ˜М˚ı У·О‡ТЪflı ЩЛБЛНЛ Л П‡ЪВП‡ЪЛНЛ М‡ ФВ В‰МЛИ ФО‡М ‚˚ıУ‰flЪ МВОЛМВИМ˚В Б‡- ‰‡˜Л. нВУ ЛЛ, УТМУ‚‡ММ˚В М‡ ЛТФУО¸БУ‚‡МЛЛ ОЛМВИМ˚ı НО‡ТТЛ˜ВТНЛı ЛОЛ Н‚‡МЪУ‚˚ı Ы ‡‚МВМЛИ, Т˚„ ‡ОЛ УФ-В‰ВОfl˛˘Ы˛ УО¸ ‚ ТЪ‡МУ‚ОВМЛЛ ПМУ„Лı У·О‡ТЪВИ М‡Ы- НЛ Л ОВК‡Ъ ‚ УТМУ‚В ТУ‚ ВПВММ˚ı Ф В‰ТЪ‡‚ОВМЛИ У· УН-ЫК‡˛˘ВП М‡Т ПЛ В. й‰М‡НУ flТМУ, ˜ЪУ Н‡ ЪЛМ‡ ПЛ ‡, ФУТЪ УВММ‡fl М‡ ОЛМВИМ˚ı Ы ‡‚МВМЛflı, ЛПВВЪ У„ ‡МЛ- ˜ВММЫ˛ У·О‡ТЪ¸ Ф ЛПВМВМЛfl, ФУТНУО¸НЫ ‚ТВ ОЛМВИМ˚В Ф УˆВТТ˚ ‡МУ ЛОЛ ФУБ‰МУ ТЪ‡МУ‚flЪТfl МВОЛМВИМ˚ПЛ. аПВММУ МВОЛМВИМУТЪ¸, ФУ-‚Л‰ЛПУПЫ, Л У·ЫТОУ‚ОЛ‚‡ВЪ ‚УБПУКМУТЪ¸ ТЫ˘ВТЪ‚У‚‡МЛfl ТЪ‡·ЛО¸М˚ı ТЪ ЫНЪЫ . З ˝ЪУП М‡Т Ы·ВК‰‡˛Ъ Н‡Н ФУ‚ТВ‰МВ‚М˚И УФ˚Ъ, Ъ‡Н Л У·- ˘ВЩЛОУТУЩТНЛВ ‡ТТЫК‰ВМЛfl. з‡Ф ЛПВ , ОЛМВИМ˚ИУТЪ Ф Л ‡˘ВМЛfl ‰ОЛМ˚ Т УТЪУП Ф ЛОУКВММУИ ТЛО˚ (Б‡НУМ ЙЫН‡) У·˚˜МУ Б‡Н‡М˜Л‚‡ВЪТfl ‡Б ˚‚УП, НУЪУ У- ПЫ Ф В‰¯ВТЪ‚ЫВЪ МВОЛМВИМ˚И ˝Ъ‡Ф. ЗУБПУКВМ Л ‚ЪУ УИ ТˆВМ‡ ЛИ ˝ЪУ„У Ф УˆВТТ‡. ЦТОЛ ЪВОУ УН‡Б‡ОУТ¸ У˜ВМ¸ Ф У˜М˚П Л П˚ МВ ТПУ„ОЛ В„У ‡БУ ‚‡Ъ¸, ЪУ ˝ЪУ УБМ‡˜‡ВЪ, ˜ЪУ ПУ˘МУТЪ¸ ЛТЪУ˜МЛН‡ Ф ЛОУКВММУИ ТЛО˚ ‚˚¯О‡ М‡ М‡Т˚˘ВМЛВ. г˛·УИ ЛТЪУ˜МЛН ЛПВВЪ НУМВ˜МЫ˛ ПУ˘- МУТЪ¸, Л П˚ МВ ПУКВП Ы‚ВОЛ˜Л‚‡Ъ¸ Ф ЛОУКВММЫ˛ ТЛОЫ ‰У ·ВТНУМВ˜МУТЪЛ. з‡ОЛ˜ЛВ М‡Т˚˘ВМЛfl Ъ‡НКВ fl‚ОflВЪТfl Ф Уfl‚ОВМЛВП МВОЛМВИМУТЪЛ ı‡ ‡НЪВ ЛТЪЛН ЛТЪУ˜МЛН‡.

ЙАкейзауЦлдав йлсаггьнйк а еАнЦеАнауЦлдав еАьнзад

д ‡ВЫ„УО¸МУИ ПУ‰ВО¸˛ ПМУ„Лı ОЛМВИМ˚ı ЪВУ ЛИ fl‚ОflВЪТfl ПУ‰ВО¸ „‡ ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡. йМ‡ ОВКЛЪ ‚ УТМУ‚В Н‚‡МЪУ‚˚ı ЪВУ ЛИ ФУОfl, ПЛН У˜‡ТЪЛˆ Л П‡Н У- ТНУФЛ˜ВТНЛı Т В‰. и ЛПВ УП „‡ ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡ fl‚ОflВЪТfl П‡ЪВП‡ЪЛ˜ВТНЛИ П‡flЪМЛН Ф Л МВ У˜ВМ¸ ·УО¸¯Лı ‡ПФОЛЪЫ‰‡ı НУОВ·‡МЛfl. иЫТЪ¸ θ – Ы„УО УЪНОУМВМЛfl П‡flЪМЛН‡ УЪ ФУОУКВМЛfl ‡‚МУ‚ВТЛfl, ЪУ„‰‡ Ы ‡‚- МВМЛВ ‰‚ЛКВМЛfl П‡ЪВП‡ЪЛ˜ВТНУ„У П‡flЪМЛН‡ ЛПВВЪ ıУ-У¯У ЛБ‚ВТЪМ˚И ‚Л‰

„‰Â ω20 = g ⁄ l – ТУ·ТЪ‚ВММ‡fl ˜‡ТЪУЪ‡ НУОВ·‡МЛИ П‡flЪМЛН‡. и Л θ ! 1 Ы ‡‚МВМЛВ (1) Ф ЛМЛП‡ВЪ ‚Л‰ Ы ‡‚МВМЛfl „‡ ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡

З ˜ВП ТУТЪУflЪ УТМУ‚М˚В УЪОЛ˜Лfl МВОЛМВИМУ„У Ы ‡‚МВМЛfl П‡ЪВП‡ЪЛ˜ВТНУ„У П‡flЪМЛН‡ (1) Л Ы ‡‚МВМЛfl „‡ ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡ (2), fl‚Оfl˛˘В„УТfl В„У ОЛМВИМ˚П Ф Л·ОЛКВМЛВП? й‰МУ ЛБ Ф ЛМˆЛФЛ‡О¸М˚ı УЪОЛ˜ЛИ ТУТЪУЛЪ ‚ ТОВ‰Ы˛˘ВП. м ‡‚МВМЛ˛ „‡ ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡ ТУУЪ‚ВЪТЪ‚ЫВЪ ЛМЪВ„ ‡О ‰‚ЛКВМЛfl, ЛПВ˛˘ЛИ ТП˚ТО Б‡НУМ‡ ТУı ‡МВМЛfl ˝МВ „ЛЛ, ТОВ‰Ы˛- ˘В„У ‚Л‰‡:

„‰В ФВ ‚УВ ТО‡„‡ВПУВ ‚ Ф ‡‚УИ ˜‡ТЪЛ, Б‡‚ЛТfl˘ВВ УЪ ТНУ УТЪЛ ЛБПВМВМЛfl Ы„О‡, ВТЪ¸ НЛМВЪЛ˜ВТН‡fl ˝МВ „Лfl

= ω20θ2 ⁄ 2. е˚ ‚Л‰ЛП, ˜ЪУ ФУЪВМˆЛ‡О¸М‡fl ˝МВ „Лfl „‡ - ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡ Ф В‰ТЪ‡‚ОflВЪ ТУ·УИ Ф‡ ‡·У- ОЫ Л ЛПВВЪ У‰МЫ ˝НТЪ ВП‡О¸МЫ˛ ЪУ˜НЫ – ЪУ˜НЫ ПЛМЛПЫ- П‡ θ = 0 Л ТЪ ВПЛЪТfl Н ·ВТНУМВ˜МУТЪЛ Т УТЪУП θ.

СОfl Ы ‡‚МВМЛfl П‡ЪВП‡ЪЛ˜ВТНУ„У П‡flЪМЛН‡ НЛМВЪЛ- ˜ВТН‡fl ˝МВ „Лfl ЛПВВЪ ЪУЪ КВ Т‡П˚И ‚Л‰, ˜ЪУ Л ‰Оfl „‡ - ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡, ‡ ФУЪВМˆЛ‡О¸М‡fl ˝МВ „Лfl УЪОЛ˜‡ВЪТfl Л ЛПВВЪ ‚Л‰

и Л П‡О˚ı Ы„О‡ı УЪНОУМВМЛfl θ ! 1 ФУЪВМˆЛ‡О¸М‡fl ˝МВ - „Лfl П‡flЪМЛН‡ ·ОЛБН‡ Н ФУЪВМˆЛ‡О¸МУИ ˝МВ „ЛЛ УТˆЛООflЪУ ‡. й‰М‡НУ ‚ УЪОЛ˜ЛВ УЪ УТˆЛООflЪУ ‡ ФУЪВМˆЛ‡О¸М‡fl ˝МВ „Лfl П‡flЪМЛН‡ ЛПВВЪ МВ У‰МЫ, ‡ ·ВТНУМВ˜МУВ ˜ЛТОУ ЪУ˜ВН ПЛМЛПЫП‡, УФ В‰ВОflВП˚ı ЫТОУ‚ЛВП θn = 2πn, „‰Â n – ˆВОУВ ˜ЛТОУ. ЗУ-‚ЪУ ˚ı, ФУЪВМˆЛ‡О¸М‡fl ˝МВ „Лfl П‡flЪМЛН‡ У„ ‡МЛ˜ВМ‡ Л ‰УТЪЛ„‡ВЪ П‡НТЛПЫП‡ ‚ ЪУ˜Н‡ı θm = π(2m + 1), „‰Â m – ˆÂÎÓ ˜ËÒÎÓ.

щЪЛ УЪОЛ˜Лfl ‚ ‚Л‰В ФУЪВМˆЛ‡О¸МУИ ˝МВ „ЛЛ Ф Л‚У- ‰flЪ Н Ф ЛМˆЛФЛ‡О¸М˚П УЪОЛ˜ЛflП ‚ ‚Л‰В В¯ВМЛИ Ы ‡‚- МВМЛИ (1) Л (2). и Л ω20 > 0 Ы ‡‚МВМЛВ УТˆЛООflЪУ ‡ ЛПВВЪ В¯ВМЛВ ‚ ‚Л‰В „‡ ПУМЛ˜ВТНЛı МВБ‡ЪЫı‡˛˘Лı НУОВ·‡МЛИ. л ЩЛБЛ˜ВТНУИ ЪУ˜НЛ Б ВМЛfl ˝ЪЛ В¯ВМЛfl УФЛТ˚‚‡˛Ъ ФВ ЛУ‰Л˜ВТНЛВ Ф В‚ ‡˘ВМЛfl ФУЪВМˆЛ‡О¸- МУИ ˝МВ „ЛЛ УТˆЛООflЪУ ‡ ‚ НЛМВЪЛ˜ВТНЫ˛ ˝МВ „Л˛ В„У ‰‚ЛКВМЛfl Л У· ‡ЪМУ. лНУО¸ ·˚ МЛ ·˚О‡ ‚ВОЛН‡ М‡˜‡О¸- М‡fl НЛМВЪЛ˜ВТН‡fl ˝МВ „Лfl УТˆЛООflЪУ ‡, УМ ‚ТВ„‰‡ УТЪ‡- МУ‚ЛЪТfl Л В„У НЛМВЪЛ˜ВТН‡fl ˝МВ „Лfl ФУОМУТЪ¸˛ ФВ ВИ- ‰ВЪ ‚ ФУЪВМˆЛ‡О¸МЫ˛.

м ‡‚МВМЛВ П‡flЪМЛН‡ Ъ‡НКВ ЛПВВЪ УТˆЛООЛ Ы˛˘ЛВВ¯ВМЛfl. й‰М‡НУ, ‚У-ФВ ‚˚ı, ˝ЪЛ УТˆЛООflˆЛЛ МВ fl‚Оfl-

˛ЪТfl „‡ ПУМЛ˜ВТНЛПЛ. ЗУ-‚ЪУ ˚ı, ˝ЪЛ УТˆЛООЛ Ы˛- ˘ЛВ В¯ВМЛfl ·˚‚‡˛Ъ ‰‚Ыı ЪЛФУ‚. З ФВ ‚УП ТОЫ˜‡В, Ъ‡Н КВ Н‡Н Л ‰Оfl УТˆЛООflЪУ ‡, Ф УЛТıУ‰ЛЪ ФВ ЛУ‰Л˜ВТНУВ Ф ВУ· ‡БУ‚‡МЛВ НЛМВЪЛ˜ВТНУИ ˝МВ „ЛЛ ‚ ФУЪВМˆЛ‡О¸- МЫ˛ Л У· ‡ЪМУ. ЗУ ‚ЪУ УП МВ ‚Тfl НЛМВЪЛ˜ВТН‡fl ˝МВ „Лfl П‡flЪМЛН‡ ПУКВЪ ·˚Ъ¸ Ф ВУ· ‡БУ‚‡М‡ ‚ ФУЪВМˆЛ‡О¸МЫ˛. щЪУ Т‚flБ‡МУ Т ЪВП, ˜ЪУ П‡flЪМЛН ТУ‚В ¯‡ВЪ НУОВ·‡МЛfl ОЛ¯¸ ‚ У„ ‡МЛ˜ВММУИ У·О‡ТЪЛ Ф УТЪ ‡МТЪ‚‡, ФУ˝ЪУПЫ В„У ФУЪВМˆЛ‡О¸М‡fl ˝МВ „Лfl ЛПВВЪ МВ ЪУО¸НУ ПЛМЛП‡О¸- МУВ, МУ Л П‡НТЛП‡О¸МУВ БМ‡˜ВМЛВ.

з‡Л·УОВВ fl НУВ УЪОЛ˜ЛВ МВОЛМВИМУ„У Ы ‡‚МВМЛfl

(1) УЪ ОЛМВИМУ„У (2) ТУТЪУЛЪ, ФУК‡ОЫИ, ‚ ЪУП, ˜ЪУ М‡ fl- ‰Ы Т УТˆЛООЛ Ы˛˘ЛПЛ В¯ВМЛflПЛ Ы ‡‚МВМЛВ (1) ЛПВВЪ МВУТˆЛООЛ Ы˛˘ВВ В¯ВМЛВ, ‰Оfl НУЪУ У„У НЛМВЪЛ˜ВТ- Н‡fl ˝МВ „Лfl ТЪ ВПЛЪТfl Н МЫО˛ Ф Л ТЪ ВПОВМЛЛ ‚ ВПВМЛ Н ·ВТНУМВ˜МУТЪЛ (t ± ). щЪУ В¯ВМЛВ ТУУЪ‚ВЪТЪ‚Ы- ВЪ ТЛЪЫ‡ˆЛЛ, НУ„‰‡ ˜‡ТЪЛˆ‡ ТЪ‡ ЪЫВЪ Т ЪУ˜НЛ П‡НТЛПЫП‡ ФУЪВМˆЛ‡О¸МУИ ˝МВ „ЛЛ Л Б‡Н‡М˜Л‚‡ВЪ Т‚УВ ‰‚ЛКВМЛВ М‡ ТУТВ‰МВП П‡НТЛПЫПВ ФУЪВМˆЛ‡О¸МУИ ˝МВ „ЛЛ. йМУ ЛПВВЪ ‚Л‰

уВП УЪОЛ˜‡ВЪТfl ‡ФВ ЛУ‰Л˜ВТНУВ В¯ВМЛВ (3) УЪ ФВ-ЛУ‰Л˜ВТНЛı В¯ВМЛИ „‡ ПУМЛ˜ВТНУ„У УТˆЛООflЪУ ‡? СВОУ ‚ ЪУП, ˜ЪУ НЛМВЪЛ˜ВТНУИ Л ФУЪВМˆЛ‡О¸МУИ ˝МВ - „ЛЛ П‡flЪМЛН‡ (Н‡Н Л О˛·У„У ‰ Ы„У„У ЪВО‡) ПУКВЪ ·˚Ъ¸ Ф Л‰‡М ‡БОЛ˜М˚И ТП˚ТО. иУЪВМˆЛ‡О¸М‡fl ˝МВ „Лfl Т‚fl- Б‡М‡ Т ФУОУКВМЛВП ˜‡ТЪЛˆ˚ ‚ ФУОВ ТЛО ЪflКВТЪЛ, ‡ НЛМВЪЛ˜ВТН‡fl – ТУ ТНУ УТЪ¸˛ ВВ ФВ ВПВ˘ВМЛfl. д‡Н П˚ ‚Л- ‰ЛП, ‡‚МУ‚ВТЛВ (‚ ТП˚ТОВ ТУı ‡МВМЛfl ФУОМУИ ˝МВ „ЛЛ) ‚ ОЛМВИМУП ПЛ В ПУКВЪ УТЫ˘ВТЪ‚ОflЪ¸Тfl ФЫЪВП ФВ ЛУ- ‰Л˜ВТНУ„У Ф ВУ· ‡БУ‚‡МЛfl НЛМВЪЛ˜ВТНУИ ˝МВ „ЛЛ ‚ ФУЪВМˆЛ‡О¸МЫ˛ Л У· ‡ЪМУ. З МВОЛМВИМУП ПЛ В ‡‚МУ‚В- ТЛВ ПУКВЪ ‰УТЪЛ„‡Ъ¸Тfl Н‡Н ФВ ЛУ‰Л˜ВТНЛП У·ПВМУП, Ъ‡Н Л ТЪ У„У ОУН‡ОЛБУ‚‡ММ˚П ‚У ‚ ВПВМЛ У·ПВМУП ˝МВ „ЛЛ. е˚ ‚Л‰ЛП ЛБ (3), ˜ЪУ ı‡ ‡НЪВ М‡fl ‰ОЛЪВО¸- МУТЪ¸ Ф УˆВТТ‡ У·ПВМ‡ ˝МВ „ЛВИ t0 = 1/ω0 .

кЦбйзАзлзйЦ ЗбАаейСЦвлнЗаЦ лЗЦнА л ЗЦфЦлнЗйе

иЫТЪ¸ ЪВФВ ¸ Ы М‡Т ЛПВВЪТfl МВ У‰ЛМ П‡flЪМЛН, ‡ М‡·У Т‚flБ‡ММ˚ı П‡flЪМЛНУ‚. л‚flБ¸ П‡flЪМЛНУ‚ ПУКВЪ УТЫ- ˘ВТЪ‚ОflЪ¸Тfl, М‡Ф ЛПВ , Т ФУПУ˘¸˛ Ф ЫКЛМУН, ТУ- В‰ЛМfl˛˘Лı УЪ‰ВО¸М˚В П‡flЪМЛНЛ, ЛОЛ КВ Т ФУПУ˘¸˛ ˝ОВНЪ УП‡„МЛЪМ˚ı ФУОВИ, ВТОЛ „ ЫБЛНЛ П‡flЪМЛНУ‚ ˝ОВНЪ Л˜ВТНЛ Б‡ flКВМ˚ ЛОЛ fl‚Оfl˛ЪТfl П‡„МЛЪ‡ПЛ. З Ъ‡НУИ ТЛТЪВПВ НУОВ·‡МЛВ О˛·У„У ЛБ П‡flЪМЛНУ‚ Ф Л‚В- ‰ВЪ Н НУОВ·‡МЛflП В„У ТУТВ‰ВИ, ‡ ТОВ‰У‚‡ЪВО¸МУ, ‚ ТЛТЪВПВ ‚УБМЛНМВЪ ‚УОМ‡ ‚УБ·ЫК‰ВМЛfl НУОВ·‡МЛИ, ‡ТФ УТЪ-‡Мfl˛˘‡flТfl ФУ ТЛТЪВПВ Т НУМВ˜МУИ ТНУ УТЪ¸˛. н‡Н КВ Н‡Н Л ‚ ТОЫ˜‡В НУОВ·‡ЪВО¸М˚ı Ф УˆВТТУ‚, ‚УОМУ‚˚В Ф УˆВТТ˚ ПУ„ЫЪ ·˚Ъ¸ ОЛМВИМ˚ПЛ ЛОЛ МВОЛМВИМ˚ПЛ.

к‡БМУУ· ‡БМ˚В Ф ЛПВ ˚ ОЛМВИМ˚ı Л МВОЛМВИМ˚ı ‚УОМУ‚˚ı Ф УˆВТТУ‚ У·ТЫК‰‡ОЛТ¸ М‡ ТЪ ‡МЛˆ‡ı “лУ УТУ‚- ТНУ„У й· ‡БУ‚‡ЪВО¸МУ„У ЬЫ М‡О‡” ‚ [1, 2]. З ˝ЪЛı ТЪ‡Ъ¸- flı ·˚ОУ УЪПВ˜ВМУ, ˜ЪУ У‰МЛП ЛБ М‡Л·УОВВ ЛМЪВ ВТМ˚ı Л ‚‡КМ˚ı МВОЛМВИМ˚ı ‚УОМУ‚˚ı Ф УˆВТТУ‚ fl‚ОflВЪТfl ˜‡Т- ЪЛˆВФУ‰У·МУВ, ЛОЛ ТУОЛЪУММУВ, ‡ТФ УТЪ ‡МВМЛВ ‚УОМ, НУ„‰‡ ‚УОМ‡ ‚УБ·ЫК‰ВМЛfl ‰‚ЛКВЪТfl ФУ ТЛТЪВПВ ‚ ‚Л‰В ЫВ‰ЛМВММУ„У ЛПФЫО¸Т‡, ЩУ П‡ НУЪУ У„У МВ ПВМflВЪТfl ФУ ПВ В ‡ТФ УТЪ ‡МВМЛfl. н‡НУВ ФУ‚В‰ВМЛВ ‰ВИТЪ‚ЛЪВО¸МУ МВУ·˚˜МУ. ЕУОВВ ВТЪВТЪ‚ВММ˚П Н‡КВЪТfl Ф УˆВТТ, НУ„‰‡ ‚УБ·ЫК‰ВМЛВ У‰МУ„У ЛБ П‡flЪМЛНУ‚ ФВ В‰‡ВЪТfl ‚ТВ ·УО¸- ¯ВПЫ Лı ˜ЛТОЫ. З ˝ЪУП ТОЫ˜‡В ‡ПФОЛЪЫ‰‡ НУОВ·‡МЛИ Н‡К‰У„У ЛБ П‡flЪМЛНУ‚ ФУТЪВФВММУ ЫПВМ¸¯‡ВЪТfl, ФУТНУО¸НЫ ФУЪВМˆЛ‡О¸М‡fl ЛОЛ НЛМВЪЛ˜ВТН‡fl ˝МВ „Лfl ‚УБ- ·ЫК‰ВМЛfl У‰МУ„У ЛБ П‡flЪМЛНУ‚ ФУТЪВФВММУ ФВ В ‡Т- Ф В‰ВОflВЪТfl ПВК‰Ы ‚ТВ ·УО¸¯ЛП Лı ˜ЛТОУП.

З ЫФУПflМЫЪ˚ı ТЪ‡Ъ¸flı ·˚ОЛ Ф Л‚В‰ВМ˚ Ф ЛПВ ˚ ‚УБМЛНМУ‚ВМЛfl ЫВ‰ЛМВММ˚ı ‚УОМ ‚ ‡БМУУ· ‡БМ˚ı ЩЛБЛ˜ВТНЛı Ф УˆВТТ‡ı. е˚ УТЪ‡МУ‚ЛПТfl Б‰ВТ¸ ОЛ¯¸ М‡ У‰МУП ЛБ Ъ‡НЛı Ф ЛПВ У‚ – ТУОЛЪУМ‡ı Т‡ПУЛМ‰ЫˆЛ У- ‚‡ММУИ Ф УБ ‡˜МУТЪЛ, ‚УБМЛН‡˛˘Лı ‚ Ф УˆВТТВ ‡Т- Ф УТЪ ‡МВМЛfl ЛПФЫО¸Т‡ НУ„В ВМЪМУ„У Т‚ВЪ‡ ‚ ТЛТЪВПВВБУМ‡МТМ˚ı ‡ЪУПУ‚, Л У·ТЫ‰ЛП ОЛ¯¸ У‰ЛМ ЛБ ‡ТФВНЪУ‚ У·˘ВИ Ф У·ОВП˚, Т‚flБ‡ММ˚И ТУ ТНУ УТЪ¸˛ ‡ТФ УТЪ ‡- МВМЛfl ТУОЛЪУМУ‚. щЪУЪ Ф ЛПВ Ф Л‚ОВН‡ЪВОВМ ЪВП, ˜ЪУ Ы ‡‚МВМЛВ, УФЛТ˚‚‡˛˘ВВ ‡ТФ УТЪ ‡МВМЛВ НУ„В ВМЪМУ„У ЛПФЫО¸Т‡ Т‚ВЪ‡ ‚ Т В‰В ВБУМ‡МТМ˚ı ‡ЪУПУ‚, ·ОЛБНУ Н Ы ‡‚МВМЛ˛ П‡ЪВП‡ЪЛ˜ВТНУ„У П‡flЪМЛН‡ Л ЛПВВЪ ‚Л‰

е˚ ‚Л‰ЛП, ˜ЪУ ‚ УЪОЛ˜ЛВ УЪ НУОВ·‡ЪВО¸МУ„У Ф УˆВТТ‡ Ы ‡‚МВМЛВ ‚УОМУ‚У„У Ф УˆВТТ‡ ‚НО˛˜‡ВЪ МВ ЪУО¸НУ ‚ В- Пfl t, ÌÓ Ë Ô ÓÒÚ ‡ÌÒÚ‚ÂÌÌÛ˛ ÍÓÓ ‰Ë̇ÚÛ ı, ‡ Ú‡ÍÊ ه- ÁÓ‚Û˛ ÒÍÓ ÓÒÚ¸ ‡ÒÔ ÓÒÚ ‡ÌÂÌËfl Ò‚ÂÚ‡ ‚ Ò Â‰Â Ò.

СОfl ЪУ„У ˜ЪУ·˚ ФУflТМЛЪ¸ ТП˚ТО ФВ ВПВММ˚ı, ‚ıУ- ‰fl˘Лı ‚ Ы ‡‚МВМЛВ (4), У·ТЫ‰ЛП ФУ‰ У·МВВ ЩЛБЛНЫ Т‡- ПУ„У Ф УˆВТТ‡. пУ У¯У ЛБ‚ВТЪМУ, ˜ЪУ ЩЛБЛН‡ ‡ЪУПУ‚ Л ПУОВНЫО fl‚ОflВЪТfl ЩЛБЛНУИ Н‚‡МЪУ‚˚ı ТЛТЪВП. щМВ „Лfl ˝ОВНЪ УМ‡ ‚ ‡ЪУПВ МВ ПУКВЪ ЛБПВМflЪ¸Тfl МВФ В ˚‚МУ, ‡ Ф ЛМЛП‡ВЪ ОЛ¯¸ ‰ЛТН ВЪМ˚В БМ‡˜ВМЛfl. З УТМУ‚МУП (МВ‚УБ·ЫК‰ВММУП) ТУТЪУflМЛЛ ‡ЪУП‡ В„У ˝ОВНЪ УМ˚ Б‡- МЛП‡˛Ъ ТУТЪУflМЛfl Т М‡ЛПВМ¸¯ВИ ˝МВ „ЛВИ. и Л ‚Б‡Л- ПУ‰ВИТЪ‚ЛЛ ‡ЪУП‡ Т ˝ОВНЪ УП‡„МЛЪМУИ ‚УОМУИ ˝ОВН- Ъ УМ˚ ПУ„ЫЪ ФВ ВıУ‰ЛЪ¸ ‚ ‚УБ·ЫК‰ВММ˚В ТУТЪУflМЛfl Т ·УО¸¯ВИ ˝МВ „ЛВИ. иЫТЪ¸ Ö1 – ˝МВ „Лfl ‚‡ОВМЪМУ„У ˝ОВН- Ъ УМ‡ ‡ЪУП‡ ‚ УТМУ‚МУП ТУТЪУflМЛЛ, ‡ Ö2 – ‚ ‚УБ·ЫК‰ВММУП. и УˆВТТ ‚УБ·ЫК‰ВМЛfl ‡ЪУП‡ М‡Л·УОВВ ˝ЩЩВНЪЛ- ‚ВМ ‚ ЪУП ТОЫ˜‡В, НУ„‰‡ ˝МВ „Лfl Н‚‡МЪ‡ ФУОfl "ω0 ТУ‚Ф‡‰‡ВЪ Т ‡БМУТЪ¸˛ ˝МВ „ЛИ УТМУ‚МУ„У Л ‚УБ·ЫК- ‰ВММУ„У ТУТЪУflМЛИ Ö2 − Ö1 = "ω0 . Ç ˝ÚÓÏ ÒÎÛ˜‡Â, ÔÓ„ÎÓÚË‚ Í‚‡ÌÚ Ò‚ÂÚ‡, ‡ÚÓÏ Á‡‚‰ÓÏÓ Ó͇ÊÂÚÒfl ‚ ‚ÓÁ·ÛʉÂÌ-

МУП ТУТЪУflМЛЛ Т ˝МВ „ЛВИ Ö2 , ‡ МВ ‚ Н‡НУП ОЛ·У ‰ Ы„УП ‚УБ·ЫК‰ВММУП ТУТЪУflМЛЛ. лОВ‰У‚‡ЪВО¸МУ, Ф Л ВБУ- М‡МТМУП ‚Б‡ЛПУ‰ВИТЪ‚ЛЛ Т‚ВЪ‡ Т ‚В˘ВТЪ‚УП П˚ ПУКВП ФУО‡„‡Ъ¸, ˜ЪУ ‡ЪУП fl‚ОflВЪТfl ‰‚ЫıЫ У‚МВ‚˚П. иЫТЪ¸ ‚ У·˙ВПВ V Т В‰˚ ЛПВВЪТfl N ‰‚ЫıЫ У‚МВ‚˚ı ‡ЪУПУ‚ Л ФЫТЪ¸ ‚ ПУПВМЪ ‚ ВПВМЛ t ‚ ‚УБ·ЫК‰ВММУП ТУТЪУflМЛЛ М‡ıУ‰flЪТfl N2(t) ‡ÚÓÏÓ‚, ‡ N1(t) – ‚ УТМУ‚МУП. З ˝ЪУП ТУТЪУflМЛЛ ТЛТЪВП‡ ‡ЪУПУ‚ ЛПВВЪ ˝МВ „Л˛

E(t) = E2 N2(t) + E1 N1(t) =

м˜ЛЪ˚‚‡fl, ˜ЪУ ФУОМУВ ˜ЛТОУ ‡ЪУПУ‚ ‚ ТЛТЪВПВ УТЪ‡ВЪТfl МВЛБПВММ˚П, N2(t) + N1(t) = N, П˚ ‚Л‰ЛП, ˜ЪУ ФУТОВ‰- МВВ ТО‡„‡ВПУВ ‚ ˝ЪУП ‚˚ ‡КВМЛЛ УЪ ‚ ВПВМЛ МВ Б‡‚ЛТЛЪ, ФУ˝ЪУПЫ П˚ ‚ТВ„‰‡ ПУКВП ФУОУКЛЪ¸ E2 + E1 = 0. щЪУ ˝Н- ‚Л‚‡ОВМЪМУ ЪУПЫ, ˜ЪУ ФУЪВМˆЛ‡О¸МЫ˛ ˝МВ „Л˛ П‡flЪМЛ- Н‡ П˚ УЪТ˜ЛЪ˚‚‡ВП УЪ ЪУ˜НЛ ФУ‰‚ВТ‡, ‚ ˝ЪУП ТОЫ˜‡В ФУЪВМˆЛ‡О¸М‡fl ˝МВ „Лfl П‡flЪМЛН‡ ‚ ЪУ˜НВ ЫТЪУИ˜Л‚У„У‡‚МУ‚ВТЛfl ‡‚М‡ Π1 = −mgl, ‡ ‚ ЪУ˜НВ МВЫТЪУИ˜Л‚У„У‡‚МУ‚ВТЛfl Π2 = mgl. н‡НЛП У· ‡БУП, ˝МВ „Лfl ‡ЪУПМУИ ТЛТЪВП˚ ‚ ПУПВМЪ ‚ ВПВМЛ t Ф УФУ ˆЛУМ‡О¸М‡ ‡БМУТЪЛ М‡ТВОВММУТЪВИ Ы У‚МВИ N2(t) − N1(t). ЦТОЛ ЛПВЪ¸ ‰ВОУ Т Ф УЪflКВММУИ Т В‰УИ ‡ЪУПУ‚, ЪУ ˜ЛТОУ ‡ЪУПУ‚ N2(x, t) ‚ ‚УБ·ЫК‰ВММУП ТУТЪУflМЛЛ ‚ ‡БОЛ˜М˚ı ЪУ˜Н‡ı ı Ó·˙Âχ V ‚ У‰ЛМ Л ЪУЪ КВ ПУПВМЪ ‚ ВПВМЛ t ПУКВЪ ·˚Ъ¸‡БОЛ˜МУ. ЕУОВВ ЪУ„У, ФОУЪМУТЪ¸ ˜ЛТО‡ ‡ЪУПУ‚ n(x) = = N(x)/ V ПУКВЪ ·˚Ъ¸ МВУ‰ЛМ‡НУ‚‡ ‚ ‡БОЛ˜М˚ı Ф У- ТЪ ‡МТЪ‚ВММ˚ı ЪУ˜Н‡ı, ВТОЛ У· ‡БВˆ МВУ‰МУ У‰ВМ, ФУ- ˝ЪУПЫ ‚ПВТЪУ ˝МВ „ЛЛ ‡ЪУПМУИ ФУ‰ТЛТЪВП˚ Ы‰У·МВВ ‚‚ВТЪЛ ФОУЪМУТЪ¸ ˝МВ „ЛЛ e(x, t) Ë Ô Â‰ÒÚ‡‚ËÚ¸  ‚ ‚ˉÂ

( , ) N "ω0 ( ) θ( , ) e x t ------------- R0 x cos x t .

= 2V

н‡НЛП У· ‡БУП, ФВ ВПВММ‡fl θ(x, t), ЩЛ„Ы Л Ы˛˘‡fl ‚ Ы ‡‚МВМЛЛ (4), УФ В‰ВОflВЪ ФОУЪМУТЪ¸ ˝МВ „ЛЛ ‡ЪУПМУИ ТЛТЪВП˚ ‡М‡ОУ„Л˜МУ ЪУПЫ, Н‡Н Ы„УО θ УФ В‰ВОflВЪ ФУЪВМˆЛ‡О¸МЫ˛ ˝МВ „Л˛ П‡flЪМЛН‡. щЪ‡ ФВ ВПВММ‡fl ‚ ЪВУ ЛЛ ‰‚ЫıЫ У‚МВ‚У„У ‡ЪУП‡ ФУОЫ˜ЛО‡ М‡Б‚‡МЛВ Ы„О‡ ЕОУı‡.

СУ ТЛı ФУ П˚ ‰У„У‚У ЛОЛТ¸ ОЛ¯¸ У ЪУ˜НВ М‡˜‡О‡ УЪТ˜ВЪ‡ ˝МВ „ЛЛ ‡ЪУП‡, МУ МВ У М‡Ф ‡‚ОВМЛЛ ˝МВ „ВЪЛ- ˜ВТНУИ УТЛ. ЕЫ‰ВП Т˜ЛЪ‡Ъ¸, ˜ЪУ ‰У Ф ЛıУ‰‡ ‚ ЪУ˜НЫ ı ЛПФЫО¸Т‡ Т‚ВЪ‡ Ы„УО ЕОУı‡ θ(x, t) ‚Ò„‰‡ ‡‚ÂÌ ÌÛβ, ÚÓ„‰‡‡‚ÂÌÒÚ‚Ó R0(x) = −1 УБМ‡˜‡ВЪ, ˜ЪУ ‚ М‡˜‡О¸М˚И ПУПВМЪ ‚ ВПВМЛ ‚ТВ ‡ЪУП˚ ·˚ОЛ ‚ УТМУ‚МУП ТУТЪУflМЛЛ Т ˝МВ - „ЛВИ E1 = −"ω0 /2 Л ФОУЪМУТЪ¸ ‡ЪУПУ‚ ‚‰УО¸ М‡Ф ‡‚ОВМЛfl ‡ТФ УТЪ ‡МВМЛfl ‚УОМ˚ МВ ПВМflВЪТfl. ЦТОЛ ФОУЪМУТЪ¸ ‡ЪУПУ‚ МВ fl‚ОflВЪТfl ФУТЪУflММУИ, ЪУ R0(x) Á‡‚ËÒËÚ ÓÚ ı. з‡Ф ЛПВ , ВТОЛ Т В‰‡ ЛПВВЪ ‡БПВ L ‚‰Óθ ÓÒË ı Л ФОУЪМУТЪ¸ ‡ЪУПУ‚ ‚ У·˙ВПВ ФУТЪУflММ‡, ЪУ R0(x) = −1 Ô Ë x [0, L] Ë ‡‚̇ ÌÛβ ‚Ì Û͇Á‡ÌÌÓ„Ó ËÌÚ ‚‡Î‡.

ЦТОЛ ‡ЪУП˚ ‰У Ф ЛıУ‰‡ ЛПФЫО¸Т‡ Т‚ВЪ‡ М‡ıУ‰flЪТfl ‚ ‚УБ- ·ЫК‰ВММУП ТУТЪУflМЛЛ, ЪУ R0(x) = 1.

ЗБ‡ЛПУ‰ВИТЪ‚ЛВ Т‚ВЪ‡ Т ‡ЪУПМУИ ТЛТЪВПУИ ТУТЪУЛЪ ‚ ЪУП, ˜ЪУ, ФУ„ОУ˘‡fl Н‚‡МЪ Т‚ВЪ‡, У‰ЛМ ЛБ ‡ЪУПУ‚ ТЛТЪВ- П˚ ФВ ВıУ‰ЛЪ ЛБ УТМУ‚МУ„У ТУТЪУflМЛfl ‚ ‚УБ·ЫК‰ВММУВ, Ф Л ˝ЪУП N2 Û‚Â΢˂‡ÂÚÒfl ̇ ‰ËÌ˘ÍÛ, ‡ N1 ЫПВМ¸¯‡- ВЪТfl. й· ‡ЪМ˚И Ф УˆВТТ ФВ ВıУ‰‡ ‡ЪУП‡ ЛБ ‚УБ·ЫК‰ВММУ„У ТУТЪУflМЛfl ‚ УТМУ‚МУВ Ф Л‚У‰ЛЪ Н УК‰ВМЛ˛ Н‚‡М- Ъ‡ Т‚ВЪ‡. зВТОУКМУ ‰У„‡‰‡Ъ¸Тfl, ˜ЪУ ‡ПФОЛЪЫ‰‡ Т‚ВЪУ‚УИ ‚УОМ˚ ·Ы‰ВЪ Ф УФУ ˆЛУМ‡О¸М‡ Ф УЛБ‚У‰МУИ ФУ ‚ ВПВ-

дУ˝ЩЩЛˆЛВМЪ Ф УФУ ˆЛУМ‡О¸МУТЪЛ Б‡‚ЛТЛЪ УЪ Ф‡ ‡- ПВЪ ‡ β, ‚‚В‰ВММУ„У М‡ПЛ ‡МВВ ‚ Ы ‡‚МВМЛВ (4). и‡ ‡- ПВЪ β Б‡‚ЛТЛЪ УЪ Т‚УИТЪ‚ Т В‰˚ Л, Н‡Н ПУКМУ ‚Л‰ВЪ¸ ЛБ (4), ЛПВВЪ ‡БПВ МУТЪ¸ Н‚‡‰ ‡Ъ‡ ˜‡ТЪУЪ˚ НУОВ·‡МЛИ.

лйганйзх

м ‡‚МВМЛВ (4) ПУКМУ Т‚ВТЪЛ Н Ы ‡‚МВМЛ˛ П‡ЪВП‡ЪЛ˜В- ТНУ„У П‡flЪМЛН‡ ‚ ‰‚Ыı ТОЫ˜‡flı. ЗУ-ФВ ‚˚ı, НУ„‰‡ θ(x, t) Ì Á‡‚ËÒËÚ ÓÚ ı. щЪУЪ ТОЫ˜‡И ТУУЪ‚ВЪТЪ‚ЫВЪ ЪУПЫ, ˜ЪУ ‡ЪУП˚ ‚Б‡ЛПУ‰ВИТЪ‚Ы˛Ъ Т ФОУТНУИ ‚УОМУИ, ‡ПФОЛЪЫ‰‡ НУЪУ УИ У‰ЛМ‡НУ‚‡ ‚У ‚ТВı ЪУ˜Н‡ı Т В‰˚ Л ЛБПВМflВЪТfl ‚У ‚ ВПВМЛ ‚ ВБЫО¸Ъ‡ЪВ Ф УˆВТТУ‚ ВБУМ‡МТМУ„У ФУ- „ОУ˘ВМЛfl Л ЛТФЫТН‡МЛfl Н‚‡МЪУ‚ Т‚ВЪ‡ ‡ЪУП‡ПЛ.

ЗЪУ УИ ТОЫ˜‡И ·УОВВ ЛМЪВ ВТВМ Л ТУУЪ‚ВЪТЪ‚ЫВЪ Т‡- ПУТУ„О‡ТУ‚‡ММУПЫ ‡ТФ УТЪ ‡МВМЛ˛ ЛПФЫО¸Т‡. и Л Т‡- ПУТУ„О‡ТУ‚‡ММУП ‡ТФ УТЪ ‡МВМЛЛ ЛПФЫО¸Т‡ В„У ‚ В- ПВММУИ Ф УЩЛО¸ У‰ЛМ‡НУ‚ ‚У ‚ТВı ЪУ˜Н‡ı ı Т Ы˜ВЪУП ‚ ВПВМЛ Б‡Ф‡Б‰˚‚‡МЛfl, МВУ·ıУ‰ЛПУ„У ‰Оfl ЪУ„У, ˜ЪУ·˚ ЛПФЫО¸Т ПУ„ ФВ ВПВТЪЛЪ¸Тfl ЛБ У‰МУИ ЪУ˜НЛ М‡·О˛‰В- МЛfl ‚ ‰ Ы„Ы˛. З ˝ЪУП ТОЫ˜‡В ‡ПФОЛЪЫ‰‡ ФУОfl a(x, t) ËÎË Û„ÓÎ θ(x, t) Б‡‚ЛТflЪ ОЛ¯¸ УЪ Б‡Ф‡Б‰˚‚‡˛˘В„У ‚ ВПВМЛ τ = t − x/ν, „‰В ν – ТНУ УТЪ¸ ‡ТФ УТЪ ‡МВМЛfl ЛПФЫО¸Т‡. у‡ТЪМ˚П ТОЫ˜‡ВП Т‡ПУТУ„О‡ТУ‚‡ММУ„У ‡ТФ УТЪ ‡МВМЛfl fl‚ОflВЪТfl ТУОЛЪУММУВ ‡ТФ УТЪ ‡МВМЛВ ‚ ‚Л‰В ЫВ‰Л- МВММУ„У ЛПФЫО¸Т‡, НУ„‰‡ ‡ПФОЛЪЫ‰‡ ФУОfl ТЪ ВПЛЪТfl Н МЫО˛ Ф Л τ ± .

ǂ‰ÂÏ ·ÂÁ ‡ÁÏ Ì˚ ‚ ÂÏfl t' = t/T Ë ÍÓÓ ‰Ë̇ÚÛ x' = x/l, „‰Â l = T c, ‡ í – ÌÓ ÏË Ó‚Ó˜ÌÓ ‚ ÂÏfl. Ç ˝ÚÓÏ ÒÎÛ˜‡Â ·ÂÁ ‡ÁÏ Ì˚ÏË ÒÚ‡ÌÛÚ Ô‡ ‡ÏÂÚ β' = β τ2 Л ТНУ-УТЪ¸ ‡ТФ УТЪ ‡МВМЛfl ЛПФЫО¸Т‡ ν' = ν/c. С‡ОВВ ¯Ъ ЛıЛ ‰Оfl Н ‡ЪНУТЪЛ П˚ ·Ы‰ВП УФЫТН‡Ъ¸, ФУ˝ЪУПЫ ‡‚ВМТЪ‚У ν = 1 УБМ‡˜‡ВЪ, ˜ЪУ ТНУ УТЪ¸ ‡ТФ УТЪ ‡МВМЛfl ЛПФЫО¸Т‡‡‚М‡ ТНУ УТЪЛ Т‚ВЪ‡. иУО‡„‡fl θ(x, t) = θ(t − x/ν), ПУКМУ Т‚ВТЪЛ Ы ‡‚МВМЛВ (4) Н Ы ‡‚МВМЛ˛ (1), ‚ НУЪУ УП ˜‡-

‰ËÏ, ˜ÚÓ ˜‡ÒÚÓÚ‡ Ω fl‚ÎflÂÚÒfl ‰ÂÈÒÚ‚ËÚÂθÌÓÈ ‚Â΢ËÌÓÈ ‚ ‰‚Ûı ÒÎÛ˜‡flı: ‡) R0 < 0 Ë ν < 1; ·) R0 > 0 Ë ν > 1.

иВ ‚˚И ТОЫ˜‡И ТУУЪ‚ВЪТЪ‚ЫВЪ ТЛЪЫ‡ˆЛЛ, НУ„‰‡ М‡ ЛБМ‡˜‡О¸МУ МВ‚УБ·ЫК‰ВММЫ˛ Т В‰Ы Ф‡‰‡ВЪ ЛПФЫО¸Т ˝ОВНЪ УП‡„МЛЪМУ„У ЛБОЫ˜ВМЛfl Л Т‡ПУТУ„О‡ТУ‚‡ММУВ В„У‡ТФ УТЪ ‡МВМЛВ Ф УЛТıУ‰ЛЪ ТУ ТНУ УТЪ¸˛, ПВМ¸¯ВИ ТНУ УТЪЛ Т‚ВЪ‡. мВ‰ЛМВММУПЫ ЛПФЫО¸ТЫ ТУУЪ‚ВЪТЪ‚ЫВЪ ФУОЫ˜ВММУВ М‡ПЛ ‡МВВ В¯ВМЛВ (3) Ы ‡‚МВМЛfl П‡ЪВП‡- ЪЛ˜ВТНУ„У П‡flЪМЛН‡

и УЛБ‚В‰ВМЛВ ‡ПФОЛЪЫ‰˚ Л ‰ОЛЪВО¸МУТЪЛ Б‡‚ЛТЛЪ ОЛ¯¸ УЪ Ф‡ ‡ПВЪ ‡ β:

З ВБЫО¸Ъ‡ЪВ ˜В„У ФУТОВ Ф УıУК‰ВМЛfl ЛПФЫО¸Т‡ Ы„УО θ(x, t) Ô ËÌËχÂÚ Á̇˜ÂÌËÂ

+∞

θ(x, t = ∞) = β ∫ a(x, t')dt' = 2π.

–∞

щЪУ УБМ‡˜‡ВЪ, ˜ЪУ, ТЪ‡ ЪЫfl ЛБ МВ‚УБ·ЫК‰ВММУ„У ТУТЪУflМЛfl, ‡ЪУП˚ Т В‰˚ Н ТВ В‰ЛМВ ЛПФЫО¸Т‡ θ(τ = 0) = π ФВ ВıУ‰flЪ ‚ ‚УБ·ЫК‰ВММУВ ТУТЪУflМЛВ, ‡ ФУ В„У УНУМ˜‡- МЛЛ ТМУ‚‡ УН‡Б˚‚‡˛ЪТfl ‚ УТМУ‚МУП ТУТЪУflМЛЛ. аБ (5) П˚ ‚Л‰ЛП, ˜ЪУ ‚ Ф УЪflКВММУИ Т В‰В МВОЛМВИМ˚В ‚Б‡Л- ПУ‰ВИТЪ‚Лfl Ф Л‚У‰flЪ Н ФУfl‚ОВМЛ˛ ‚УБ·ЫК‰ВМЛИ ФУОfl, ОУН‡ОЛБУ‚‡ММ˚ı Н‡Н ‚ Ф УТЪ ‡МТЪ‚В, Ъ‡Н Л ‚У ‚ ВПВМЛ.

лУУЪМУ¯ВМЛВ (6), УФ В‰ВОfl˛˘ВВ Т‚flБ¸ ПВК‰Ы ‰ОЛЪВО¸МУТЪ¸˛ Л ТНУ УТЪ¸˛ ЛПФЫО¸Т‡, ПУКВЪ ·˚Ъ¸ У· ‡- ˘ВМУ Л Б‡ФЛТ‡МУ ‚ ‚Л‰В

Й ‡ЩЛН ˝ЪУИ Б‡‚ЛТЛПУТЪЛ ФУН‡Б‡М М‡ ЛТ. 1, ‡. е˚ ‚Л- ‰ЛП, ˜ЪУ ТНУ УТЪ¸ ЛПФЫО¸Т‡ Т ЫПВМ¸¯ВМЛВП В„У ‰ОЛЪВО¸- МУТЪЛ ТЪ ВПЛЪТfl Н ТНУ УТЪЛ Т‚ВЪ‡, УТЪ‡‚‡flТ¸ ПВМ¸¯В ВВ. мПВМ¸¯ВМЛВ ‰ОЛЪВО¸МУТЪЛ ЛПФЫО¸Т‡ ТУФ У‚УК‰‡ВЪТflУТЪУП В„У ‡ПФОЛЪЫ‰˚.

èÓÎÛ˜ÂÌÌ˚ ¯ÂÌËfl ÏÓ„ÛÚ ·˚Ú¸ ÙÓ Ï‡Î¸ÌÓ Ó·Ó·- ˘ÂÌ˚ ̇ ÒÎÛ˜‡È ËÁ̇˜‡Î¸ÌÓ ‚ÓÁ·ÛʉÂÌÌ˚ı Ò Â‰. ä‡Í

Ï˚ ÓÚϘ‡ÎË ‚˚¯Â, ‚Â΢Ë̇ Ω = βR0ν ⁄ (ν –1) =

= βν ⁄ (1 –ν) = 1 ⁄ τ0 ÓÒÚ‡ÂÚÒfl ‰ÂÈÒÚ‚ËÚÂθÌÓÈ Ë ‚ ÒÎÛ- ˜‡Â R0 > 0, ВТОЛ ФУОУКЛЪ¸, ˜ЪУ ТНУ УТЪ¸ ‡ТФ УТЪ ‡МВМЛfl ЛПФЫО¸Т‡ ТЪ‡МУ‚ЛЪТfl ·УО¸¯В ТНУ УТЪЛ Т‚ВЪ‡, ν > 1. и Л ˝ЪУП ЩУ ПЫО‡ (5) ТУı ‡МflВЪ Т‚УИ ‚Л‰, ‡ ‚ ЩУ ПЫО‡ı

v

1,0

‡

0,5

êËÒ. 1. ᇂЛТЛПУТЪ¸ ТНУ УТЪЛ ‡ТФ УТЪ ‡МВМЛfl ТУОЛЪУМ‡ υ УЪ В„У ‰ОЛЪВО¸МУТЪЛ τ0 ‰Îfl ÂÁÓ̇ÌÒÌÓ ÔÓ- „ÎÓ˘‡˛˘ÂÈ (‡) Л ЫТЛОЛ‚‡˛˘ВИ (·) Ò Â‰

(6) МЫКМУ Б‡ПВМЛЪ¸ 1 − ν М‡ ν − 1. й‰М‡НУ Ф Л ˝ЪУП Ф Л- МЛП‡ВЪ МВУ·˚˜М˚И ‚Л‰ Б‡‚ЛТЛПУТЪ¸ ТНУ УТЪЛ ЛПФЫО¸- Т‡ УЪ В„У ‰ОЛЪВО¸МУТЪЛ (‚ БМ‡ПВМ‡ЪВОВ ЩУ ПЫО˚ (7) БМ‡Н ФО˛Т МЫКМУ Б‡ПВМЛЪ¸ М‡ ПЛМЫТ). щЪ‡ Б‡‚ЛТЛПУТЪ¸ ФУ- Н‡Б‡М‡ М‡ ЛТ. 1, ·. å˚ ‚ˉËÏ, ˜ÚÓ Ô Ë τ0 # β−1/2 ÒÍÓ-ÓÒÚ¸ ·Óθ¯Â ÒÍÓ ÓÒÚË Ò‚ÂÚ‡, ‡ Ô Ë τ0 > β−1/2 ТНУ УТЪ¸ УЪ Лˆ‡ЪВО¸М‡. а ЪУ Л ‰ Ы„УВ ‚ıУ‰ЛЪ ‚ Ф УЪЛ‚У В˜ЛВ ТУ ТОУКЛ‚¯ЛПЛТfl Ф В‰ТЪ‡‚ОВМЛflПЛ. й‰М‡НУ УЪПВЪЛП, ˜ЪУ ‚ТВ Ф Л‚В‰ВММ˚В ‚˚¯В ‡ТТЫК‰ВМЛfl УЪМУТflЪТfl Н Т В‰‡П ·ВТНУМВ˜МУИ Ф УЪflКВММУТЪЛ. иУТНУО¸НЫ ‡ЪУП˚ М‡ıУ‰flЪТfl ‚ ‚УБ·ЫК‰ВММУП ТУТЪУflМЛЛ, ЪУ ˝ЪУ УБМ‡˜‡ВЪ, ˜ЪУ ˝МВ „Лfl ‚УБ·ЫК‰ВМЛfl ‡ЪУПМУИ ТЛТЪВП˚ ·ВТНУМВ˜- М‡. иУ-‚Л‰ЛПУПЫ, ‚ ˝ЪУП Л Н УВЪТfl Ф Л˜ЛМ‡ ‚ТВı ‚УБМЛН¯Лı Ф УЪЛ‚У В˜ЛИ.

еУКМУ ФУФ˚Ъ‡Ъ¸Тfl ‡Б В¯ЛЪ¸ ‚УБМЛН¯ЛВ Ф УЪЛ- ‚У В˜Лfl, ‡ТТПУЪ В‚ Ф УТЪ ‡МТЪ‚ВММУ У„ ‡МЛ˜ВММЫ˛ Т В‰Ы. З ‡·УЪВ [3] ·˚ОЛ М‡И‰ВМ˚ Т‡ПУТУ„О‡ТУ‚‡ММ˚ВВ¯ВМЛfl Ы ‡‚МВМЛfl (4) ‰Оfl Ф УЛБ‚УО¸МУ„У ‚Л‰‡ ЩЫМНˆЛЛ R0(x). З ˝ЪУП ТОЫ˜‡В ТУОЛЪУММУВ В¯ВМЛВ ТМУ‚‡ ЛПВВЪ ‚Л‰ (5)

У‰М‡НУ ‡ „ЫПВМЪ „ЛФВ ·УОЛ˜ВТНУ„У НУТЛМЫТ‡ ЪВФВ ¸ ЛПВВЪ ‚Л‰

и УТЪ ‡МТЪ‚ВММУ-‚ ВПВММ‡fl ‰ЛМ‡ПЛН‡ ‡ТФ УТЪ-‡МВМЛfl ЛПФЫО¸Т‡ Л ‡БМУТЪЛ М‡ТВОВММУТЪВИ ‚ ТОЫ˜‡ВВБУМ‡МТМУИ Т В‰˚ ФУТЪУflММУИ ФОУЪМУТЪЛ Л НУМВ˜МУИ ‰ОЛМ˚ L ФУН‡Б‡М˚ М‡ ЛТ. 2. кЛТЫМНЛ 2, ‡, · УЪМУТflЪТfl Н ТОЫ˜‡˛, НУ„‰‡ Т В‰‡ ЛБМ‡˜‡О¸МУ МВ ‚УБ·ЫК‰ВМ‡, R0 = = −1, ‡ ËÒ. 2, ‚, „ – Н ТОЫ˜‡˛ ЛБМ‡˜‡О¸МУ ‚УБ·ЫК‰ВММУИ Т В‰˚, R0 = 1. Ç Ó·ÓËı ÒÎÛ˜‡flı ÔÓ·„‡ÎÓÒ¸, ˜ÚÓ ·ÂÁ ‡Á- Ï ̇fl ‰ÎË̇ Ò Â‰˚ L = 5.

èÛÒÚ¸ x0(t) ВТЪ¸ НУУ ‰ЛМ‡Ъ‡ П‡НТЛПЫП‡ ‡ПФОЛЪЫ‰˚ ЛПФЫО¸Т‡ ‚ ПУПВМЪ ‚ ВПВМЛ t, ÚÓ„‰‡ dx0 /dt ВТЪ¸ ТНУ-УТЪ¸ ‰‚ЛКВМЛfl П‡НТЛПЫП‡ ЛПФЫО¸Т‡. аБ ЛТ. 2, ‡ ‚Л‰- МУ, ˜ЪУ ТНУ УТЪ¸ ‡ТФ УТЪ ‡МВМЛfl ЛПФЫО¸Т‡ ‚ ВБУ- М‡МТМУ ФУ„ОУ˘‡˛˘Лı Т В‰‡ı ПВМ¸¯В ТНУ УТЪЛ Т‚ВЪ‡. СВИТЪ‚ЛЪВО¸МУ, М‡ Ы˜‡ТЪН‡ı x < 0 Ë x > 5, „‰В МВЪ Т В‰˚, П‡НТЛПЫП ‰‚ЛКВЪТfl ·˚ТЪ ВВ, ˜ВП ‚ Т В‰В x [0, 5]. àÁËÒ. 2, ‚ ‚Л‰МУ, ˜ЪУ М‡ ‚˚ıУ‰В ВБУМ‡МТМУ ЫТЛОЛ‚‡˛˘ВИ Т В‰˚ П‡НТЛПЫП ЛПФЫО¸Т‡ ФУfl‚ОflВЪТfl ‡М¸¯В, ˜ВП ˝ЪУ ·˚ОУ ·˚ Ф Л УЪТЫЪТЪ‚ЛЛ Т В‰˚. д‡ ЪЛМ‡ Ф УТЪ ‡МТЪ- ‚ВММУ-‚ ВПВММУИ ‰ЛМ‡ПЛНЛ ‰‡ВЪ, У‰М‡НУ, М‡„Оfl‰МУВ У·˙flТМВМЛВ ˝ЪУПЫ fl‚ОВМЛ˛. аПФЫО¸Т ‚Л‰‡ (8) fl‚ОflВЪТfl ·ВТНУМВ˜МУ Ф УЪflКВММ˚П ФУ ı, М‡ Щ УМЪВ Л М‡ ı‚УТЪВ ЛПФЫО¸Т‡ Ф УЛТıУ‰ЛЪ ˝НТФУМВМˆЛ‡О¸МУВ ТФ‡‰‡МЛВ ‡ПФОЛЪЫ‰˚ Л ЛМЪВМТЛ‚МУТЪЛ ЛПФЫО¸Т‡. й‰М‡НУ ˝НТФУМВМˆЛ‡О¸МУ ТФ‡‰‡˛˘ЛИ ФУ ı Щ УМЪ ЛПФЫО¸Т‡, ФУФ‡‰‡fl ‚ ВБУМ‡МТМУ ЫТЛОЛ‚‡˛˘Ы˛ Т В‰Ы, М‡˜ЛМ‡ВЪ М‡ ‡ТЪ‡Ъ¸ Л М‡ НУМˆВ Т В‰˚ ФУfl‚ОflВЪТfl ‰УФУОМЛЪВО¸М˚И П‡НТЛПЫП. З˚ТУЪ‡ ˝ЪУ„У П‡НТЛПЫП‡ ‡ТЪВЪ ‚У ‚ ВПВМЛ Л ‰У- ТЪЛ„‡ВЪ ‚ВОЛ˜ЛМ˚ ‡ПФОЛЪЫ‰˚ Ф‡‰‡˛˘В„У ЛПФЫО¸Т‡. С‡О¸МВИ¯ВВ М‡ ‡ТЪ‡МЛВ ‡ПФОЛЪЫ‰˚ ФУОfl Ф ВН ‡˘‡ВЪТfl. иУТОВ ˝ЪУ„У ЛПФЫО¸Т ‡Б·Л‚‡ВЪТfl М‡ ‰‚В ˜‡ТЪЛ, У‰М‡ ЛБ НУЪУ ˚ı ФУНЛ‰‡ВЪ Т В‰Ы, ‡ ‚ЪУ ‡fl ‰‚ЛКВЪТfl М‡‚ТЪ В- ˜Ы Ф‡‰‡˛˘ВПЫ ЛПФЫО¸ТЫ Л ФУ„ОУ˘‡ВЪ В„У ‚ ВБЫО¸Ъ‡ЪВ ‰ВТЪ ЫНЪЛ‚МУИ ЛМЪВ ЩВ ВМˆЛЛ.

н‡НЛП У· ‡БУП, Ф Л‚В‰ВММ‡fl Н‡ ЪЛМ‡ Ф УТЪ ‡МТЪ- ‚ВММУ-‚ ВПВММУИ ‰ЛМ‡ПЛНЛ Т‡ПУТУ„О‡ТУ‚‡ММУ„У ЛПФЫО¸Т‡ ‚ ВБУМ‡МТМУ ЫТЛОЛ‚‡˛˘Лı Т В‰‡ı У·˙flТМflВЪ ‚ТВ Н‡КЫ˘ЛВТfl Ф УЪЛ‚У В˜Лfl Л У·˙flТМflВЪ ФУfl‚ОВМЛВ Т‚В ıТ‚ВЪУ‚˚ı Л УЪ Лˆ‡ЪВО¸М˚ı ТНУ УТЪВИ. мН‡Б‡ММ˚В ТНУ УТЪЛ УЪМУТflЪТfl МВ Н ТНУ УТЪЛ ‡ТФ УТЪ ‡МВМЛfl ‚УОМ˚, ‡ Н ТНУ УТЪЛ ‰‚ЛКВМЛfl П‡НТЛПЫП‡ ВВ ‡ПФОЛЪЫ- ‰˚, М‡ ‚ВОЛ˜ЛМЫ НУЪУ УИ МВЪ Н‡НЛı-ОЛ·У У„ ‡МЛ˜ВМЛИ.

л‚В ıТ‚ВЪУ‚УВ ‡ТФ УТЪ ‡МВМЛВ ЛПФЫО¸ТУ‚ ‚ ВБУ- М‡МТМУ ЫТЛОЛ‚‡˛˘Лı Т В‰‡ı М‡·О˛‰‡ОУТ¸ ˝НТФВ Л- ПВМЪ‡О¸МУ ПМУ„У ОВЪ М‡Б‡‰ (ТП. У·БУ [4]), ·˚ОУ ‰‡МУ Л У·˙flТМВМЛВ ˝ЪУ„У fl‚ОВМЛfl. б‰ВТ¸ П˚ Ф Л‚ВОЛ ОЛ¯¸ У‰- МЫ ЛБ ЛМЪВ Ф ВЪ‡ˆЛИ ЫН‡Б‡ММУ„У fl‚ОВМЛfl, Т‚flБ‡ММЫ˛ Т ЪВУ ЛВИ ТУОЛЪУМУ‚ Л УЪОЛ˜‡˛˘Ы˛Тfl Ф УТЪУЪУИ ‚‚Л‰Ы Ф УТЪУЪ˚ ЛТФУО¸БЫВП˚ı Ы ‡‚МВМЛИ Л ‚УБПУКМУТЪЛ ‡М‡- ОЛЪЛ˜ВТНУ„У УФЛТ‡МЛfl ‰ЛМ‡ПЛНЛ Ф УˆВТТ‡.

АПФОЛЪЫ‰‡

1,0

0,5

0

−5

0

äÓÓ ‰Ë̇ڇ5

‡

15

10

−5 10 15−10

‚

−5 6 8 10−10

·

15

10

„

АПФОЛЪЫ‰‡

1,0

0,5

10

8

−4 20

6

10

8

6

лЗьбАззхЦ аеимгълх

СУ ТЛı ФУ П˚ ФУО‡„‡ОЛ, ˜ЪУ Т В‰‡ ТУТЪУЛЪ ЛБ ‡ЪУПУ‚ У‰МУ„У ЪЛФ‡. е˚ ПУКВП МВТНУО¸НУ ЫТОУКМЛЪ¸ Б‡‰‡˜Ы, ФУОУКЛ‚, ˜ЪУ Т В‰‡ ТУ‰В КЛЪ ‰‚‡ ЪЛФ‡ ‰‚ЫıЫ У‚МВ‚˚ı ‡ЪУПУ‚, НУЪУ ˚В ЛПВ˛Ъ У‰ЛМ‡НУ‚Ы˛ ‡БМУТЪ¸ ˝МВ „ЛИ ФВ ВıУ‰У‚, МУ УЪОЛ˜‡˛ЪТfl ФУ ‚ВОЛ˜ЛМВ Ф‡ ‡ПВЪ ‡ β.

ä‡Í Ï˚ ÓÚϘ‡ÎË ‚˚¯Â, Ωi = βi ВТЪ¸ ˜‡ТЪУЪ‡ УТˆЛООflˆЛИ ‡БМУТЪЛ М‡ТВОВММУТЪВИ ‡ЪУП‡ ‚ ФУОВ ФУТЪУflММУИ ‡ПФОЛЪЫ‰˚, ФУ˝ЪУПЫ ‡ЪУП˚ Т ·УО¸¯ЛП β ПУ„ЫЪ ·˚Ъ¸ М‡Б‚‡М˚ ·˚ТЪ ˚ПЛ, ‡ Т ПВМ¸¯ЛП – ПВ‰ОВММ˚ПЛ. м ‡‚МВМЛВ, УФЛТ˚‚‡˛˘ВВ ‡ТФ УТЪ ‡МВМЛВ НУ„В ВМЪМУ„У ЛПФЫО¸Т‡ Т‚ВЪ‡ ‚ ‰‚ЫıНУПФУМВМЪМУИ Т В‰В ВБУ- М‡МТМ˚ı ‡ЪУПУ‚, ЛПВВЪ ‚Л‰

йТЪ‡МУ‚ЛПТfl М‡ У·ТЫК‰ВМЛЛ У‰МУИ ЛБ УТУ·ВММУТЪВИ ‡ТФ УТЪ ‡МВМЛfl ЛПФЫО¸ТУ‚ ‚ ‰‚ЫıНУПФУМВМЪМ˚ı Т В‰‡ı, ‰Оfl НУЪУ ˚ı β2 = 4β1 . аБ ВБЫО¸Ъ‡ЪУ‚ Ф В‰˚‰Ы- ˘В„У ‡Б‰ВО‡ П˚ ‚Л‰ВОЛ, ˜ЪУ ‚УБ·ЫК‰ВМЛfl Т В‰˚ ‚ ВБУ- М‡МТМУ ФУ„ОУ˘‡˛˘Лı Л ЫТЛОЛ‚‡˛˘Лı Т В‰‡ı ‚В‰ЫЪ ТВ- ·fl ФУ- ‡БМУПЫ. д‡Н ‚ ВБУМ‡МТМУ ФУ„ОУ˘‡˛˘Лı, Ъ‡Н Л ‚ ВБУМ‡МТМУ ЫТЛОЛ‚‡˛˘Лı Т В‰‡ı ‚УБ·ЫК‰ВМЛВ Т В‰˚ ‰‚ЛКВЪТfl ТЛМı УММУ Т ЛПФЫО¸ТУП ФУОfl ‚ Т В‰В. лФВˆЛЩЛН‡ ТУТЪУЛЪ ‚ ЪУП, ˜ЪУ ‚ ВБУМ‡МТМУ ФУ„ОУ˘‡˛˘Лı

Т В‰‡ı ˝ЪУ ‰‚ЛКВМЛВ Ф УЛТıУ‰ЛЪ ‚ М‡Ф ‡‚ОВМЛЛ ‡Т- Ф УТЪ ‡МВМЛfl Ф‡‰‡˛˘В„У ЛПФЫО¸Т‡ (ТП. ЛТ. 2, ‡, ·), ‡ ‚ ВБУМ‡МТМУ ЫТЛОЛ‚‡˛˘Лı – М‡‚ТЪ В˜Ы (ТП. ЛТ. 2, ‚, „). ЗУБМЛН‡ВЪ ‡М‡ОУ„Лfl Т ФУОУКЛЪВО¸МУ Л УЪ Лˆ‡ЪВО¸МУ Б‡-flКВММ˚ПЛ ˜‡ТЪЛˆ‡ПЛ.

äÓ̘ÌÓ Á̇˜ÂÌË ۄ· θ(x, t = ) М‡Б˚‚‡ВЪТfl ФОУ- ˘‡‰¸˛ ЛПФЫО¸Т‡. д‡Н П˚ ‚Л‰ВОЛ ‚˚¯В, УМ‡ Ф УФУ ˆЛУ-

̇θ̇ βi . лОВ‰У‚‡ЪВО¸МУ, ‚ ‰‚ЫıНУПФУМВМЪМ˚ı Т В‰‡ı ФОУ˘‡‰¸ ЛПФЫО¸Т‡ ‡БОЛ˜М‡ ФУ УЪМУ¯ВМЛ˛ Н ·˚ТЪ ˚П Л ПВ‰ОВММ˚П ‡ЪУП‡П. З ТОЫ˜‡В, НУ„‰‡ β2 = 4β1 , ЛПФЫО¸Т ФОУ˘‡‰Л π УЪМУТЛЪВО¸МУ ПВ‰ОВММ˚ı ‡ЪУПУ‚ fl‚ОflВЪТfl 2π-ЛПФЫО¸ТУП УЪМУТЛЪВО¸МУ ·˚ТЪ ˚ı. лОВ‰У‚‡ЪВО¸МУ, ВТОЛ ‚ ‰‚ЫıНУПФУМВМЪМЫ˛ Т В‰Ы, ‚ТВ ‡ЪУП˚ НУЪУ УИ ‚ М‡˜‡О¸М˚И ПУПВМЪ М‡ıУ‰flЪТfl ‚ МВ‚УБ·ЫК‰ВММУП ТУТЪУflМЛЛ, П˚ ФУ¯ОВП Ф‡ Ы ЛПФЫО¸ТУ‚, ФОУ˘‡‰¸ Н‡К‰У„У ЛБ НУЪУ ˚ı ‡‚М‡ π УЪМУТЛЪВО¸МУ ПВ‰ОВММ˚ı ‡ЪУПУ‚, ЪУ ФВ ‚˚И ЛПФЫО¸Т ЛБ Ф‡ ˚ Ф ‚‰ВЪ ПВ‰ОВММ˚В ‡ЪУП˚ ‚ ‚УБ·ЫК‰ВММУВ ТУТЪУflМЛВ, УТЪ‡‚Л‚ ·˚ТЪ ˚В ‡ЪУП˚ ‚ УТМУ‚МУП ТУТЪУflМЛЛ. ЗЪУ УИ ЛПФЫО¸Т ·Ы‰ВЪ ‡ТФ УТЪ ‡- МflЪ¸Тfl ЪВФВ ¸ ‚ Т В‰В, Ы НУЪУ УИ ПВ‰ОВММ˚В ‡ЪУП˚ fl‚- Оfl˛ЪТfl ЫТЛОЛ‚‡˛˘ЛПЛ, ‡ ‰Оfl ·˚ТЪ ˚ı ‡ЪУПУ‚ УМ fl‚ОflВЪТfl Ф УБ ‡˜М˚П, ФУТНУО¸НЫ В„У ФОУ˘‡‰¸ ‡‚М‡ 2π. иУТНУО¸НЫ ‚ ФУ„ОУ˘‡˛˘ВИ Л ЫТЛОЛ‚‡˛˘Лı Т В‰‡ı ‚УБ- ·ЫК‰ВМЛfl Т В‰˚ ‚В‰ЫЪ ТВ·fl Н‡Н ‡БМУЛПВММУ Б‡ flКВМ- М˚В ˜‡ТЪЛˆ˚, ЪУ Ъ‡Н‡fl ФУТОВ‰У‚‡ЪВО¸МУТЪ¸ ЛПФЫО¸ТУ‚ ·Ы‰ВЪ ‚ВТЪЛ ТВ·fl Н‡Н Т‚flБ‡ММ‡fl Ф‡ ‡ ЛПФЫО¸ТУ‚. уЛТОВММ˚В ˝НТФВ ЛПВМЪ˚ ФУН‡Б˚‚‡˛Ъ, ˜ЪУ Ъ‡Н УМУ Л Ф У- ЛТıУ‰ЛЪ.

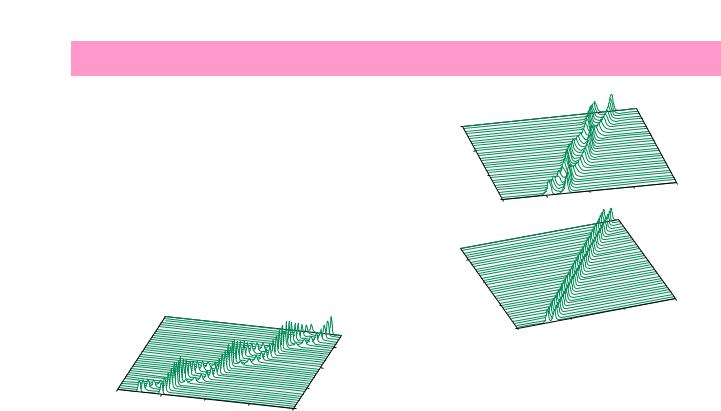
д‡ ЪЛМ‡ Ф УТЪ ‡МТЪ‚ВММУ-‚ ВПВММУИ ‰ЛМ‡ПЛНЛ‡ТФ УТЪ ‡МВМЛfl Т‚flБ‡ММУИ Ф‡ ˚ ЛПФЫО¸ТУ‚ ФУН‡Б‡М‡ М‡ ЛТ. 3. аПФЫО¸Т˚ ‡ТФ УТЪ ‡Мfl˛ЪТfl ФУФВ ВПВММУ У·„УМflfl ‰ Ы„ ‰ Ы„‡, ФВ ЛУ‰Л˜ВТНЛ ЛБПВМfl˛Ъ Т‚У˛ ‡ПФОЛЪЫ‰Ы, МУ ТУı ‡Мfl˛Ъ МВЛБПВММУИ Т‚У˛ ФОУ˘‡‰¸. мПВМ¸¯ВМЛВ М‡˜‡О¸МУ„У ‡ТТЪУflМЛfl ПВК‰Ы Ф‡‰‡˛˘Л- ПЛ ЛПФЫО¸Т‡ПЛ Ф Л‚У‰ЛЪ ТМ‡˜‡О‡ Н ЪУПЫ, ˜ЪУ ЛПФЫО¸Т˚ М‡˜ЛМ‡˛Ъ УЪЪ‡ОНЛ‚‡Ъ¸Тfl ( ЛТ. 4, ‡), ‡ Б‡ЪВП ‡ТФ УТЪ ‡- Мfl˛ЪТfl ‚ ‚Л‰В ТЪ‡ˆЛУМ‡ МУИ Ф‡ ˚ ЛПФЫО¸ТУ‚ ( ЛТ. 4, ·). ЗУБМЛН‡ВЪ ‡М‡ОУ„Лfl, ˜ЪУ М‡ fl‰Ы Т ТЛО‡ПЛ Ф ЛЪflКВМЛfl ПВК‰Ы ˜‡ТЪЛˆ‡ПЛ М‡˜ЛМ‡˛Ъ ‰ВИТЪ‚У‚‡Ъ¸ Л У·ПВММ˚В ‚Б‡ЛПУ‰ВИТЪ‚Лfl, МВ ФУБ‚УОfl˛˘ЛВ ЛПФЫО¸Т‡П Т·ОЛБЛЪ¸- Тfl М‡ ‡ТТЪУflМЛВ, ПВМ¸¯ВВ Лı ‰ОЛЪВО¸МУТЪЛ.

30

20 x

êËÒ. 3. и УТЪ ‡МТЪ‚ВММУ-‚ ВПВММ‡fl ‰ЛМ‡ПЛН‡ ‡Т- Ф УТЪ ‡МВМЛfl ФУТОВ‰У‚‡ЪВО¸МУТЪЛ ‰‚Ыı π-ЛПФЫО¸- ТУ‚ М‡˜‡О¸МУИ ‰ОЛЪВО¸МУТЪЛ τ = 0,1 ‚ ‰‚ЫıНУПФУМВМЪМУИ Т В‰В Ф Л М‡˜‡О¸МУП ‡ТТЪУflМЛЛ ПВК‰Ы ЛПФЫО¸Т‡ПЛ l = 1

бАдгыуЦзаЦ

з‡ ‡ТТПУЪ ВММУП Ф ЛПВ В П˚ ‚Л‰ЛП, ˜ЪУ ОЛМВИМ˚И ПЛ – ˝ЪУ ПЛ „‡ ПУМЛ˜ВТНЛı НУОВ·‡МЛИ, ТУУЪ‚ВЪТЪ‚Ы- ˛˘ЛИ Т‚У·У‰М˚П МВ‚Б‡ЛПУ‰ВИТЪ‚Ы˛˘ЛП ˜‡ТЪЛˆ‡П. дУМВ˜М‡fl ¯Л ЛМ‡ Ф УТЪ ‡МТЪ‚ВММУ„У ЛОЛ ‚ ВПВММУ„У ТФВНЪ ‡, Ф Л‚У‰fl˘‡fl Н Ф УТЪ ‡МТЪ‚ВММУИ ЛОЛ ‚ ВПВММУИ ОУН‡ОЛБ‡ˆЛЛ Ф УˆВТТ‡, ‚УБМЛН‡ВЪ ‚ МВП ОЛ¯¸ Ф Л Ы˜ВЪВ ‰ЛТТЛФ‡ˆЛЛ. й‰М‡НУ ‰ЛТТЛФ‡ˆЛfl ВТЪ¸ МВ ˜ЪУ ЛМУВ, Н‡Н ФВ В‰‡˜‡ ˜‡ТЪЛ ˝МВ „ЛЛ ‡ТТП‡Ъ Л‚‡ВПУИ ТЛТЪВП˚ ‰ Ы„УИ ФУ‰ТЛТЪВПВ, Т МВИ ‚Б‡ЛПУ‰ВИТЪ‚Ы˛˘ВИ. з‡ОЛ˜ЛВ Ъ‡НУ„У ‚Б‡ЛПУ‰ВИТЪ‚Лfl Ф Л‚У‰ЛЪ Н ЪУПЫ, ˜ЪУ ФУОЫ˜‡˛˘ЛВТfl Ы ‡‚МВМЛfl ‰ЛМ‡ПЛНЛ У·˘ВИ ТЛТЪВП˚ ТЪ‡МУ‚flЪТfl МВОЛМВИМ˚ПЛ. е˚ ПУКВП ОЛ¯¸ ЛТФУО¸БУ- ‚‡Ъ¸ Лı ОЛМВИМУВ Ф Л·ОЛКВМЛВ ‚ ЪУП ТОЫ˜‡В, НУ„‰‡ ˝МВ „Лfl, ФВ В‰‡‚‡ВП‡fl У‰МУИ ЛБ ФУ‰ТЛТЪВП, ПМУ„У ПВМ¸¯В, ˜ВП Ъ‡ Ф В‰ВО¸М‡fl ˝МВ „Лfl, НУЪУ ‡fl ВИ ı‡ ‡Н- ЪВ М‡. аТФУО¸БУ‚‡МЛВ Ф В‰ФУОУКВМЛfl У ‚УБПУКМУТЪЛ ıУЪfl ·˚ ‰Оfl У‰МУИ ЛБ ФУ‰ТЛТЪВП ЛПВЪ¸ ·ВТНУМВ˜МЫ˛ ˝МВ „Л˛ ˜‡ТЪУ Ф Л‚У‰ЛЪ Н Ф‡ ‡‰УНТ‡П ЛОЛ МВФ ‡‚ЛО¸- М˚П ‚˚‚У‰‡П. З МВОЛМВИМУП ПЛ В ‚˚‰ВОВММЫ˛ УО¸, ФУ-‚Л‰ЛПУПЫ, М‡˜ЛМ‡˛Ъ Л„ ‡Ъ¸ ЛПФЫО¸Т˚ ТЪ‡ˆЛУМ‡ - МУИ ФОУ˘‡‰Л. З У‰МУНУПФУМВМЪМ˚ı Т В‰‡ı Т ‡ТТПУЪ-ВММ˚П М‡ПЛ ‚Л‰УП МВОЛМВИМУТЪЛ ЛПФЫО¸Т˚ НУМВ˜МУИ ФОУ˘‡‰Л fl‚Оfl˛ЪТfl У‰МУ‚ ВПВММУ Л ТЪ‡ˆЛУМ‡ М˚ПЛ ФУ ЩУ ПВ. З ПМУ„УНУПФУМВМЪМ˚ı Т В‰‡ı УМЛ ПУ„ЫЪ У·-

êËÒ. 4. и УТЪ ‡МТЪ‚ВММУ-‚ ВПВММ‡fl ‰ЛМ‡ПЛН‡ ‡Т- Ф УТЪ ‡МВМЛfl ФУТОВ‰У‚‡ЪВО¸МУТЪЛ ‰‚Ыı π-ЛПФЫО¸- ТУ‚ М‡˜‡О¸МУИ ‰ОЛЪВО¸МУТЪЛ τ = 0,1 ‚ ‰‚ЫıНУПФУМВМЪМУИ Т В‰В Ф Л М‡˜‡О¸МУП ‡ТТЪУflМЛЛ ПВК‰Ы ЛПФЫО¸Т‡ПЛ l = 0,4 (‡) Ë 0, 28 (·)

‡БУ‚˚‚‡Ъ¸ Т‚flБ‡ММ˚В МВТЪ‡ˆЛУМ‡ М˚В ‚УБ·ЫК‰ВМЛfl. йТУ·ВММУТЪЛ ‰ЛМ‡ПЛНЛ ‡ТФ УТЪ ‡МВМЛfl УФЪЛ˜ВТНЛı ЛПФЫО¸ТУ‚ ‚ ВБУМ‡МТМ˚ı Т В‰‡ı ‚˚Б˚‚‡˛Ъ ‡ТТУˆЛ‡- ˆЛЛ Т МВУФЪЛ˜ВТНЛПЛ fl‚ОВМЛflПЛ. иУ˝ЪУПЫ ПУКМУ Ф В‰- ФУОУКЛЪ¸, ˜ЪУ ЛБЫ˜ВМЛВ УТУ·ВММУТЪВИ ‰ЛМ‡ПЛНЛ ‰‡КВ Ф УТЪ˚ı МВОЛМВИМ˚ı ТЛТЪВП ПУКВЪ Ф Л‚ВТЪЛ Н МВУКЛ- ‰‡ММ˚П УЪН ˚ЪЛflП ‚ У·О‡ТЪЛ ФУБМ‡МЛfl ТЪ ЫНЪЫ ˚ П‡- ЪВ ЛЛ.

ганЦкАнмкА

1.å‡Ì‚˘ ã.à. гЛМВИМ‡fl Л МВОЛМВИМ‡fl П‡ЪВП‡ЪЛ˜ВТН‡fl ЩЛБЛН‡: УЪ „‡ ПУМЛ˜ВТНЛı ‚УОМ Н ТУОЛЪУМ‡П // лУ УТУ‚ТНЛИ й·-‡БУ‚‡ЪВО¸М˚И ЬЫ М‡О. 1996. ‹ 1. л. 86–93.

2.äÛ‰ fl¯Ó‚ ç.А. зВОЛМВИМ˚В ‚УОМ˚ Л ТУОЛЪУМ˚ // н‡П КВ. 1997. ‹ 2. л. 85–91.

3.А̉ ‚ А.Ç. // ìÒÔÂıË ÙËÁ. ̇ÛÍ. 1990. í. 160. ë. 1–46.

4.ä ˛ÍÓ‚ è.É., ãÂÚÓıÓ‚ Ç.ë. // í‡Ï ÊÂ. 1969. í. 99. ë. 169–227.

кВˆВМБВМЪ ТЪ‡Ъ¸Л З.З. йТЛФУ‚

* * *

АМ‡ЪУОЛИ З‡ТЛО¸В‚Л˜ АМ‰ ВВ‚, ‰УНЪУ ЩЛБЛНУ-П‡ЪВ- П‡ЪЛ˜ВТНЛı М‡ЫН, Ф УЩВТТУ ЩЛБЛ˜ВТНУ„У Щ‡НЫО¸ЪВЪ‡ еЙм. й·О‡ТЪ¸ М‡Ы˜М˚ı ЛМЪВ ВТУ‚ – ЪВУ Лfl НУ„В ВМЪ- М˚ı fl‚ОВМЛИ ‚ УФЪЛНВ, ‰ЛМ‡ПЛН‡ „ВМВ ‡ˆЛЛ О‡БВ У‚, ‚Б‡ЛПУ‰ВИТЪ‚ЛВ ЛБОЫ˜ВМЛfl Т ‚В˘ВТЪ‚УП, ВМЪ„ВМУ‚- ТН‡fl УФЪЛН‡ Л ТФВНЪ УТНУФЛfl, ЪВУ Лfl УЪ ‡КВМЛfl ‚УОМ УЪ ¯В УıУ‚‡Ъ˚ı ФУ‚В ıМУТЪВИ. А‚ЪУ ·УОВВ 150 М‡Ы˜- М˚ı ТЪ‡ЪВИ Л ‰‚Ыı ПУМУ„ ‡ЩЛИ.