63. Сторонние силы. Электродвижущая сила и напряжение.

Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи: .

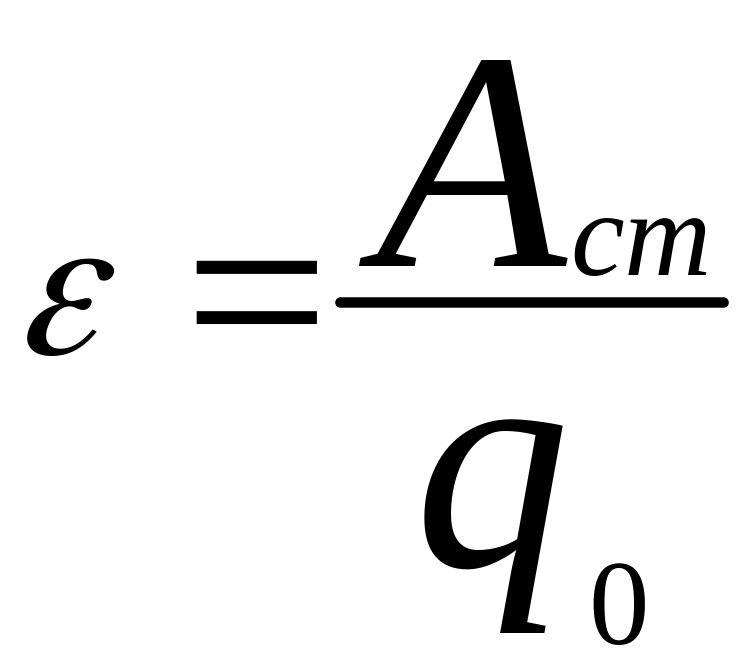Эта работа производится за счёт энергии, затрачиваемой в источнике тока, поэтому величину можно также назвать электродвижущей силой источника тока, включённого в цепь. ЭДС выражается в вольтах.

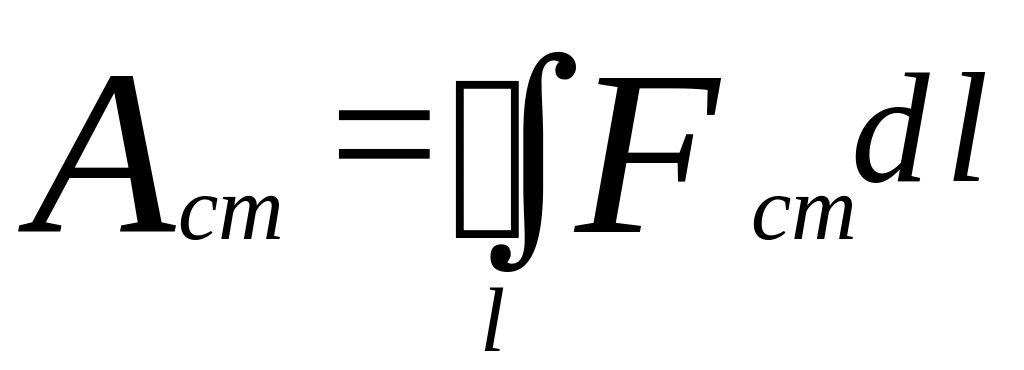
Сторонняя сила , действующая на заряд , может быть выражена как , где - напряжённость сторонних сил. Работа же сторонних сил по перемещению заряда на замкнутом участке цепи равна: т.к. , то 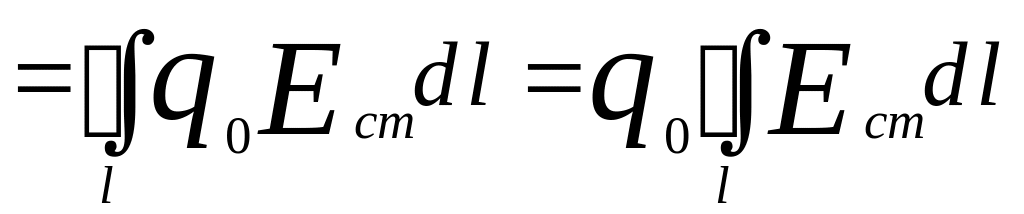. Тогда 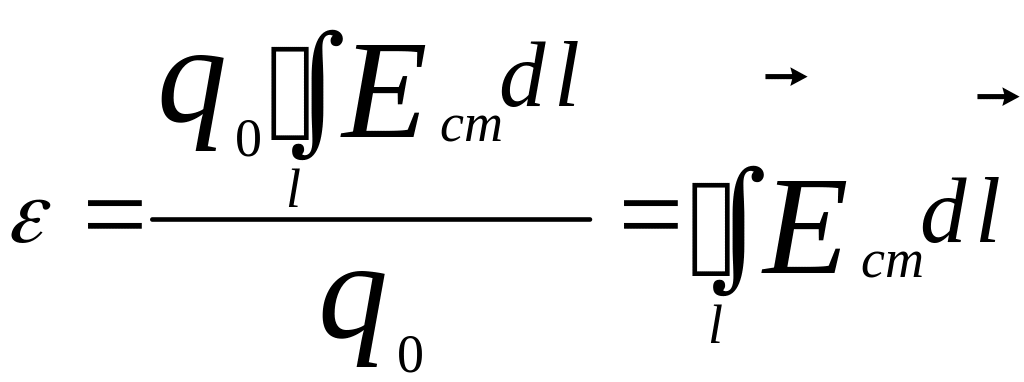, т.е. ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряжённости поля сторонних сил.

ЭДС, действующая на каком-нибудь участке 1 – 2, равна 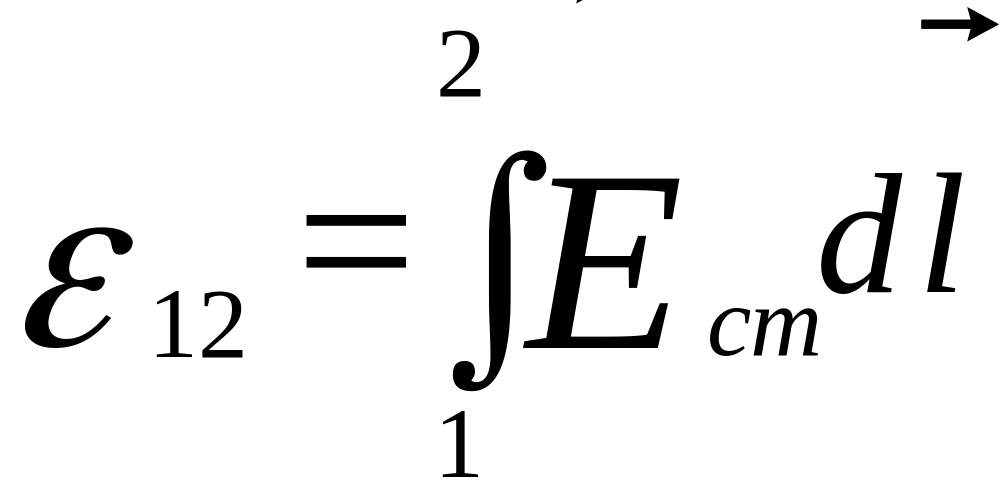. На заряд помимо сторонних сил действуют также силы электростатического поля . Т.о., результирующая сила, действующая в цепи на заряд , равна 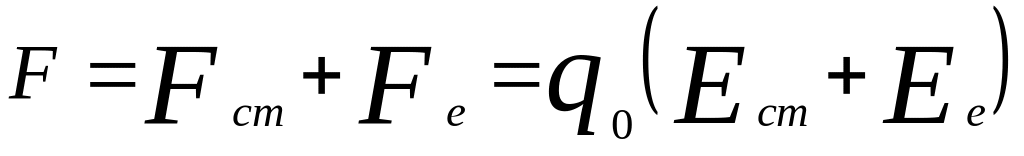. Работа, совершаемая результирующей силой над зарядом на участке 1 – 2, равна , .

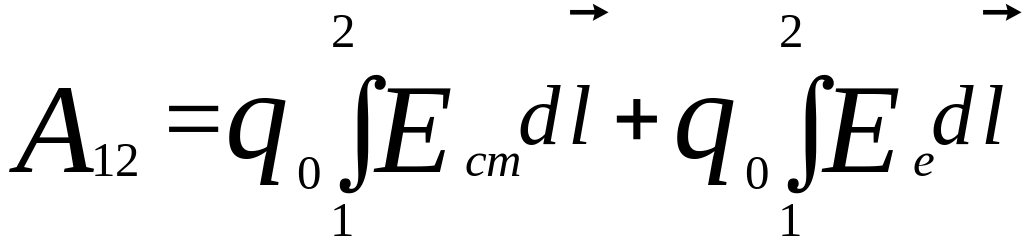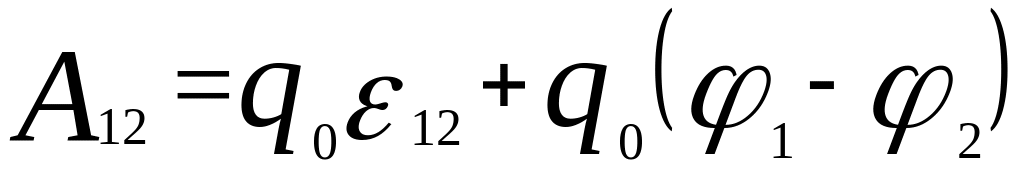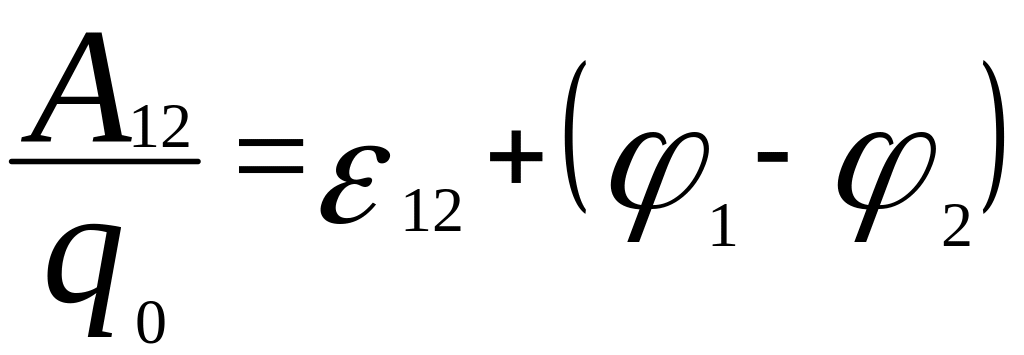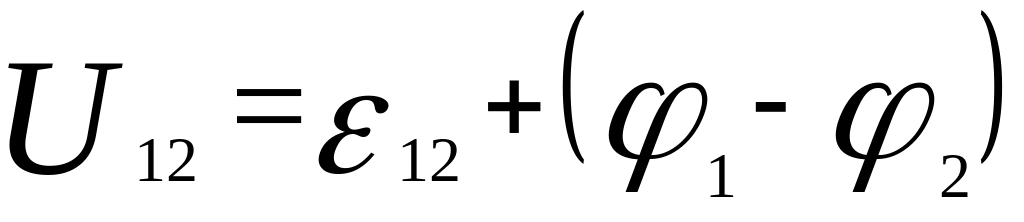, , . Напряжением U на участке 1 – 2 называется величина, определяемая работой, совершаемой суммарным полем электростатических и сторонних сил при перемещении единичного положительного заряда на данном участке цепи.

Понятие напряжения является обобщением понятия разности потенциалов в том случае, если на этом участке не действует ЭДС, т.е. сторонние силы отсутствуют.

64. Закон Ома для однородного участка цепи. Сопротивление проводников. Последовательное и параллельное соединение проводников.

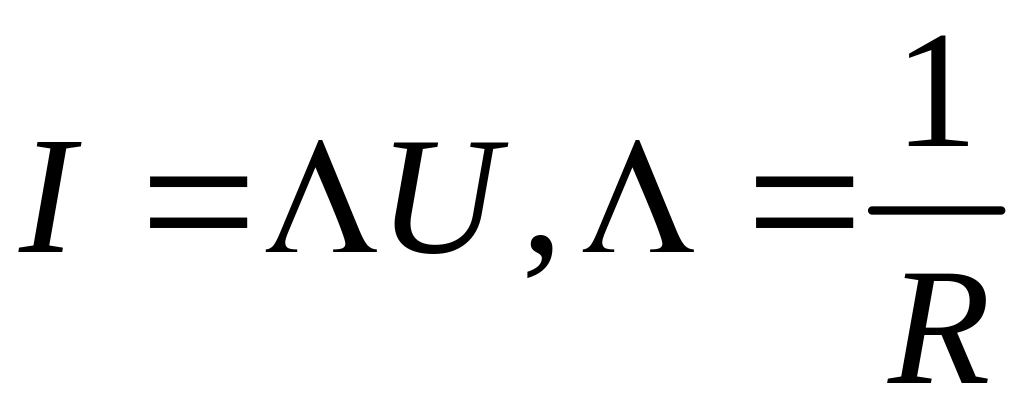. Тогда 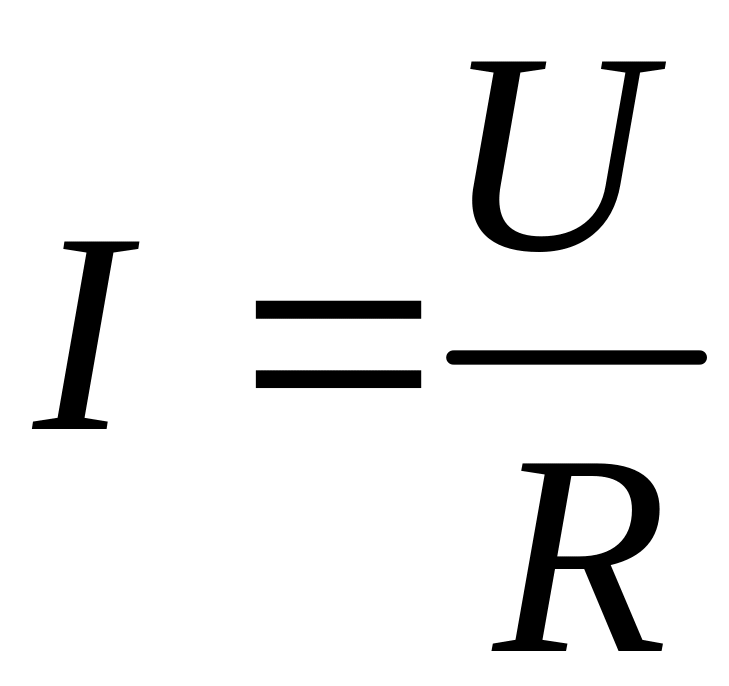, где U – напряжение на концах проводника, R – электрическое сопротивление проводника. Уравнение выражает закон Ома для участка цепи (не содержащего источника тока): сила тока на участке цепи, где отсутствуют сторонние силы, прямо пропорционально напряжению на концах этого участка и обратно пропорционально сопротивлению проводника. Единица измерения сопротивления – Ом: 1 Ом – сопротивление такого проводника, в котором при напряжении 1В течёт постоянный ток.

Величина 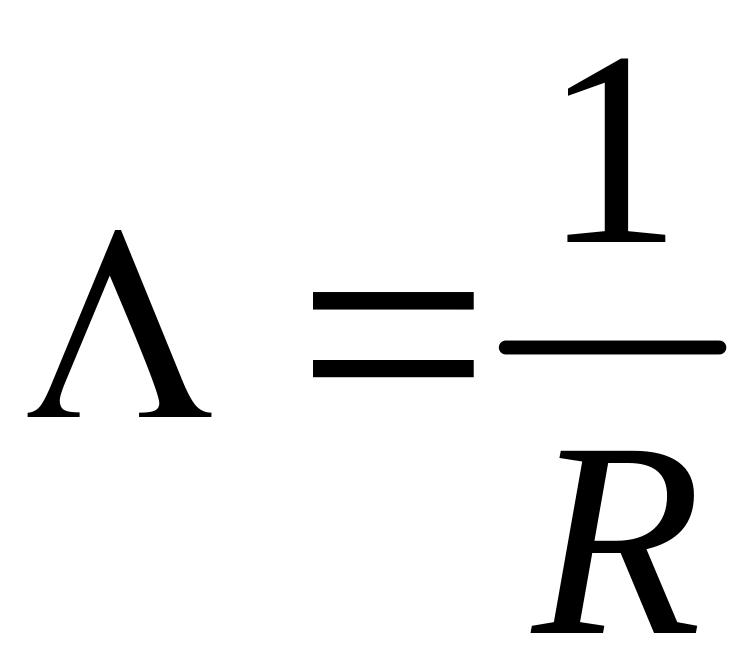называется электрической проводимостью проводника. Единица проводимости – сименс (См): 1См – проводимость участка электрической цепи сопротивлением 1 Ом.

Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S: 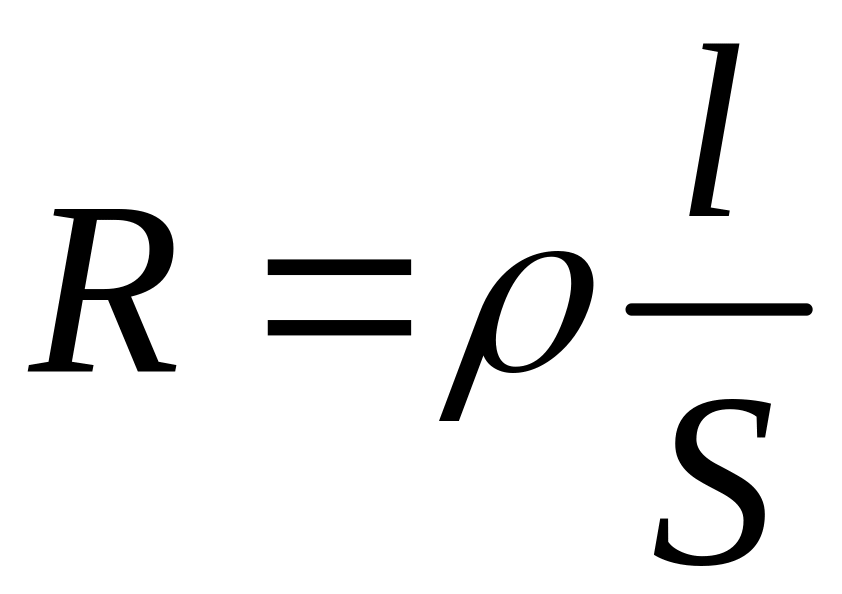, где - коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением. Единица удельного сопротивления – Ом-метр .

Последовательное соединение.

1. При последовательном соединении сила тока во всех участках цепи одинакова, т.е. .

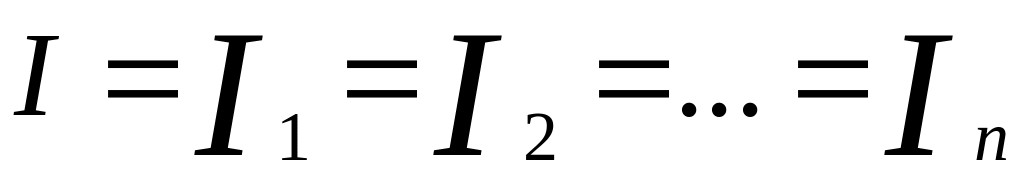2. При последовательном соединении напряжение на внешней цепи равно сумме напряжений на отдельных участках: , .

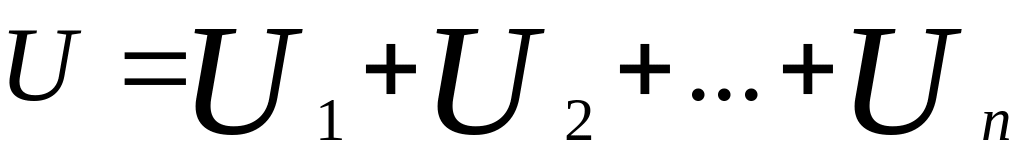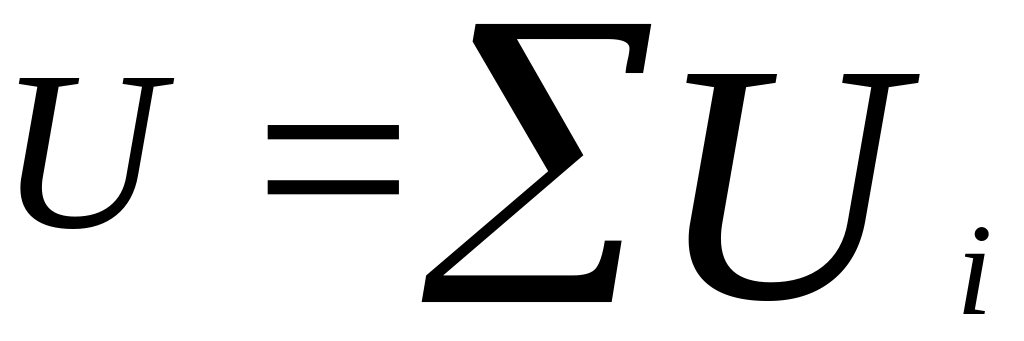3. Напряжения на отдельных участках при последовательном соединении прямо пропорциональны сопротивлениям участков: : :…= : :…

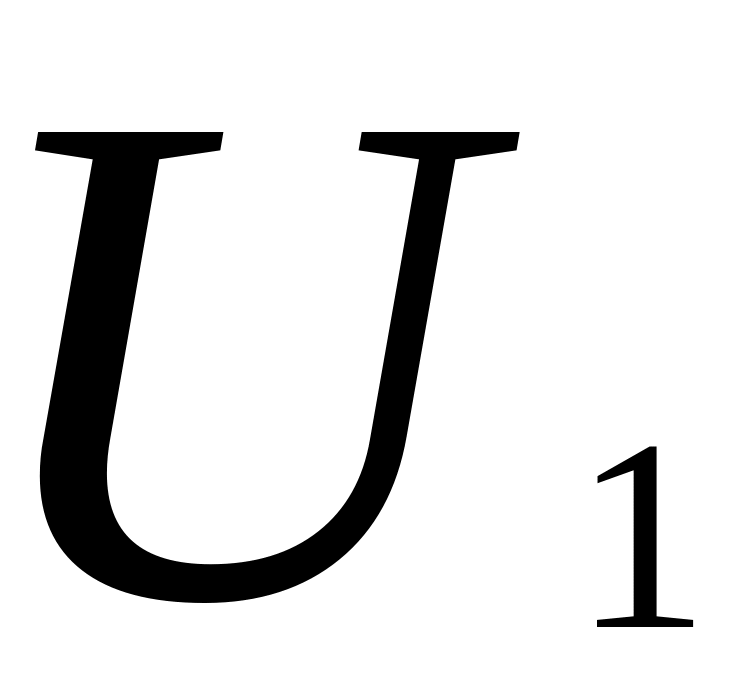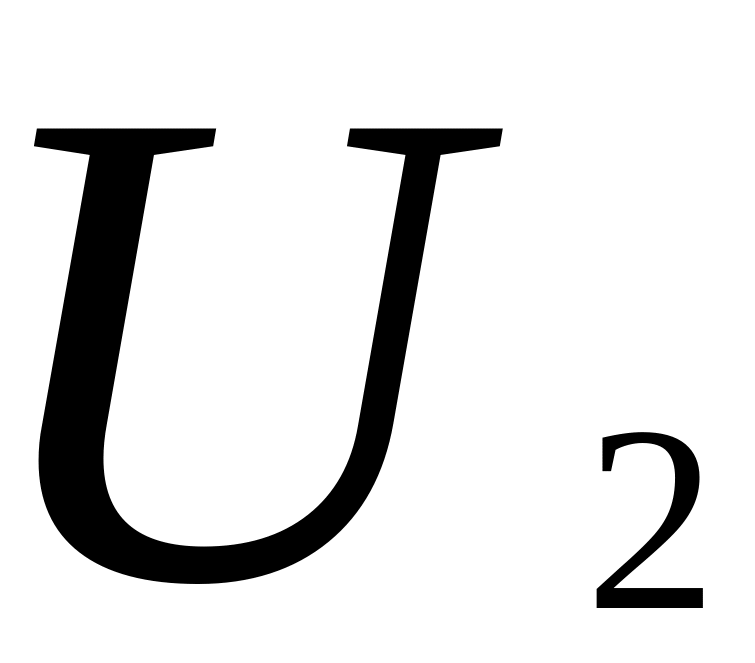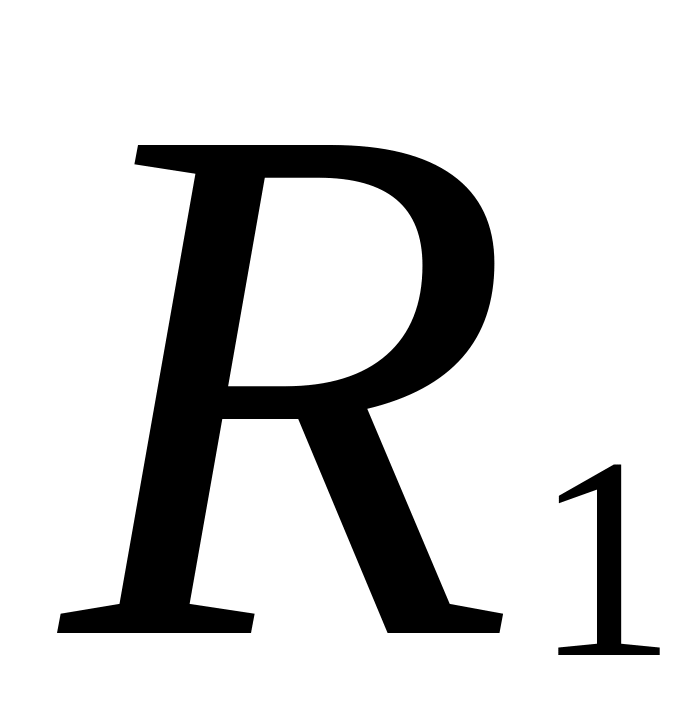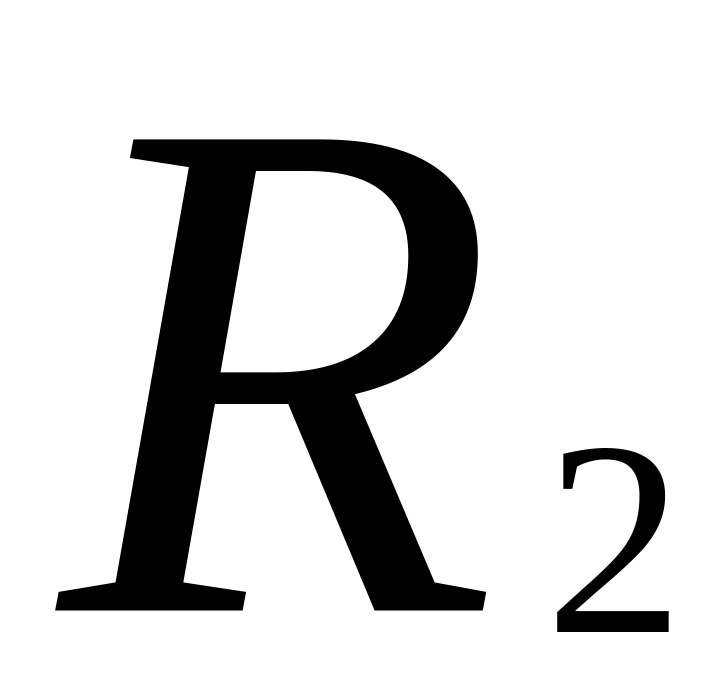4. При последовательном соединении сопротивлений эквивалентное сопротивление всей цепи равно сумме сопротивлений отдельных участков цепи: .

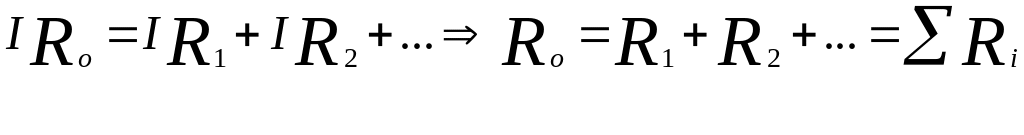Параллельное соединение.

1. При параллельном соединении проводников напряжение на отдельных ветвях и на всём разветвлении одинаково:

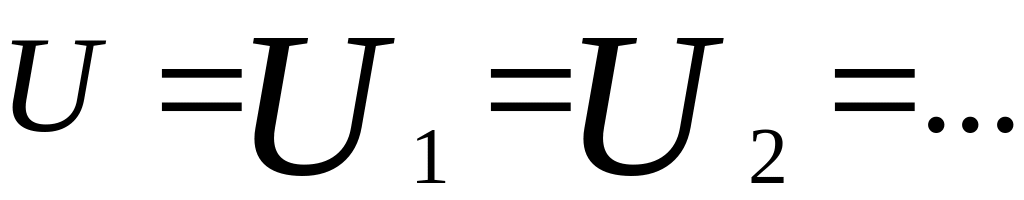
2. Ток до и после разветвления равен сумме токов в отдельных ветвях: .

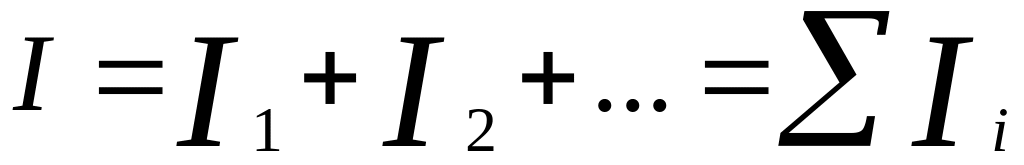3. Токи в отдельных ветвях разветвления обратно пропорциональны сопротивлениям этих ветвей: : :… = : :…

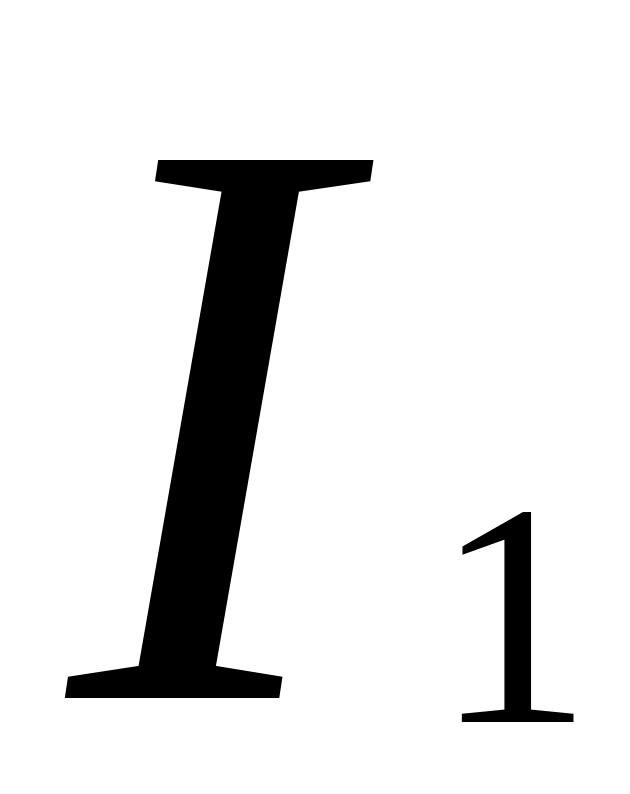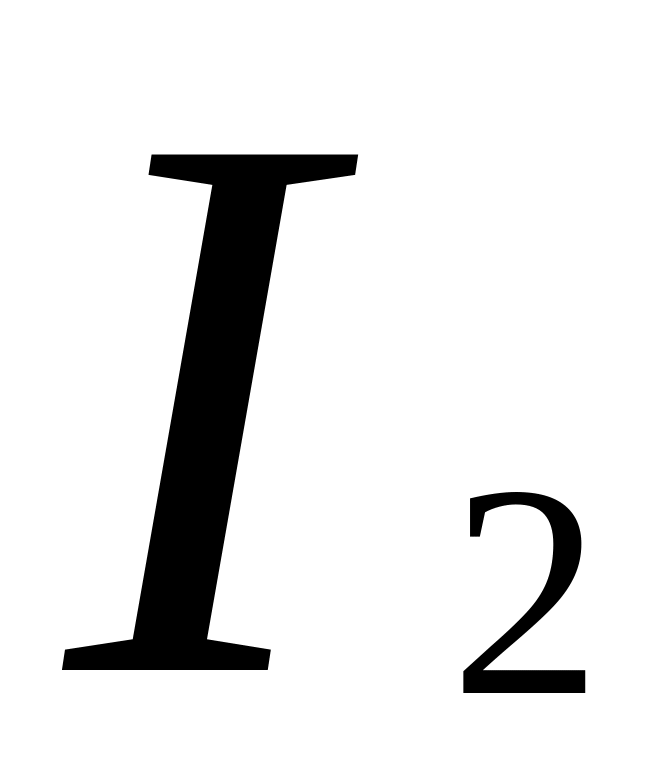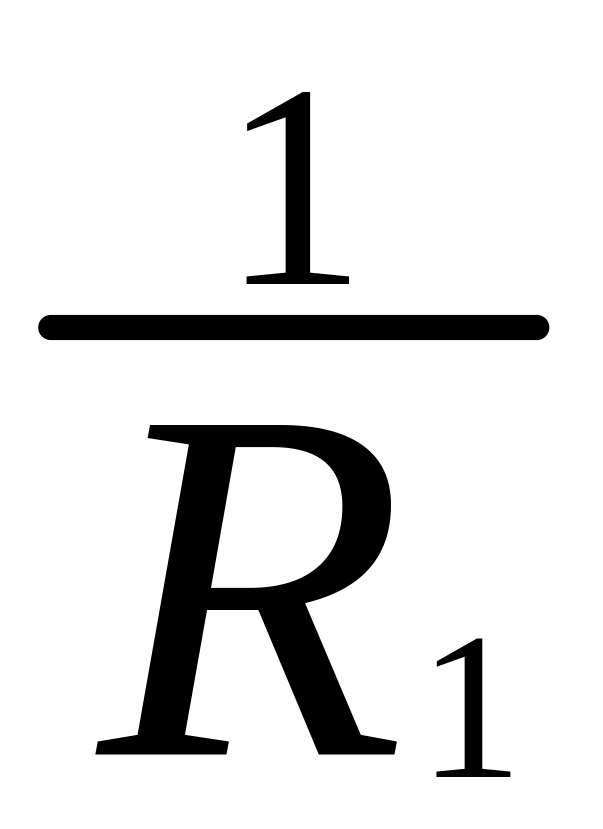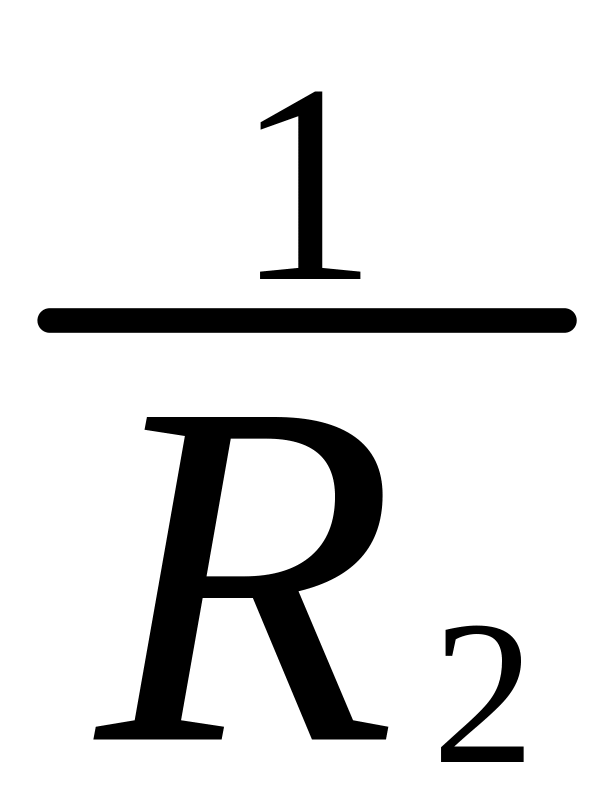4. Например, для 3-ёх проводников: , .

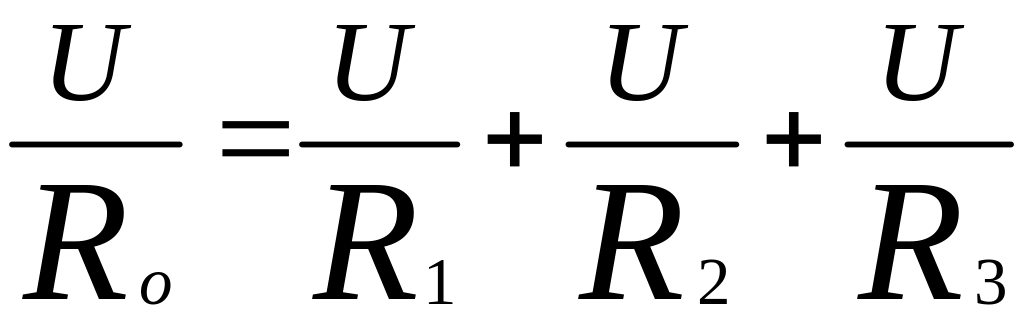65.Зависимость сопротивления от температуры.

*** , где - удельное электрическое сопротивление (коэффициент пропорциональности, характеризующий материал проводника, единица измерения - ).

Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит сопротивления, с температурой описывается линейным законом: , где и , - соответственно удельные сопротивления и сопротивления проводника при t, - температурный коэффициент сопротивления, для чистых металлов близкий к . Следовательно, температурная зависимость сопротивления может быть представлена в виде , где - термодинамическая температура.

Качественный ход температурной зависимости сопротивления металла представлен на рисунке.

В последствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах , называемых критическими, характерных для каждого вещества, т.е. металл становится абсолютным проводником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911 г. Г. Камерлинг-Оннесом для ртути. Практическое использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур.