2)Поле конденсатора

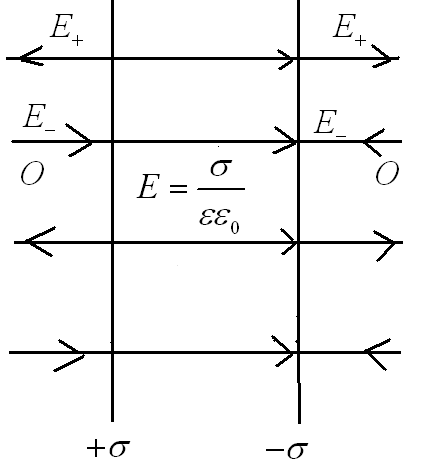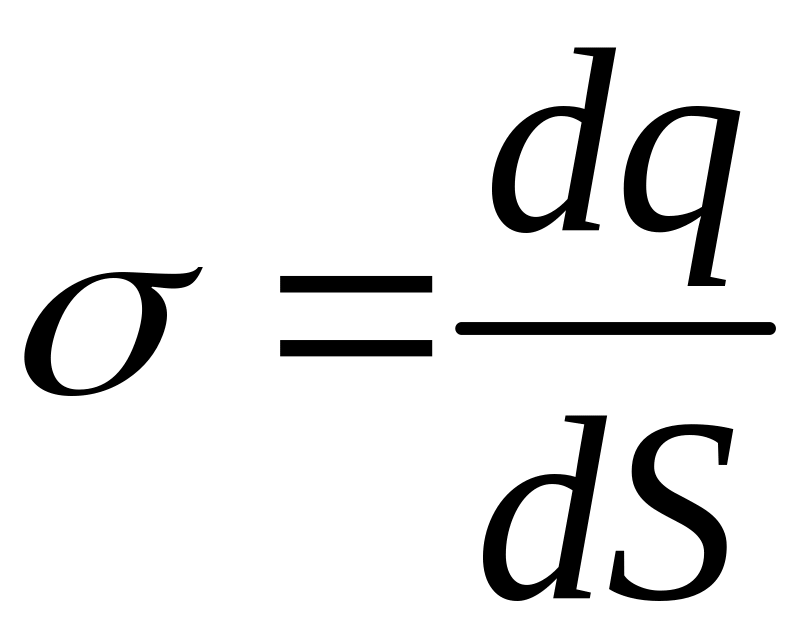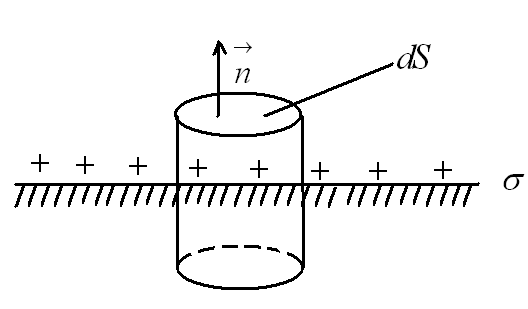
П усть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями и ( (*) - заряд, приходящийся на единицу поверхности). Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние – от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг к другу), поэтому напряженность поля . В области между плоскостями ( и определяются по формуле : (*** теорема Гаусса для вакуума***), поэтому результирующая напряженность 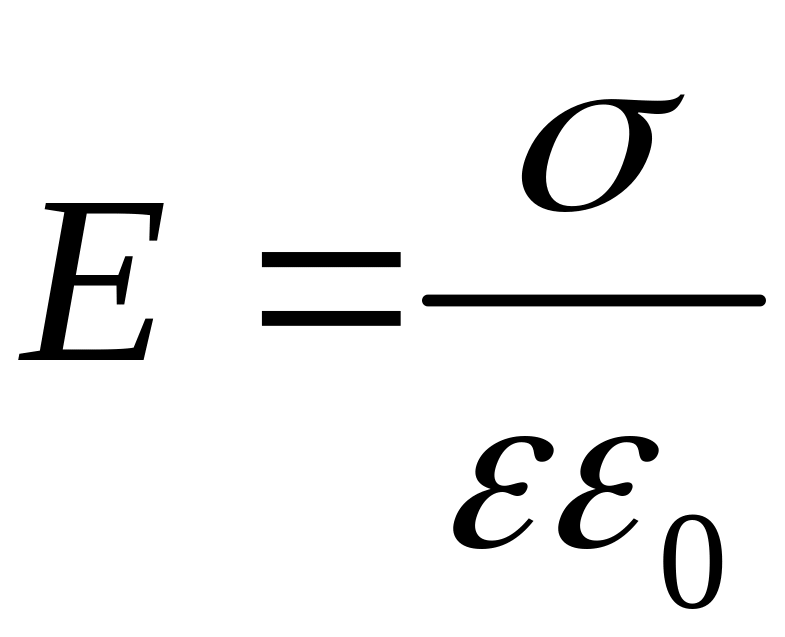, а .

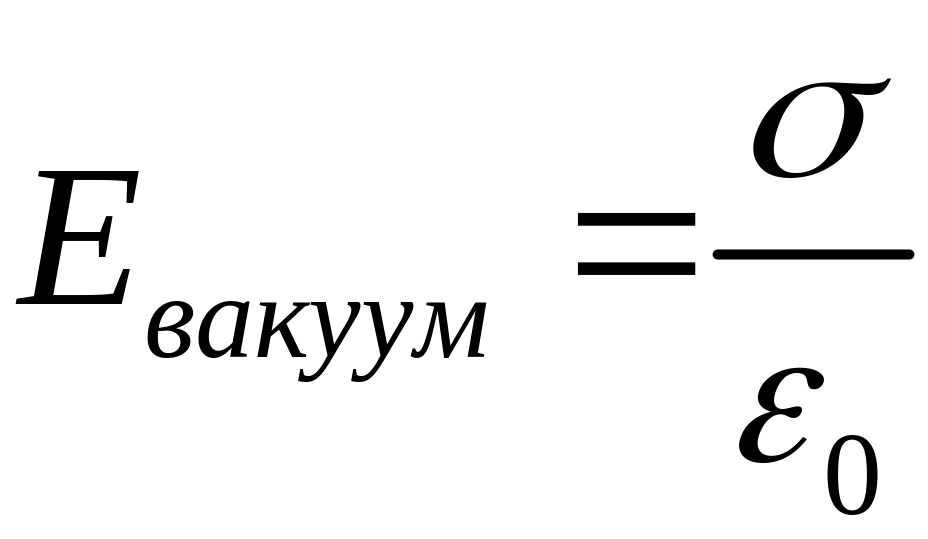2а) - электрическое смещение .

(**)

Так как (следует из (*))

, а . Из (*) и (**) получаем

.

Т.к. , значит, электрическое смещение у поверхности проводника равно непосредственно поверхностной плотности заряда , т.е. величина сместившегося внутри проводника в расчете на единицу поверхности. Этим объясняется происхождение термина «электрическое смещение».

49. Поле равномерно заряженного бесконечного цилиндра

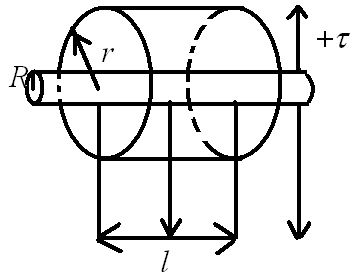
Бесконечный цилиндр радиуса

заряжен равномерно с линейной

плотностью ( 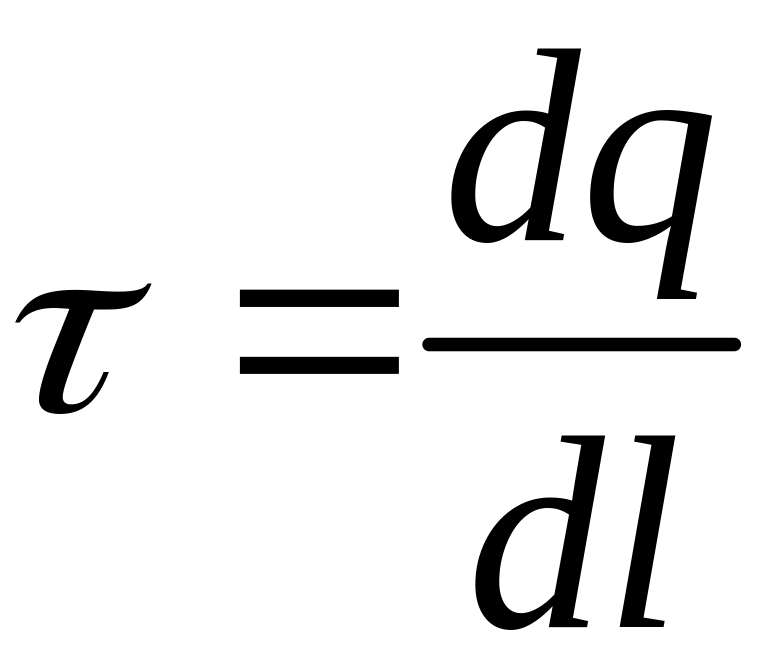, , - заряд,

приходящийся на единицу длины). ***Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией***

Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим заряженный цилиндр радиуса и высотой . Поток вектора сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен . По теореме Гаусса (***Теорема Гаусса Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на : ***), при , .

Тогд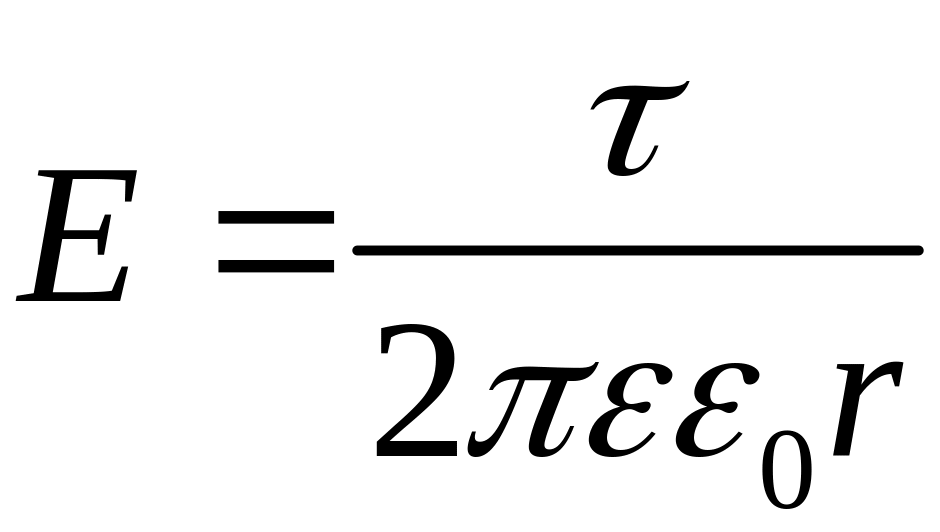а , а .

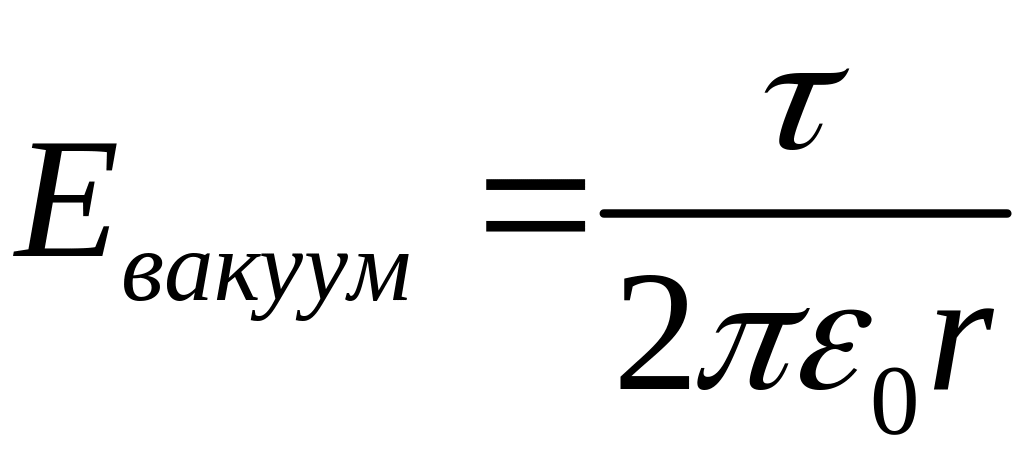Если , то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области напряженность . Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением , внутри же его поле отсутствует.

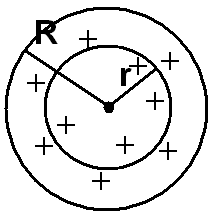
50. Поле объемно заряженного шара.

Шар радиуса с общим зарядом заряжен равномерно с плотностью (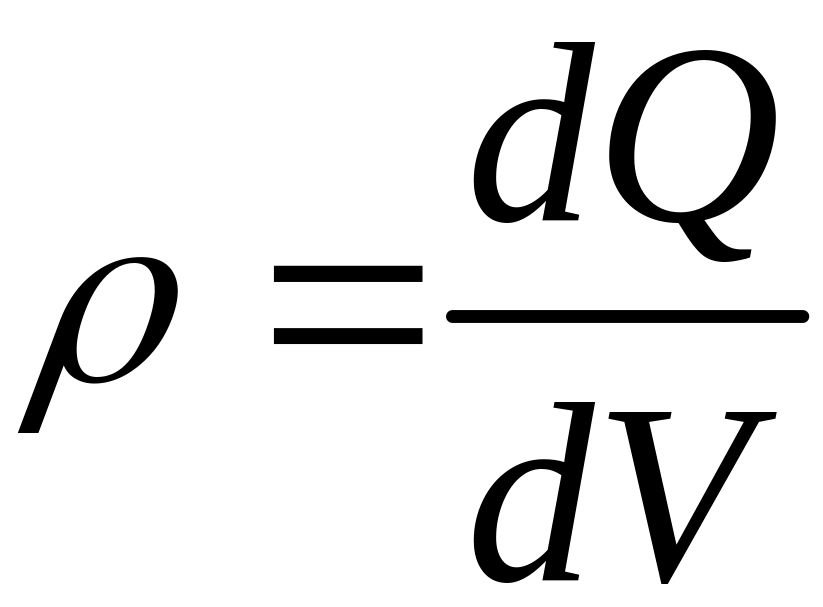 - заряд, приходящийся на единицу объема).

.

Вне шара напряженность поля получится 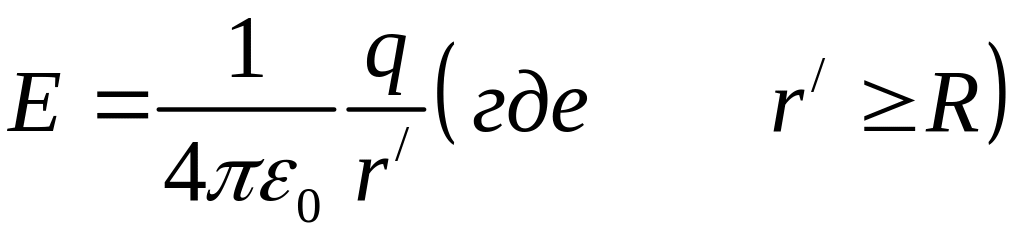. Внутри же шара напряженность получится другая. Сфера радиуса охватывает заряд .

.

.

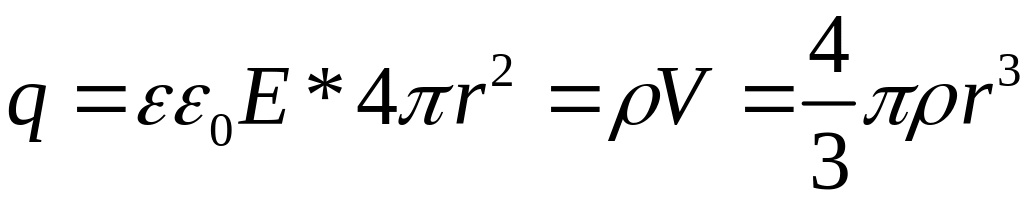
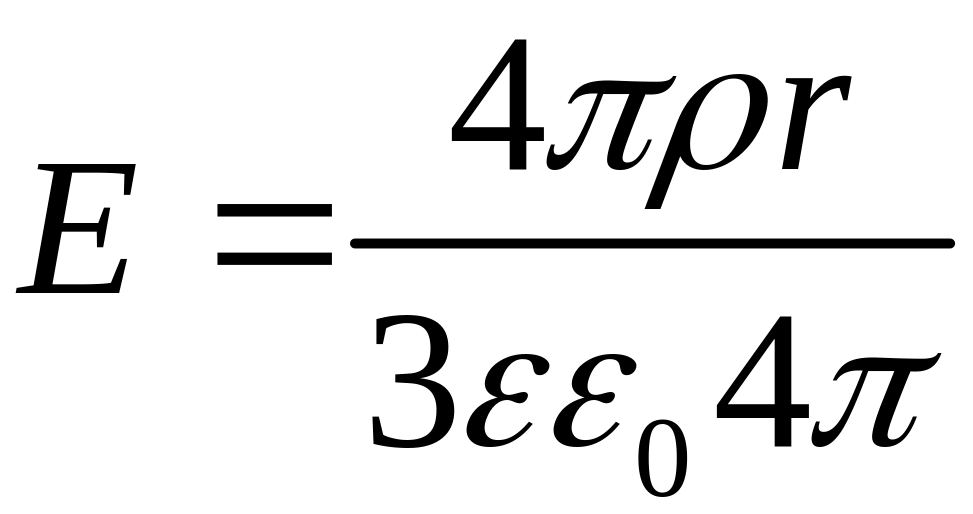
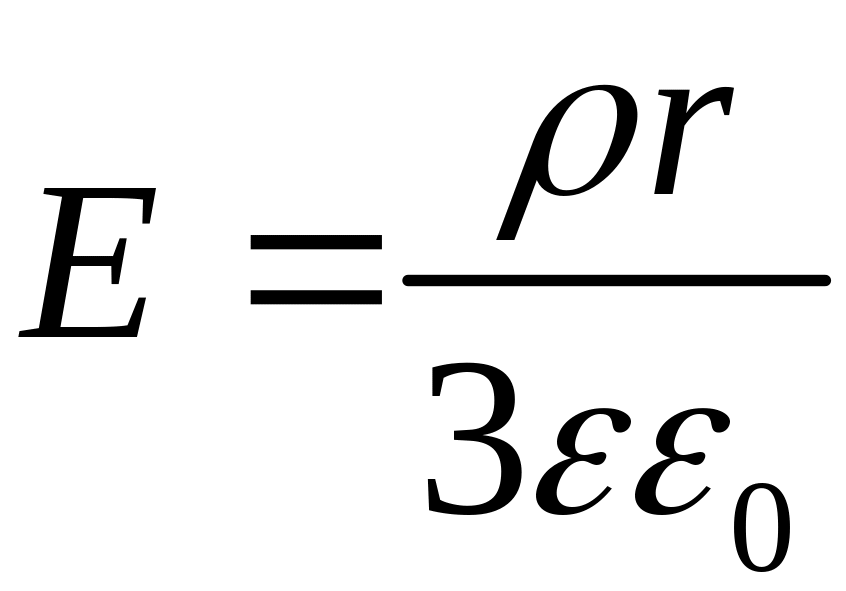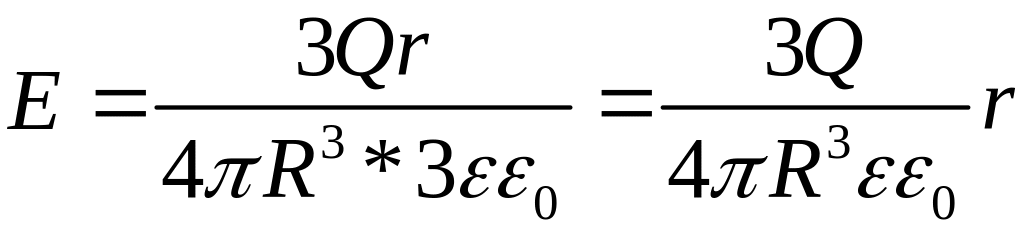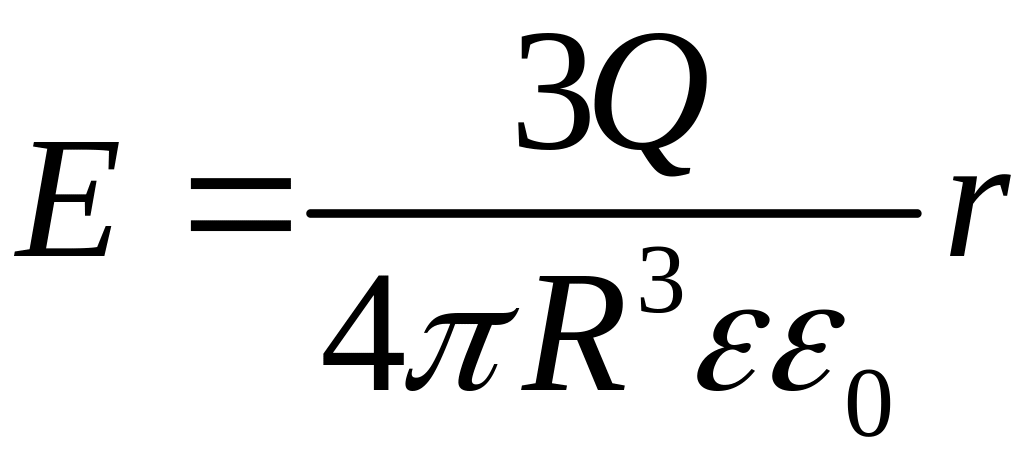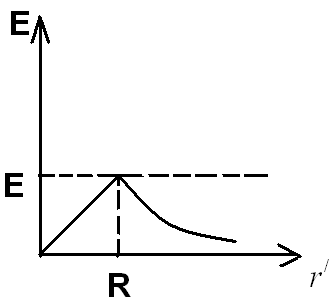
Т.о. напряженность поля вне равномерно заряженного шара описывается формулой , а внутри его изменяется линейно с расстоянием согласно выражению . График зависимости от для рассмотренного случая: