
РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ФУРЬЕ
Сходимость ряда Фурье. Явление Гиббса
Каждой абсолютно интегрируемой на отрезке* [—π, π] функции f(x) можно поставить в соответствие ее тригонометрический ряд Фурье:

Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера — Фурье:
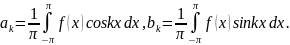
Справедливо следующее утверждение. Если функция f(x) кусочно-гладкая на отрезке[—π, π], то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если

сумма тригонометрического ряда Фурье, то

для любого X ϵ [—π, π] и

Обозначим
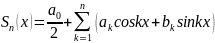 n-ю
частичную сумму ряда Фурье кусочно-гладкой
на отрезке [—π,
π] функции
f(x).
Тогда утверждение теоремы можно записать
в виде:
n-ю
частичную сумму ряда Фурье кусочно-гладкой
на отрезке [—π,
π] функции
f(x).
Тогда утверждение теоремы можно записать
в виде:
 ,
если f(x) непрерывна в точке х0;
,
если f(x) непрерывна в точке х0;
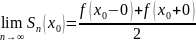 , если f(x) терпит разрыв первого рода
(скачок) в точке х0.
, если f(x) терпит разрыв первого рода
(скачок) в точке х0.
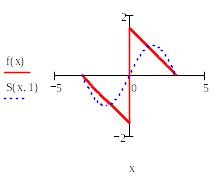
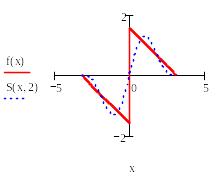
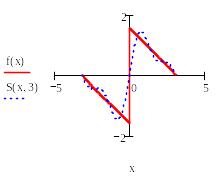
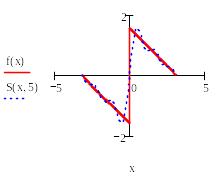
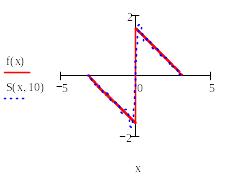
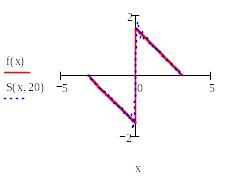
Ниже приведен фрагмент рабочего документа Mathcad с графиком функции*

и графики частичных сумм Sn(x) ее ряда Фурье.
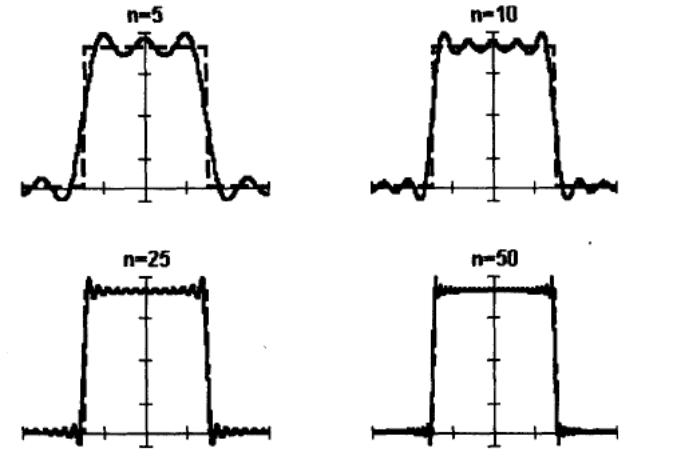
На
графиках видно, как сходятся частичные
суммы ряда Фурье. В окрестности точек
непрерывности функции f(x) разность между
значением функции в точке х и значением
частичной суммы ряда в этой точке
стремится к нулю при n
→
 ,
что полностью соответствует теории,
поскольку в этом случае
,
что полностью соответствует теории,
поскольку в этом случае
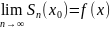 .
Видно также, что разность Sn(x)
— f(x) стремится к нулю тем скорее, чем
дальше от точек разрыва функции
расположена точка х. В окрестности точек
разрыва x0
=
.
Видно также, что разность Sn(x)
— f(x) стремится к нулю тем скорее, чем
дальше от точек разрыва функции
расположена точка х. В окрестности точек
разрыва x0
=
 функции f(x) частичные суммы Фурье ведут
себя иначе. При этом видно, что, хотя
функции f(x) частичные суммы Фурье ведут
себя иначе. При этом видно, что, хотя

существуют
такие последовательности un
→
x0
+ 0 и vn
→
x0
- 0, что пределы Sn(un)
и Sn(vn)
при n
 различны и
оба отличаются
от
различны и
оба отличаются
от
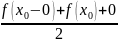 .
.
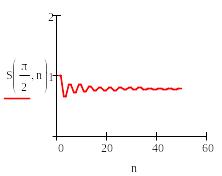
Эта особенность поведения частичных сумм Фурье в окрестности точек разрыва называется явлением Гиббса. Явление Гиббса состоит в том, что для некоторых функций f(x) в точке x0 ее скачка существуют такие значения α, что

Это утверждение не противоречит теории, поскольку у Гиббса рассмотрен предел Sn(xn), а в теореме — Sn(x).
ЗАДАНИЕ 3.33
Исследуйте графически поведение частичных сумм ряда Фурье заданной функции f(x). Вычислите значение суммы ряда Фурье в указанных точках и в точках —π, π.
Порядок выполнения задания
1. Установите автоматический режим вычислений и режим отображения результатов по горизонтали.
2. Определите заданную функцию переменной х и постройте ее
3. Найдите выражения для коэффициентов Эйлера — Фурье и для частичной суммы ряда как функции S(x,n) переменных x и π.
4. Положив n = 50, вычислите коэффициенты Эйлера — Фурье и частичную сумму ряда S(x, 50).
5. Постройте графики S(х,1), S(x,2), S(x,5), S(x,10), S(x,50) и сравните их между собой и с графиком f(x).
6. Вычислите значения 5(х,1), S(x,2), S(x,5), S(x, 10), S(x,50) в указанных точках и в точках —π, π.
7. Для х = x0, где х0 — точка непрерывности функции, постройте график частичной суммы S(x,n) как функции переменной n.
Пример выполнения задания
Исследуйте графически поведение частичных сумм ряда Фурье для функции

Постройте
графики частичных сумм для n
= 1, 2, 5,10, 20, 50. Вычислите значения частичных
сумм ряда Фурье для n
= 10, 20, 50 в точках X = —π,
0,
 π.
π.
Примерный вариант выполнения задания приведен ниже.

![]()
![]()
Вычисление коэффициентов Фурье по формулам Эйлера — Фурье
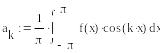
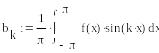
Вычисление частичной суммы ряда Фурье
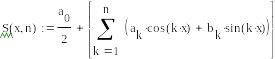
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Указание.
Для того чтобы определить функцию,
заданную разными аналитическими
выражениями на разных промежутках,
лучше всего поступить следующим образом.
Щелкнув в панели математических
инструментов по кнопкам
![]()
![]() откроите
соответствующие панели и разместите
их на рабочем документе, как показано
на рис. 3.25. Введите имя функции переменной
х, щелкните в панели калькулятора по
кнопке присваивания
откроите
соответствующие панели и разместите
их на рабочем документе, как показано
на рис. 3.25. Введите имя функции переменной
х, щелкните в панели калькулятора по
кнопке присваивания
![]() ,
затем в панели программирования — по
кнопке Add Llne . В рабочем документе справа
от знака присваивания появится
вертикальная черта с двумя помеченными
строками для ввода. Перейдите в первую
строку и щелкните по кнопке lf , введите
слева от слова if выражение для вычисления
функции, а справа — соответствующее
ограничение на аргумент. При вводе
выражений используйте кнопки панелей
калькулятора, знаков отношений и
греческого алфавита. Аналогично введите
выражение во второй строке. Сохраните
выражения для коэффициентов Фурье в
виде векторов а и b.
Для этого определите размерность вектора
n
равной 50 и определите диапазон изменения
номера к компонент векторов а и b
от 0 до п. Для того чтобы найти выражение
для коэффициента Фурье аk,
введите с клавиатуры а, знак нижнего
индекса (нажмите клавишу <[>), введите
в позиции нижнего индекса k,
вернитесь в основную строку, введите
знак присваивания и выражение для
коэффициента. Аналогично определите
выражения для коэффициентов bk.
Частичную сумму ряда определите как
функцию двух переменных - n
и х. Прежде чем строить графики частичных
сумм, задайте таблицу значений аргумента
х на отрезке [—π,
π]
с некоторым шагом (в рассмотренном
выше примере выбран шаг π/100).
Численное исследование частичных сумм
состоит в сравнении значений частичных
сумм для различных N со значениями
функции на концах отрезка, в точке скачка
и в точке непрерывности. Введите имя
функции (частичной суммы), указав в
скобках нужное значение аргумента, и
нажмите клавишу <=>, в результате на
экране будет отображено значение функции
в точке. Полезную информацию о поведении
частичных сумм дает график зависимости
значений от n
,
затем в панели программирования — по
кнопке Add Llne . В рабочем документе справа
от знака присваивания появится
вертикальная черта с двумя помеченными
строками для ввода. Перейдите в первую
строку и щелкните по кнопке lf , введите
слева от слова if выражение для вычисления
функции, а справа — соответствующее
ограничение на аргумент. При вводе
выражений используйте кнопки панелей
калькулятора, знаков отношений и
греческого алфавита. Аналогично введите
выражение во второй строке. Сохраните
выражения для коэффициентов Фурье в
виде векторов а и b.
Для этого определите размерность вектора
n
равной 50 и определите диапазон изменения
номера к компонент векторов а и b
от 0 до п. Для того чтобы найти выражение
для коэффициента Фурье аk,
введите с клавиатуры а, знак нижнего
индекса (нажмите клавишу <[>), введите
в позиции нижнего индекса k,
вернитесь в основную строку, введите
знак присваивания и выражение для
коэффициента. Аналогично определите
выражения для коэффициентов bk.
Частичную сумму ряда определите как
функцию двух переменных - n
и х. Прежде чем строить графики частичных
сумм, задайте таблицу значений аргумента
х на отрезке [—π,
π]
с некоторым шагом (в рассмотренном
выше примере выбран шаг π/100).
Численное исследование частичных сумм
состоит в сравнении значений частичных
сумм для различных N со значениями
функции на концах отрезка, в точке скачка
и в точке непрерывности. Введите имя
функции (частичной суммы), указав в
скобках нужное значение аргумента, и
нажмите клавишу <=>, в результате на
экране будет отображено значение функции
в точке. Полезную информацию о поведении
частичных сумм дает график зависимости
значений от n

Рис. 3.25. Панели инструментов для ввода функции с использованием панели программирования
Приближение функций. Минимальное свойство коэффициентов Фурье
Функция
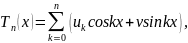
где
Uk,
Vk
— произвольные числа, называется
тригонометрическим многочленом.
Тригонометрическим
многочленом наилучшего приближения
n-й
степени
функции f(x) на отрезке [—π,
π]
называется тригонометрический многочлен
Рn(х)
 среднеквадратичное отклонение σn(х)
которого от функции f(x) минимально:
среднеквадратичное отклонение σn(х)
которого от функции f(x) минимально:
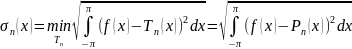
Для любой ограниченной интегрируемой на [—π, π] функции f(x) частичная сумма Sn(x) ее ряда Фурье является тригонометрическим многочленом, наилучшего приближения n-й степени.
ЗАДАНИЕ 3.34
Найдите для заданного значения погрешности е тригонометрический многочлен наилучшего приближения функции f(x) и наименьшей степени со среднеквадратичным отклонением, меньшим Ɛ. Постройте график зависимости среднеквадратичного отклонения от степени многочлена.
