Графы схем электрических цепей.

Граф –совокупность отрезков произвольной длины,формы, называемых ветвями (ребрами) и точек их соединений, называемых узлами (вершинами)

Электрическая цепь графически отображается электрической схемой, на которой показаны все элементы и порядок их соединений, также направления токов (рис1)

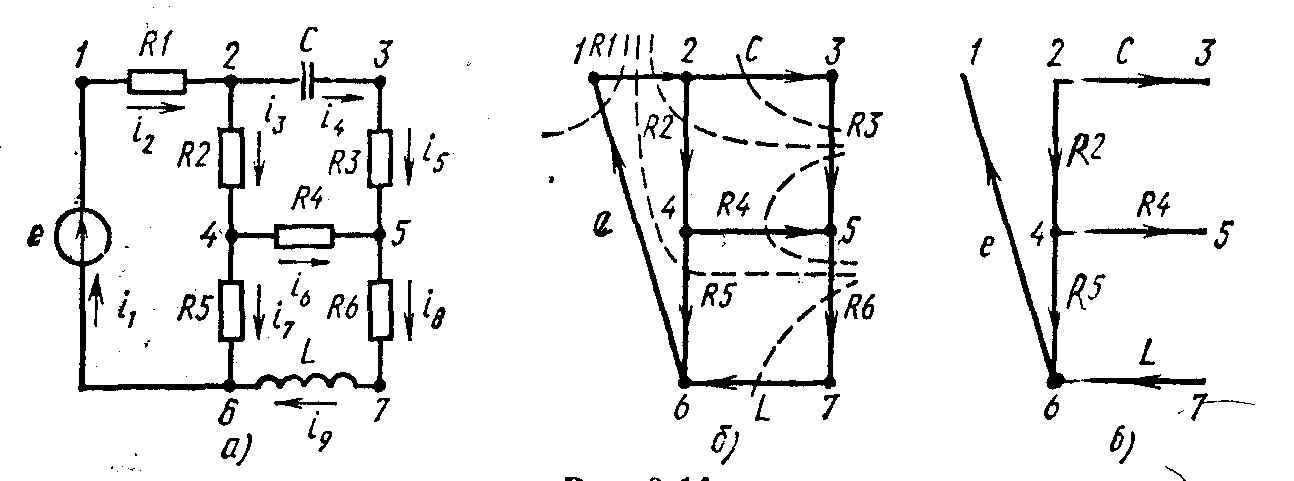
Рис. 1. а-схема электрической цепи, б – связный граф, в – дерево графа.

Замкнутый путь, у которого начальные и конечные узлы совпадают называются контуром.

Либо замкнутый ток, проходящий через некоторое количество ветвей (части графа) называется контуром. Связный граф – это граф между любыми двумя узлами которого существует, по крайне мере, один путь. Деревом связного графа называется связный подграф, включающий все узлы графа, но не содержащий ни одного контура. На каждом графе цепи можно найти несколько деревьев. Ветви графа, вошедшие в дерево, называются ветвями дерева. Ветви не вошедшие – связями (главные ветви, хорды). Сумма ветвей и связей равно общему числу ветвей. Каждое из деревьев графа, содержащего р ветвей и q узлов, имеет m=q-1ветвей дерева и n=p-q+1 главных ветвей (связей). Добавление к дереву графа любой связи образует контур. Сечением связного графа называется минимальная совокупность ветвей графа, при удаления которых граф распадается на две изолированные части, одна из которых может быть узлом. Главным сечением графа называется сечение, в которое входит только одна ветвь выбранного дерева. Остальные ветви, входящие в главное сечение, являются связями. Число главных сечений равно числу ветвей дерева: m = q – 1.

Определение числа независимых узлов и контуров

Чтобы получить независимые уравнения достаточно, чтобы каждое уравнение отличалось от остальных хотя бы одной переменной. Так, для линейной независимости уравнений, составленной на основании 1-го закона Киргофа, достаточно, чтобы каждое уравнение баланса токов отличалось от других уравнений хотя бы одним током или, что то же самое, одной ветвью. Каждому дереву графа можно поставить в соответствие m = q – 1 главных сечений и, следовательно, m = q – 1 линейно независимых уравнений баланса токов.

Для линейной независимости уравнений, составленной на основе 2-го закона Киргофа, достаточно, чтобы каждое из этих уравнений отличалось от остальных хотя бы одним напряжением. Следовательно, каждый контур должен отличаться от остальных хотя бы одной ветвью. Этому требованию удовлетворяет система главных контуров, которые отличаются от других хотя бы одной связью: n = p – q + 1, число независимых контуров равно числу связей. Таким образом, общее число независимых уравнений оказывается равным числу ветвей цепи: m + n = (q – 1) + (p – q + 1) = p.

Для схемы, показанной на рис. 1, можно составить 9 независимых уравнений. В этой цепи 9 ветвей (9 токов) и 7 узлов, поэтому по закону Киргофа для токов можно составить 6 независимых уравнений для токов m = q – 1 = 7 – 1 = 6 уравнений:

1). –i₁ + i₂ + 0; 2) –i₂ + i₃ = i₃ = 0; 3) –i₄ + i₅ = 0; 4) –i₃ + i₆ + i₇ = 0; 5) –i₅ –i₆ +i₈ =0; 6) –i₈ + i₉ = 0.

По второму закону Кирхгофа можно составить три независимых уравнений для контуров

n = p – q + 1 = 9 – 7 + 1: 1) u_R1 + u_R2 +u_R5 = e; 2) u_c + u_R3 – u_R4 – u_R2 = 0; 3) u_R4 + u_R6 – u_L –u_R5.

Свойство уравнений, полученных на основе законов Кирхгофа, можно показать на примере последовательного и параллельного соединений элементов R, L, C.

Рис2.а) Последовательное соединение источника и элементов RLC, б) Параллельное соединение источника и элемента RLC.

На первом рисунке соединение элементов образует один замкнутый контур, поэтому по закону Кирхгофа для напряжений:

L=

Т.к. через все элементы протекает один и тот же ток, то интегро-дифференциальное

E = iR + L

Т.е. полученное уравнение содержит одну переменную величину - ток в контуре.

Параллельное соединение источника и элементов (второй рисунок) образует цепь с двумя узлами, поэтому по закону Кирхгофа для токов:

Т.к. на всех элементах цепи падает одно и тоже напряжение, то

т.е. получено интегро-дифференциальное уравнение относительно U.

Для более сложных цепей получаются системы интегро-дифференциальных уравнений.

Расчет сложных (разветвленных) схем проводят на основе законов Кирхгофа, с помощью которых можно рассчитать любую электрическую схему. Однако часто их непосредственное применение приводит к составлению слишком большого числа линейных уравнений, а значить, и большему объему вычислений. Чтобы хотя бы частично обойти эти трудности, были разработаны методы, упрощающие эти расчеты. Упрощение достигается двумя способами: 1) введением дополнительных расчетных величин, позволяющих уменьшить число уравнений, 2) предварительным преобразованием анализируемой схемы. К методам первой группы относится метод контурных токов и метод узловых потенциалов, к методам второй группы – метод наложения (суперпозиции), метод эквивалентного источника, метод взаимности, преобразования треугольника в звезду, звезды в треугольник и др. При выборе метода расчета разветвлений схемы в каждом конкретном случае исходят из постановки задачи, причем выбирают тот метод, который позволяет провести расчет быстрее, проще и нагляднее. Коротко охарактеризуем два метода: метод контурных токов и метод наложения.

Метод контурных токов основан на втором законе Кирхгофа. Согласно этому методу расчет проводят в два этапа. На первом вводится понятие некоторых так называемых контурных токов. В отличие от токов в ветвях под контурным понимают ток в выделенном контуре. На втором этапе определяют токи в ветвях, которые представляют собой алгебраическую сумму токов, протекающих в контурах, в состав которых входит данная ветвь. Важно, что выделенные в схеме контуры независимы, то есть каждый из них содержит ветвь, ранее не входившую ни в один предшествующий в процессе выбора контур.

Для нахождения контурных токов составляют и решают систему линейных уравнений контурных токов. Число уравнений такой системы равно числу независимых контуров схемы; оно всегда меньше числа ветвей. Следовательно, и число уравнений в случае метода контурных токов всегда меньше числа уравнений в случае непосредственного применения законов Кирхгофа.

Пусть нужно рассчитать токи в схеме, приведенной на рис. 3. Сначала выберем независимые контуры и установим положительные направления контурных токов в каждом из них по направлению часовой стрелки. Пользуясь вторым законом Кирхгофа, составим уравнение для каждого контура:

Для первого R₁i₁+R₂(i₁-i₁₁) = e₁

Для второго R₃i₁₁+R₂(i₁₁-i₁)+R₄(i₁₁-i_{111) = 0;}

Для третьего R₅i₁₁₁+R₄(i₁₁₁-i₁₁) = e₂.

В результате получим систему трех уравнений (в случае непосредственного применения законов Кирхгофа их было бы пять). Решив ее, получим значения контурных токовi₁, i₁₁, i₁₁₁, что позволить найти токи в отдельных ветвях схемы:

i₁=i₁; i₂=i₁₁; i₃=i₁₁; i₄=i₁₁-i₁₁₁; i₅=i₁₁₁.

Особенно удобно применять метод контурных токов для расчета схем с источником тока. Например, в случае схемы рис.4 в качестве первого контура целесообразно выбрать источник ЭДС, резистивные элементы R₂ и R₃, а в качестве второго – источник тока и R₁, R₂. В этом случае ток второго контура оказывается заданным (i₁=J) и для определения токов во всех ветвях нужно рассчитать только один контурный ток i₁₁, то есть составить всего одно уравнение.

(R₂+R₃)i₁₁-R₂J = e,

из которого определяется ток i₁₁, а затем и токи во всех ветвях:

i₁=J; i₂=J-i₁₁; i₃=i₁₁.

Рис.3. К расчету резистивной схемы Рис.4. К расчету резистивной

методом контурных токов. схемы с источником тока.

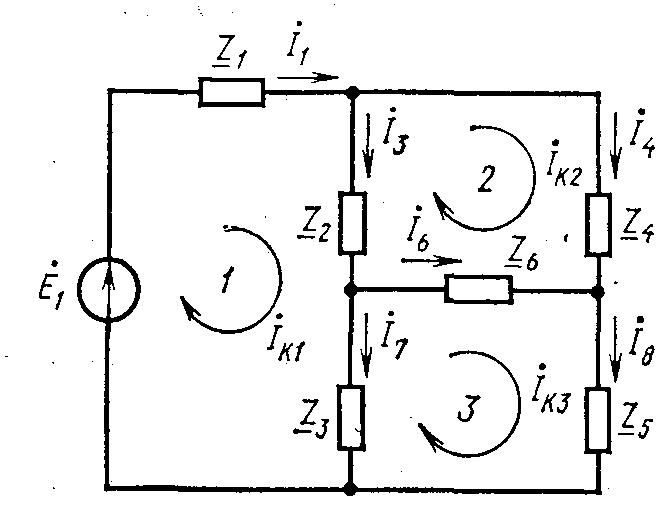В цепи , приведенной на _рис. 5., могут быть три независимых контурных тока I_k1, I_k2 и I_k3 , протекающие в контурах 1, 2, 3, обозначенных стрелками. Токи в элементах этой цепи связаны с контурными токами следующими зависимостями:

I₁ = I_k1; I₃ = I_k3 – I_k2 ; I₇ = I_k1 – I_k3;

Рис. 5.

I₄ = I_k2; I₈ = I_k3; I₆ = I_k3 – I_k2. (5.1)

Подставив эти токи в формулу, составленные по закону Кирхгофа для напряжений, после группировки получим систему уравнений:

(Z₁+Z₂+Z₃) I_k1 – Z₂ I_k2 –Z₃ I_k3 = E₁;

–Z₂ I_k1+(Z₁+Z₂+Z₃) I_k2–Z₆I_k3=0;

–Z₃I_k1–Z₆I_k2+(Z₁+Z₂+Z₃) I_k3=0 (5.2)

В этой системе три неизвестных контурных тока и, следовательно, система может быть решена. После нахождения контурных токов токи в элементах рассчитывают по формулам (5.1).

Четырехполюсники, основные определения.

Большинство радиоэлектронных устройств (например, усилители, преобразователи и другие устройства) предназначены для передачи электрических сигналов. Характерной особенностью таких устройств, рассматриваемых с точки зрения теории цепей, является наличие двух пар зажимов, с помощью которых они могут быть соединены с внешними цепями. Поэтому четырехполюсником будем считать электронную цепь с двумя парами зажимов, включаемую таким образом, что через каждую пару зажимов протекают попарно равные и противоположно направленные токи:

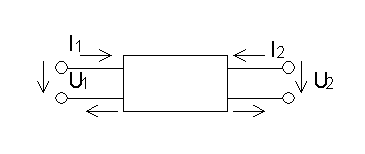
Рис. 7.1

Уравнения четырехполюсника устанавливают взаимную связь между токами и напряжениями во внешних контурах U₁, I₁ и U₂ , I₂. Если предположить, что две из перечисленных величин представляют воздействия (аргументы), то остальные две – реакцияю (функции) четырехполюсника. Возможные варианты воздействий, реакций и их взаимная связь представлены ниже:

Варианты	1	2	3	4	5	6
Воздействия	I1, I2	U1, U2	U2, I2	U1, I1	I1, U2	U1, I2
Реакции	U1, U2	I1, I2	U1, I1	U2, I2	U1, I2	U2, I1
Параметры	Z	Y	A	B	H	G

Например, для первого варианта, когда заданы токи, напряжения равны: U₁=Z₁₁I₁+Z₁₂I₂; U₂=Z₂₁I₁+Z₂₂I₂ (7,1)

Если заданы напряжения, то токи равны::

I₁= Y₁₁U₁+Y₁₂U₂; I₂=Y₂₁U₁+Y₂₂U₂ (7,2)

Здесь параметры Z и Y имеют размерности сопротивлений и проводимостей, соответственно. Если в качестве аргументов принять входной ток I₁ и выходное напряжение U₂ , тогда:

U₁=h₁₁I₁+h₁₂U₂; I₂=h₂₁I₁+h₂₂U₂ (7,3)

В этом случае h-параметры имеют разные размерности. h₁₁ – входное сопротивление, которое измеряется при короткозамкнутом выходе. h₁₂ – обратный коэффициент передачи напряжения при разомкнутом входе. h₂₁ – прямой коэффициент передачи тока при короткозамкнутом выходе. h₂₂ – выходная проводимость при разомкнутом входе. h – параметры используются при анализе транзисторных схем.