ПЛАСТИЧЕСКОЕ ДЕФОРМИРОРВАНИЕ МАТЕРИАЛОВ.

Физические основы. Экспериментальные методы. Математическое моделирование.

Глава 4. Жесткопластическое деформирование при условии плоской деформации

1. Плоская деформация. Жесткопластическое приближение. Основные уравнения.

4.1.1. Плоская деформация.

Плоской деформацией называется такое деформированное состояние тела, при котором смещения всех частиц тела параллельны одной плоскости. Эту плоскость выбирают в качестве плоскости . Таким образом, плоская деформация в трехмерном теле определяется следующим условием, наложенным на перемещения:

, , . (4.1)

Такое состояние характерно для длинных призматических тел из однородного изотропного материала, нагруженных по нормали к боковой поверхности силами, не зависящими от .

4.1.2. Жесткопластическая модель материала.

Аналитическое решение задач плоского деформирования для упругопластического тела затруднительно, однако существует приближенный метод, в рамках которого тело рассматривается как жесткопластическое, то есть деформирование происходит только в тех областях, где выполнено условие текучести. Условие текучести – условие перехода материала в пластическое состояние может, например, иметь вид

(4.2)

– материал начинает пластически деформироваться, если максимальное касательное напряжение достигло экспериментально определяемого предела текучести при на сдвиге.

Такое упрощение вносит в решение задач погрешность, плохо поддающуюся оценке, но если пластические деформации локализованы в некоторой достаточно четко определяемой области и велики настолько, что в сравнении с ними упругими деформациями можно пренебречь, жесткопластическое тело является достаточно близкой моделью реального. Такая ситуация реализуется в технологических задачах с установившейся текучестью, к которым относятся, например, прокатка, волочение проволоки, штамповка. Для этих процессов получаемые решения показывают удовлетворительное согласование с экспериментальными данными, хотя, к сожалению, не всегда бывают однозначны. Кроме того, жесткопластическая модель дает возможность получать оценки предельных нагрузок.

4.1.3. Главные напряжения при плоской деформации.

Считается, что пластические деформации не могут быть вызваны гидростатическим нагружением, поэтому пластическую составляющую тензора деформаций связывают с девиатором тензора напряжений соотношениями вида или , о которых подробно сказано в следующей главе. Поскольку , из этих соотношений следует, что

, (4.3)

где – гидростатическое давление.

При плоской деформации напряженно-деформированное состояние во всех сечениях будет одинаковым и компоненты его не будут зависеть от . При этом , а значит и из уравнения

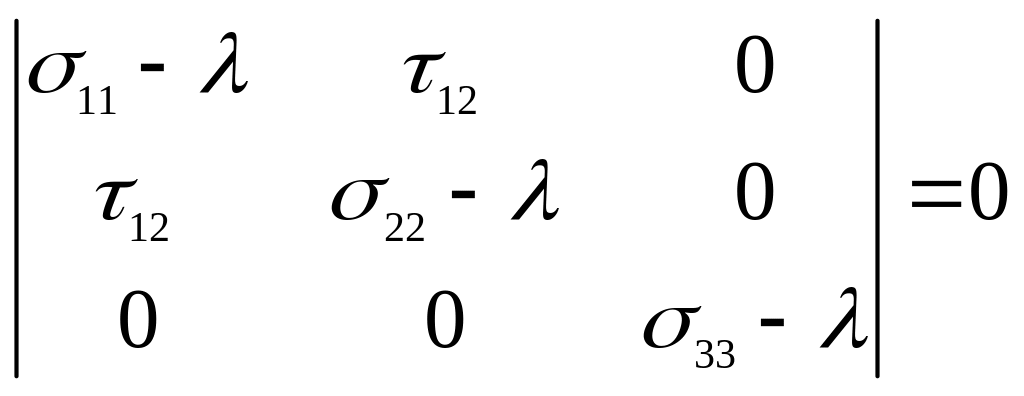(4.4)

видим, что является одним из главных напряжений. Обозначим его как , отказавшись от обычно применяемого правила нумерации главных напряжений, приведенного в прошлой главе.

Найдем два оставшихся главных напряжения:

, (4.5)

, , . (4.6)

Поскольку максимальное касательное напряжение определяется выражением

, (4.7)

то главные напряжения запишем в виде

, , . (4.8)

Здесь – напряжение чистого сдвига.

Направляющие косинусы первого главного направления находим из системы

(4.9)

Зная первое главное направление, мы можем найти направления площадок, на которых действуют максимальные касательные напряжения, на том основании, что эти направления составляют с главным угол .

4.1.4. Основные уравнения в напряжениях для жесткопластического материала при плоской деформации.

Когда среда находится в состоянии идеальной пластичности, выполнено условие (4.2), которое из (4.7) можно переписать в виде

, (4.10)

и к этому соотношению добавить уравнения равновесия с нулевыми объемными силами (поскольку вес в рассматриваемых задачах не играет заметной роли, а ускорения отсутствуют):

. (4.11)

Если к этому добавить граничные условия для напряжений, у нас будет полная система уравнений для определения напряженного состояния независимо от деформаций.

Для полной задачи теории пластичности нам нужны еще соотношения, связывающие напряжения с деформациями, например, вида . Однако, если использовать рассматриваемую упрощенную модель для нахождения экстремальных нагрузок, эти соотношения нам не понадобятся, поэтому здесь мы ограничимся уравнениями в напряжениях.

Компоненты двумерного тензора напряжений выражаются через главные напряжения следующим образом:

(4.12)

Поскольку , , систему (4.12) можно переписать в простом виде:

, (4.13)

где . Справедливость этих уравнений автоматически означает удовлетворение условия текучести. Подставив (4.13) в (4.11), получим следующую систему дифференциальных уравнений в частных производных от неизвестных функций и :

, (4.14)

определяющую напряженное состояние жесткопластического твердого тела при плоской деформации.