23. Объемы и площади поверхности тел вращения

23.1. Объем и площадь боковой поверхности цилиндра

Найдем объем и площадь боковой поверхности прямого цилиндра радиусом и высотой .

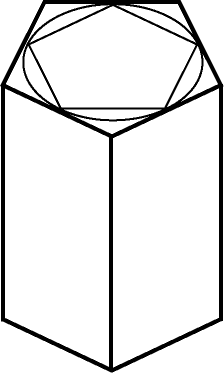
Впишем в цилиндр и опишем вокруг него по прямой -угольной призме с высотой . Тогда объем цилиндра будет заключен в следующих границах:

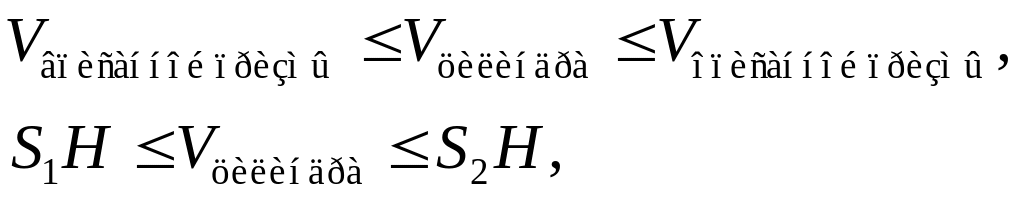
где и – площади оснований вписанной и описанной призмы.

Устремим число к бесконечности. Тогда площади -угольной в основании призм будут стремиться к площади основания цилиндра и по теореме о предельном переходе в неравенствах, получим объем цилиндра равен произведению площади основания на высоту .

Аналогичным образом периметры оснований призм будут стремиться к пирометру основания цилиндра, и площадь боковой поверхности цилиндра равняется произведению длины окружности на высоту .

23.2. Объем и площадь боковой поверхности конуса

Найдем объем и площадь боковой поверхности прямого конуса радиусом и высотой .

Впишем в цилиндр и опишем вокруг него по прямой -угольной пирамиде с высотой . Тогда, проводя рассуждения, аналогичные приведенным в предыдущем разделе, получаем, что объем конуса равен одно трети произведения площади основания на высоту , площадь боковой поверхности равняется произведению полупериметра основания на образующую (которая в пределе совпадает с апофемами вписанной и описанной пирамид) .

23.3. Объем шара и площадь сферы

Объем любого тела, образованного вращением кривой ( ) вокруг оси абсцисс, может быть вычислен по формуле:

.

Поскольку поверхность шара может быть получена вращением половины окружности , то объем шара можно вычислить по вышеприведенной формуле, где при :

Таким образом, объем шара радиусом равняется .

Площадь поверхности любого тела вращения может быть рассчитана по формуле:

.

Тогда для площади поверхности сферы, где имеем:

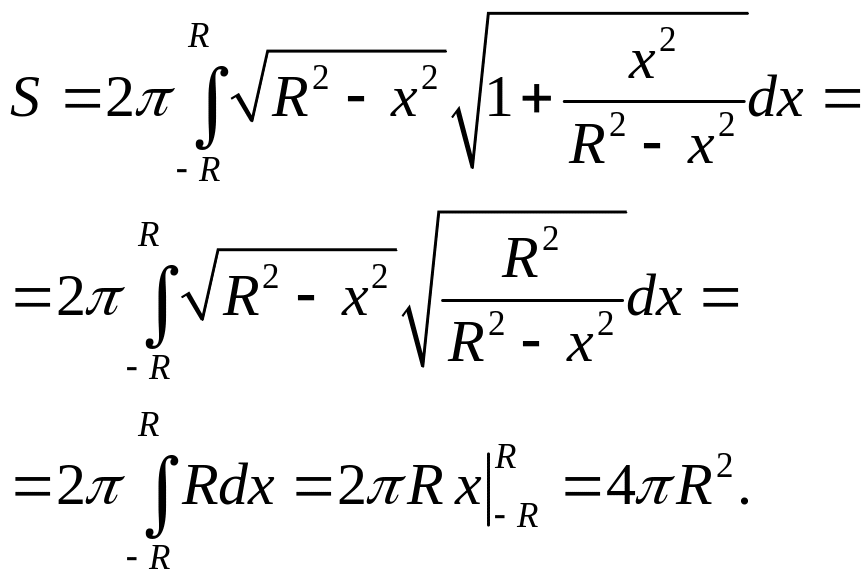
Таким образом, площадь поверхности сферы радиусом равняется .

23.4. Объем шарового сектора и шарового сегмента

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.

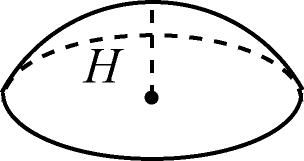
Формула для объема шарового сегмента высотой получается аналогично формуле для объема шара:

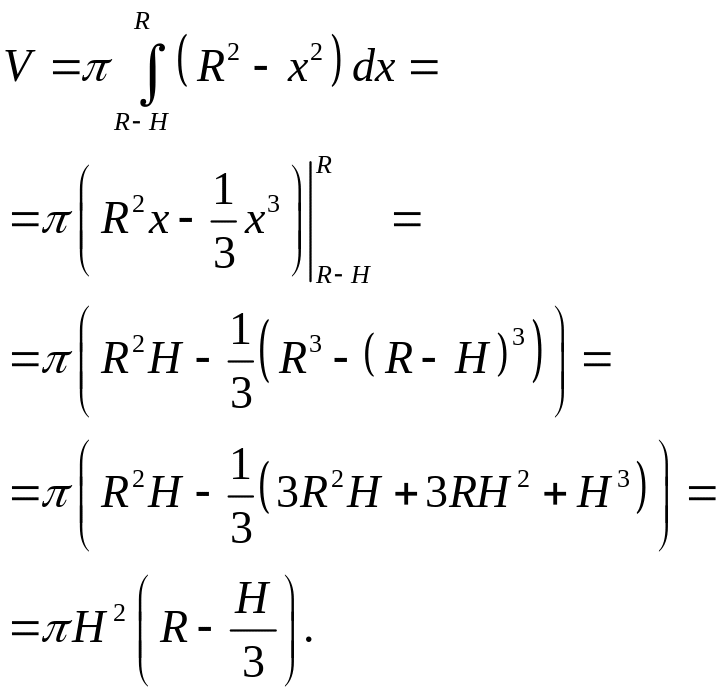
Шаровым сектором называется тело, которое получается из шарового сегмента и конуса, вершиной которого является центр шара, а основание совпадает с основанием сегмента.

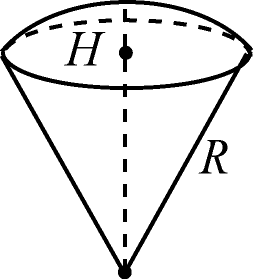
Объем шарового сектора получается как сумма объемов сегмента высотой и конуса с радиусом основания и высотой :

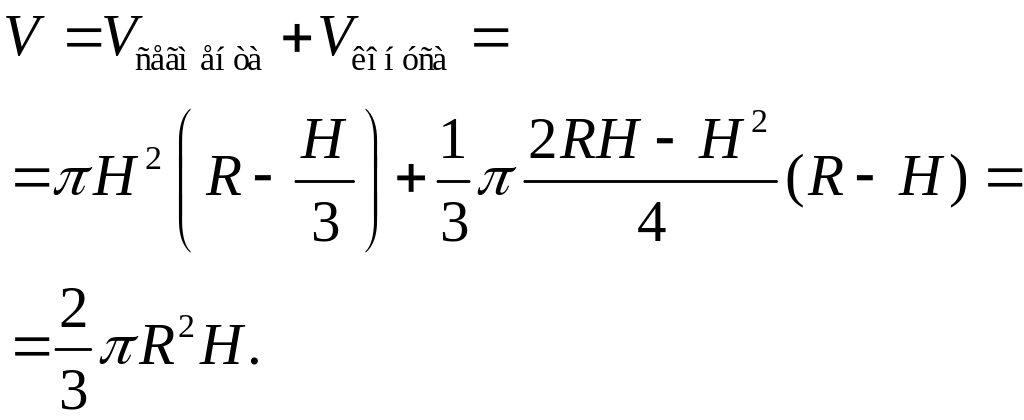
Задачи

1. В цилиндр вписана правильная треугольная призма, а в призму вписан цилиндр. Найти отношение объемов цилиндров.

2. Осевым сечение конуса является равнобедренный прямоугольный треугольник с площадью 9. Найти объем конуса.

3. Равносторонний треугольник вращается вокруг своей стороны . Найти объем полученного тела вращения.

4. Найти объем усеченного конуса с радиусами основани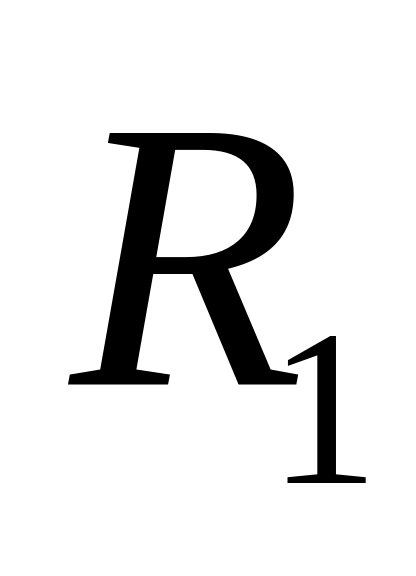й и и высотой .

5. Усеченный конус, у которого радиусы оснований 4 и 22, и равновеликий цилиндр имеют одинаковую высоту. Чему равен радиус основания цилиндра?

6. Из деревянного цилиндра, высота которого равна диаметру основания, выточен наибольший шар. Сколько процентов материала сточено?

7. Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?

8. Диаметр шара, равный 30, является осью цилиндра, у которого радиус основания равен 12. Найти объем части шара, заключенной внутри цилиндра.

9. Шар радиуса 10 цилиндрически просверлен по оси. Диаметр отверстия равен 12. Найти объем тела.

10. Полукруг свернут в коническую поверхность. Найти угол между образующей и осью конуса.

11. Доказать, что полная поверхность равностороннего конуса равновелика поверхности шара, построенного на его высоте как на диаметре.

21