5. Центр тяжести твердого тела

5.1. Определения, свойства и координаты центра тяжести

Центр тяжести  неизменная точка относительно тела. Поэтому его можно определить как точку, обладающую следующим свойством: если твердое тело закреплено в центре тяжести и приведено в состояние равновесия по отношению к некоторой неподвижной системе отсчета, связанной с Землей, то оно будет сохранять это состояние равновесия при любой ориентации тела относительно вертикали.

Сила тяжести элементарного объема равна произведению массы объема на ускорение [ ] (ускорение при размерах тела, достаточно малых по сравнению с Землей, можно считать для всех частей тела одинаковым):

объемная плотность, единица измерения которой в СИ будет [ ] .

В случае однородного тела плотность тела одинакова во всех точках

Если тело представляет собой материальную поверхность, то

поверхностная плотность,  площадь элемента поверхности.

В случае материальной линии (стержень, трос и т.п.)

линейная плотность,  длина элемента линии.

Для однородного тела положение центра тяжести зависит только от геометрической формы тела, а его радиус-вектор и координаты соответственно равны:

(5.1)

Центры тяжести тонкой однородной пластины (рис. 5.2) или оболочки и однородного стержня (рис. 5.5) определяются соответственно формулами

(5.2)

(5.3)

где S  площадь поверхности, L  длина стержня.

Заметим, что в случае однородного поля силы тяжести центр тяжести совпадает с центром масс тела и его положение зависит только от того, как распределена в теле масса. Точка С  центр тяжести (масс)  это геометрическая точка, она может и не принадлежать телу, но всегда с ним связана, например центр тяжести мяча, кольца, и др.

3.2. Методы нахождения центра тяжести

В ряде случаев положение центра тяжести тела можно определить с помощью простых приемов, не прибегая к вычислению интегралов.

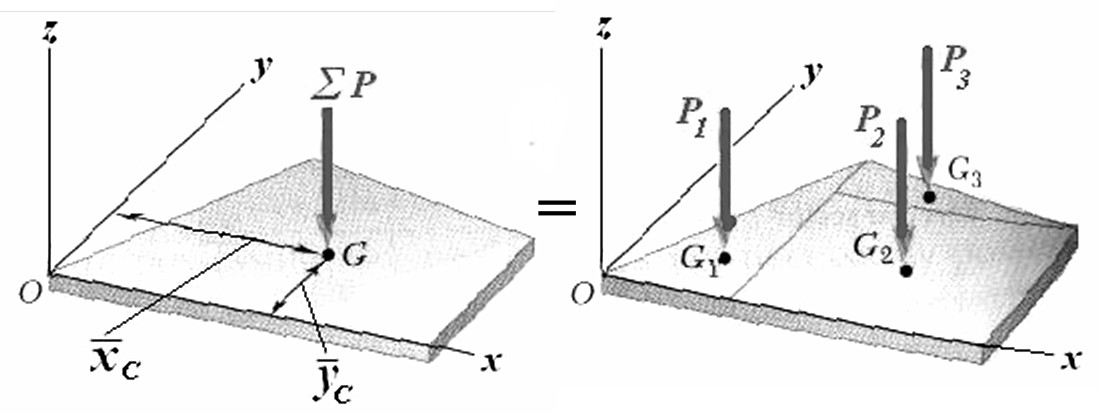
Метод разбиения основан на применении формул для определения положения центра системы параллельных сил (рис. 5.1) в векторной форме или координат точки С в проекциях на оси координат x, y, z

, (5.4)

В формуле (5.4) выражение называется статическим моментом системы параллельных сил относительно центра О, а выражение , входящее во второе равенство (5.4),  статическим моментом системы параллельных сил относительно плоскости Oyz и т.д.

В практике расчетов центра тяжести метод разбиения используют, когда тело можно разбить на ряд отдельных частей, для которых веса и положение центров тяжести известны. Метод разбиения можно наглядно проиллюстрировать на нескольких примерах.

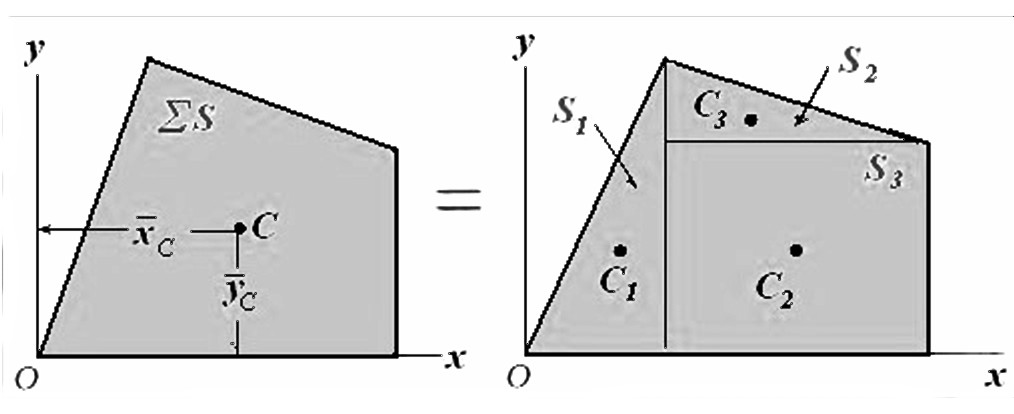
Пример 5.1. Определение центра тяжести однородной пластины (рис.5.1  5.4.

◄

Рис.5.1

◄

Рис. 5.2

Площадь	Форма
	полукруг			
	полый прямоугольник			
	отверстие круга			

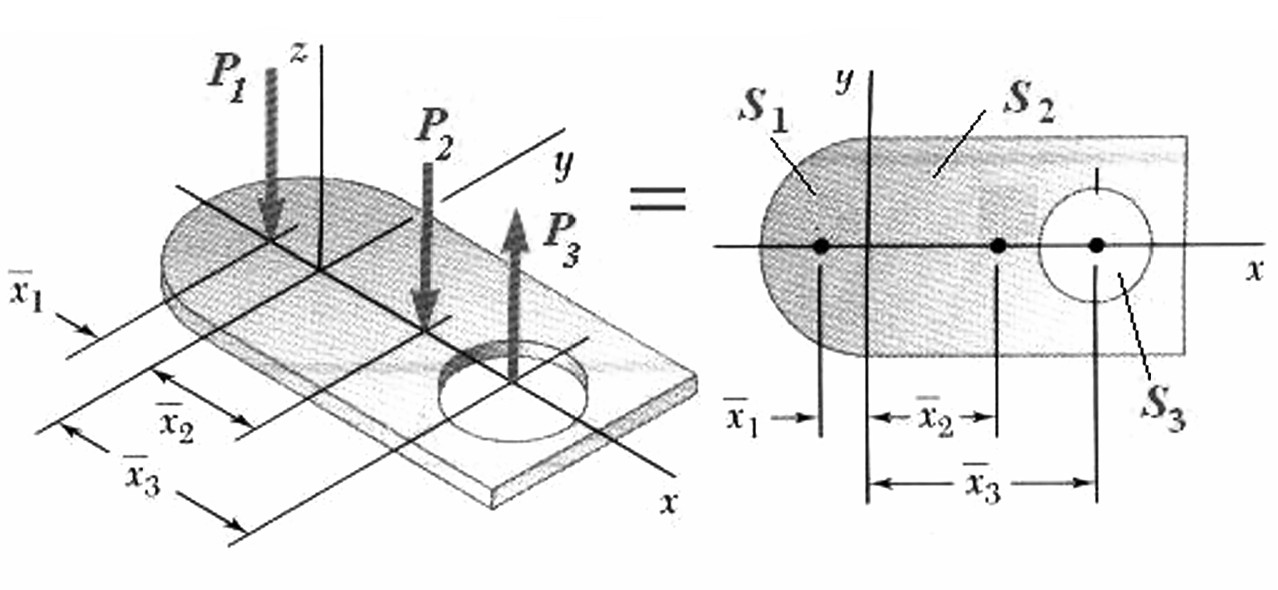
Рис. 5.3

Алгебраическая величина площади частей, из которых составлена вся область пластины (рис. 5.3), знак минус принимается для вырезов (выемок).

◄

◄

	Составляющие пластины
1	прямоугольник	128=96	6	4	576	384
2	треугольник	0.5126=36	4	2	144	72
3	полукруг	0.562 =56.55	6	10,55	339.3	596.4
4	полый круг	42 = 50.27	6	8	301.6	402.2
	Итого	=138.28			=757,7	=506,2

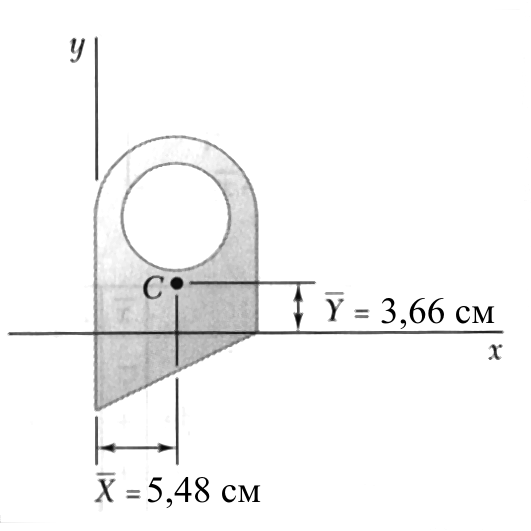
Рис.5.4

Пример 5.2. Определение центра тяжести однородного стержня (провода) (рис.5.5)

	Элементы отрезков
1	AB	60	30	0	18102	0
2	BC	65	30	125	19.5102	8.13102
3	CA	25	0	125	0	3.13102
	Итого	=150			=37.5102	=11.26102

◄

◄

Рис.5.5

Пример 5.3. Определение центра тяжести однородного объемного тела (рис 5.6)

	Элементы объемного тела	Объем,
1	полусфера		2.25	10.16102
2	цилиндр		5	56.55102
3	конус		7.5	 28.28102
	Итого	12.06102		=18.09102

◄

Рис. 5.6

М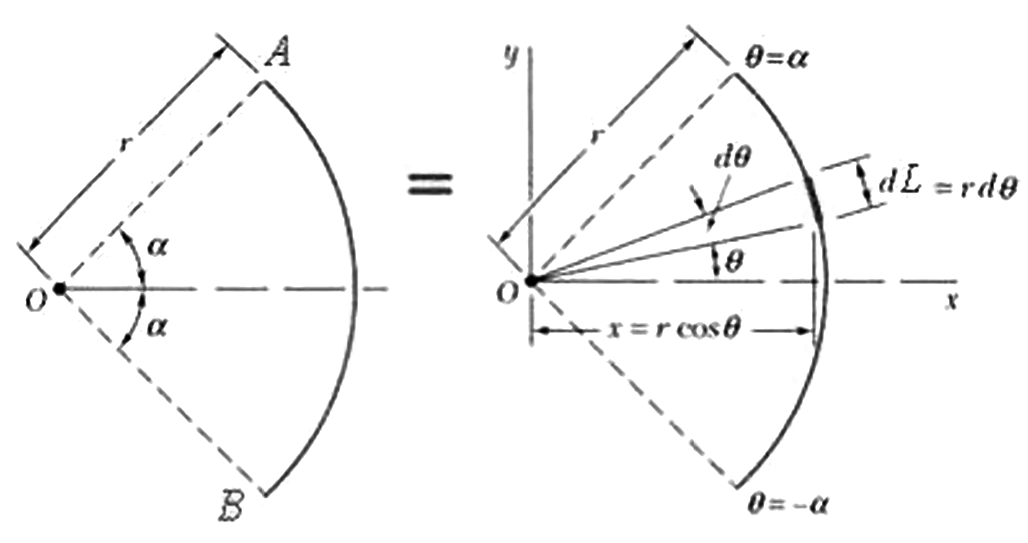 етод симметрии. Центр тяжести симметричных тел. Если однородное тело имеет плоскость, ось или центр материальной симметрии, то его центр тяжести находится соответственно в плоскости, на оси или в центре симметрии. Например, центр тяжести дуги окружности (рис. 5.7) или однородного тела вращения (рис.5.10, 5.11) лежат на оси симметрии, шара  в его центре и т.п.

Пример 5.4. Центр тяжести дуги окружности (рис.5.7) радиусом r c центральным углом 2. Центр тяжести лежит на оси симметрии Ox. Для определения абсциссы выделим элемент дуги длиной . Длина дуги окружности определяется как

Рис. 5.7

Так как , где = ,

◄

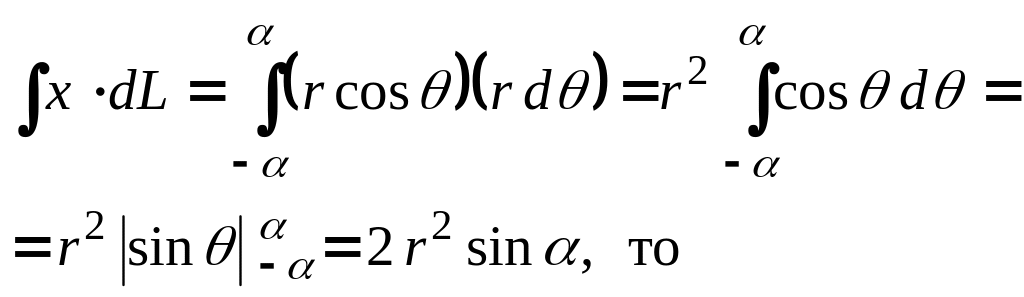
Для дуги полуокружности имеем Так как < , то

ц ентр тяжести лежит внутри сектора АОВ (рис.5.7).

Рис. 5.8

Теоремы Паппа  Гюльдена, позволяют определить положение центра тяжести линии и плоской фигуры в тех случаях, когда известны поверхность или объем тела, образованных вращением линии или фигуры вокруг оси, лежащей в их плоскости.

Теорема 1. Площадь поверхности, образованной вращением плоской кривой вокруг оси, лежащей в плоскости кривой и ее не пересекающей, равна произведению длины этой линии на длину окружности, описываемой ее центром тяжести (рис. 5.8 и рис. 5.10).

Т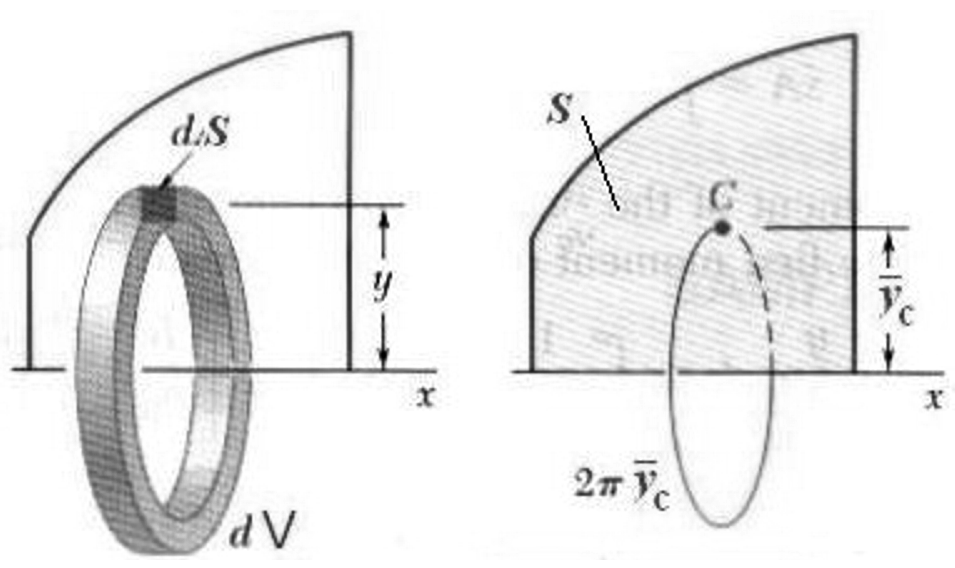 еорема 2. Объем тела, образованного вращением плоской фигуры вокруг оси, расположенной в плоскости фигуры и ее не пересекающей, равен произведению площади фигуры на длину окружности, описываемой ее центром тяжести (рис.5.9).

Рис.5.9

Пример 5.5. Определение положения центра тяжести линии в том случае, когда известна поверхность, образованная вращением линии или фигуры вокруг оси, лежащей в их плоскости (рис. 5.10).

Согласно теоремы 1 Паппа  Гюльдена , с учетом величины абсциссы

четверти окружности взятой из табл. 5.1, и равной , находим абсциссу центра тяжести этой линии относительно вертикальной оси вращения длину четверти окружности и

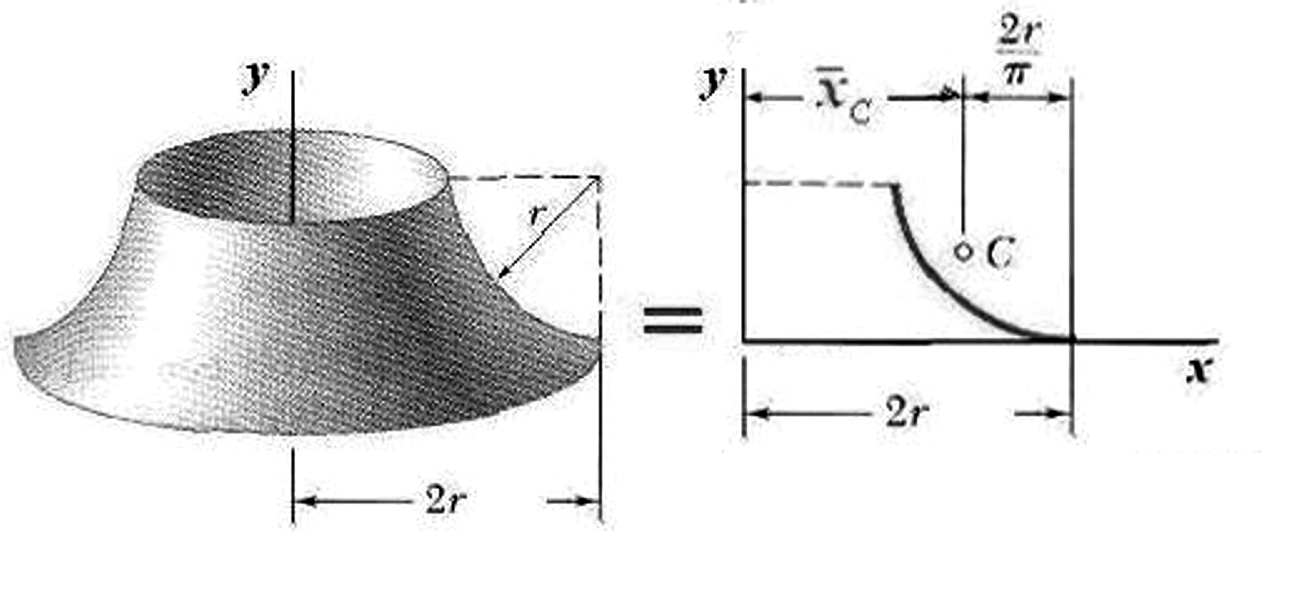
Рис. 5.10

площадь поверхности ее вращения, вокруг вертикальной оси y:

◄

Метод интегрирования. Когда тело нельзя разбить на составные части, центр тяжести которых известен, используют метод интегрирования, являющийся универсальным.

Пример 5.6. Определить центр тяжести полуэллипсоида вращения (рис.5.11).

Так как полуэллипсоид вращения симметричен относительно оси x, а плоскость xy  плоскость симметрии тела вращения, то

В сечении полуэллипсоида вращения плоскостью, параллельной плоскости yOz и отстоящей на расстоянии x от нее, получится круг

. Его площадь , поэтому объем полуэллипсоида

Так как ось Ox ось симметрии полуэллипсоида, то его центр тяжести лежит на оси Ox, а координата центра тяжести определяется прямым интегрированием по x и dx по формуле

 ◄

Рис. 5.11

Т а б л и ц а 5.1

Центры тяжести простейших тел (тонких однородных пластин и линий)

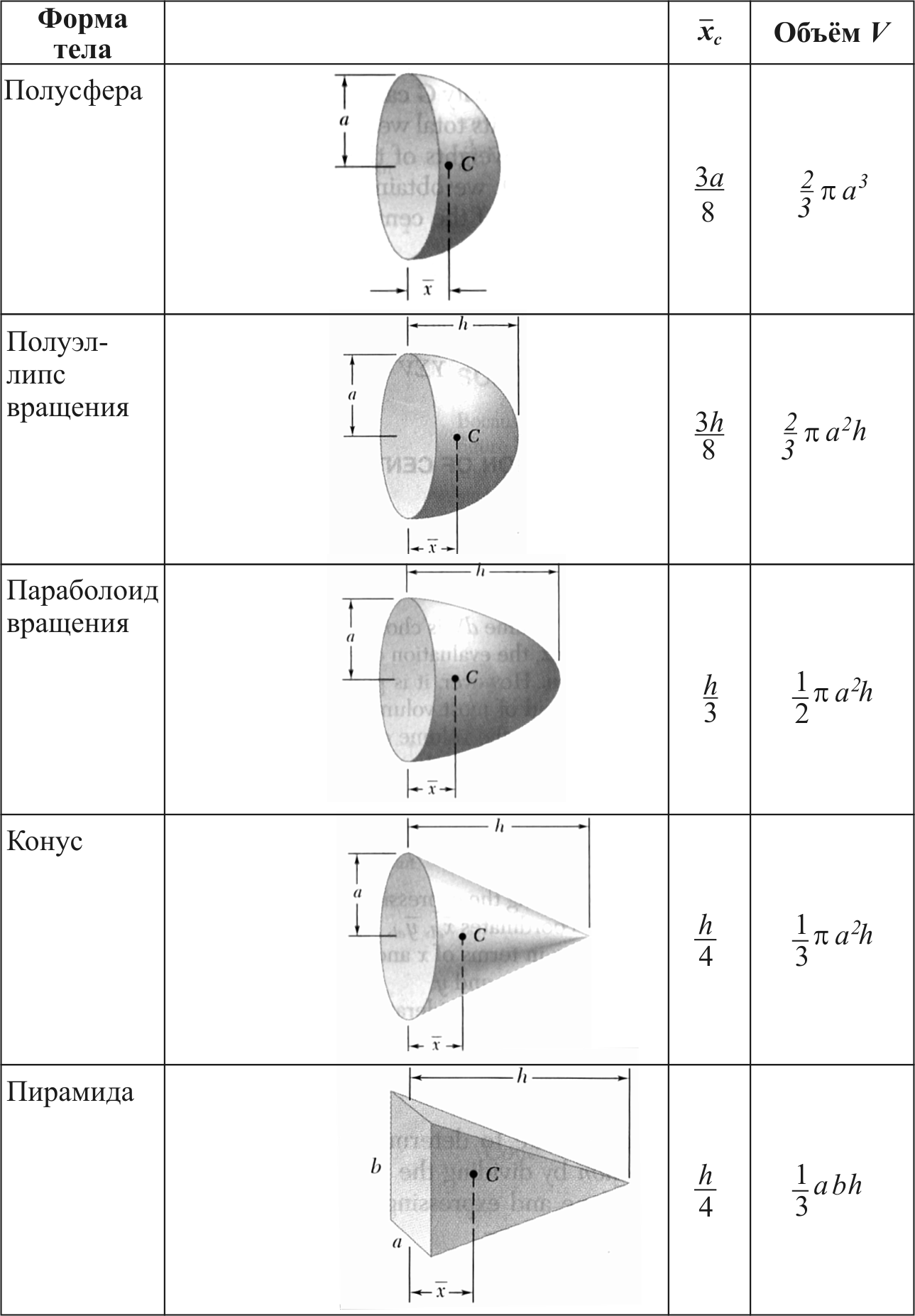
Т а б л и ц а 5.2.

Центры тяжести простейших однородных объемных тел

РАСЧЕТНАЯ РАБОТА №5.