5. Окружность полюсов

Анализ зависимостей, связывающих маневрирование кораблей с полюсом маневрирования, показывает, что при прямолинейном равномерном движении двух кораблей место полюса маневрирования остается постоянным только до тех пор, пока курсы или скорости кораблей достаются неизменными. При изменении параметров движения одного из кораблей место полюса смещается.

Рассмотрим закономерности изменения положения полюса маневрирования при изменении скорости и курса маневрирующим кораблем.

5.1. При изменении курса.

Пусть отношение скоростей m = const, а  изменяется в пределах от 0 до ± 180º. Выражение (1.9) в этом случае будет иметь вид:

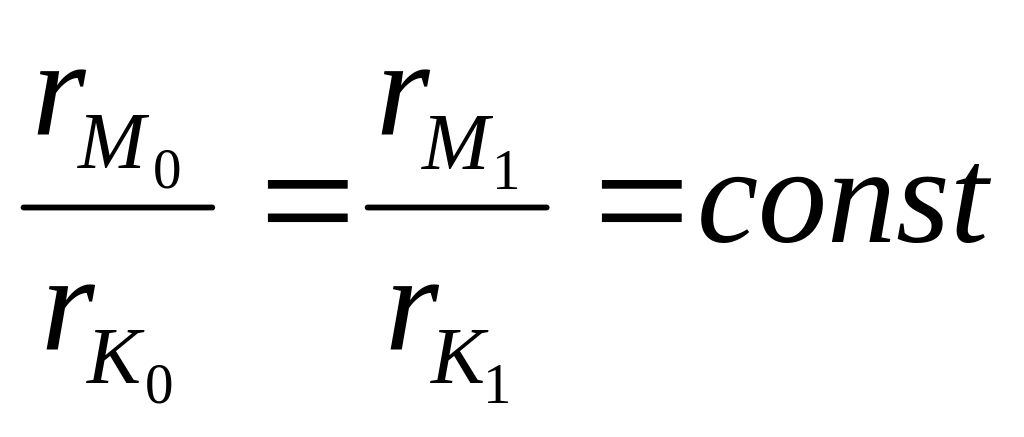
Но, в работе Аполлония (III в. до н.э.) о конических сечениях было установлено, что [Мод] уравнением линии, отношение расстояний каждой точки которой до двух данных различных точек равно одному и тому же числу, для всех точек линии, является уравнение окружности.

Окружность, определяемую таким свойством, называют иногда окружностью Аполлония. Тогда, принимая во внимание (2.8), определим параметры этой окружности:

1

5.1)

. При  = 0º α_м = 0 r_м =

2

5.2)

. При  = 180º α_м = 0 или 180º r_м =

При значениях  полюса маневрирования расположены на окружности симметричной относительно линии пеленга.

Центр окружности находится на продолжении линии пеленга и смещен относительно позиции тихоходного корабля в противоположную от быстроходного корабля сторону.

Радиус окружности зависит от соотношения скоростей и расстояния между кораблями. При m = 1 окружность превращается в прямую линию перпендикулярную линии пеленга.

Действительно, обозначая С = D/V_ с учетом (1.12) получим:

r_М =СV_М r_К =СV_К

т огда, поместив в позицию М₀ начало декартовой системы координат и направив ось X по пеленгу на цель, (Рис.8.)можно написать:

Разделив первое выражение на второе, получим:

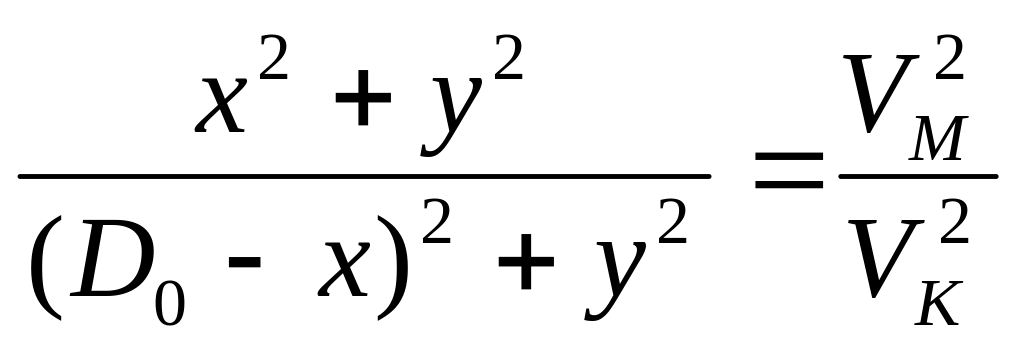
т.к. то, освобождаясь от знаменателя и приводя подобные члены, будем иметь:

5.3)

Выражение (4.3) представляет собой уравнение окружности в декартовых координатах. Найдем точки пересечения этой окружности с линией пеленга. Поскольку в этом случае y = 0, то (4.3) примет вид:

5.4)

Следовательно:

5.5)

тогда радиус окружности:

5.6)

А центр окружности будет смещен от начала координат (позиции тихоходного корабля) на величину:

5.7)

Знак () в выражении (4.7) показывает, что смещение происходит в направлении противоположном пеленгу на объект маневра.

График изменения радиуса окружности полюсов R и смещения центра окружности S_Ц в зависимости от величины m приведен на рис. 9.

Семейство окружностей полюсов для различных значений m, полученных при изменении  [, 180] изображено на рис. 10

Рис.9