Глава 2 Решение систем линейных уравнений

Наиболее компактная форма записи для систем линейных алгебраических уравнений:

Ax=B, где (2.1)

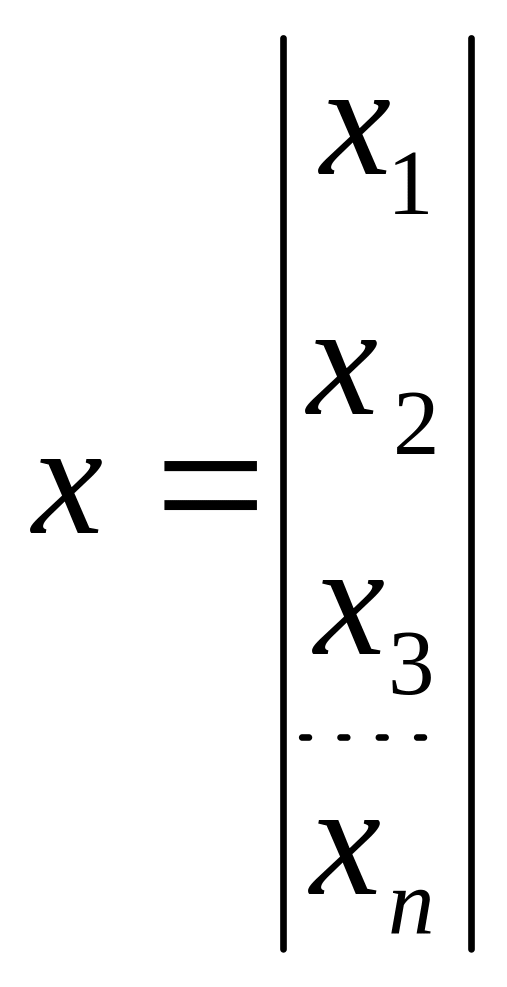, A и B – матрицы, состоящие из вещественных чисел.

Система уравнений может иметь:

- единственное решение;

- бесконечное множество решений;

- не иметь решения.

Система называется вырожденной, если она не имеет решения или их бесконечное множество.

Существуют плохо обусловленные системы, когда можно получить недостоверное решение. Ранее приведен пример такой системы (1.5).

Для системы двух уравнений легко показать физический смысл решения графически.

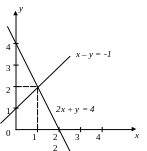
рис. 2.1

Отсутствие решений – это две параллельные прямые, бесконечное множество решений – это совпадение прямых.

При этом в матрице A обнаружится линейная зависимость строк или столбцов.

В пространстве трех переменных получим точку пересечения трех плоскостей, если решение существует. Случаи отсутствия решений или множества решений также вполне понятны. На отсутствие решений указывает также равенство определителя матрицы A нулю. Если ввести матрицу A, то определитель можно рассчитать так: det(A). Очень малое значение определителя не означает, что при поиске решения системы возникнут трудности.

Существуют прямые и итерационные методы численного решения систем линейных уравнений. Прямые методы содержат лишь ошибки округления, а итерационные и ошибки ограничения. Но при итерационных методах ошибки округления не накапливаются. При практических расчетах решающими будут иные соображения.

2.1. Метод Гаусса.

Рассмотрим его на примере системы трех уравнений:

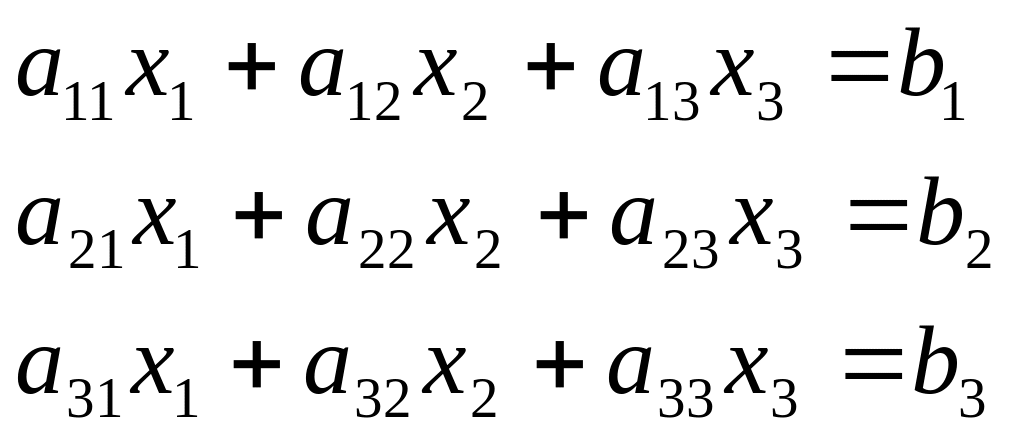, где (2.2)

поэтому .

Метод Гаусса содержит два этапа:

На первом этапе матрица А приводится к верхней треугольной форме, а на втором этапе, полученная система решается обратной подстановкой.

1 этап.

Водим множитель и умножаем на него первое уравнение. Затем вычитаем из второго уравнения полученное первое: .

Так как , второе уравнение приобретает вид Новые обозначения понятны.

Введем множитель . Вновь умножим на него первое уравнение и вычтем его из третьего:

.

Вновь и получили третье уравнение системы:

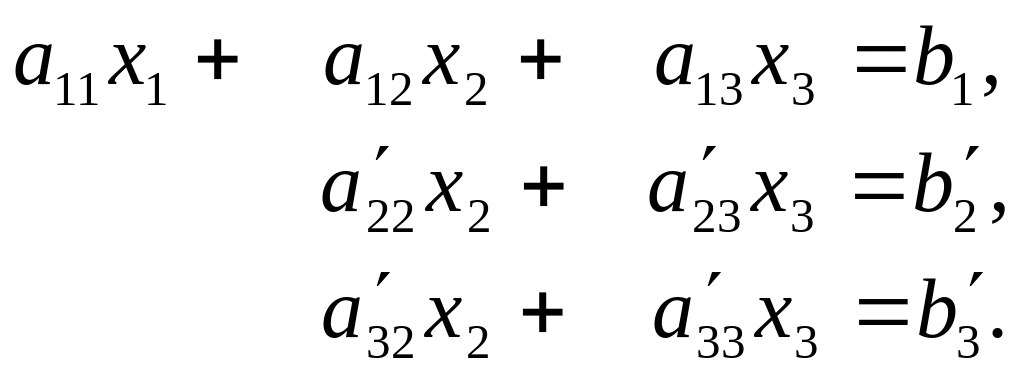(2.3)

Вводим новый множитель . Умножаем на него второе уравнение системы (2.3) и вычитаем его из третьего уравнения:

.

Получили систему уравнений в виде:

(2.4)

Матрица А приобрела верхнюю треугольную форму:

.

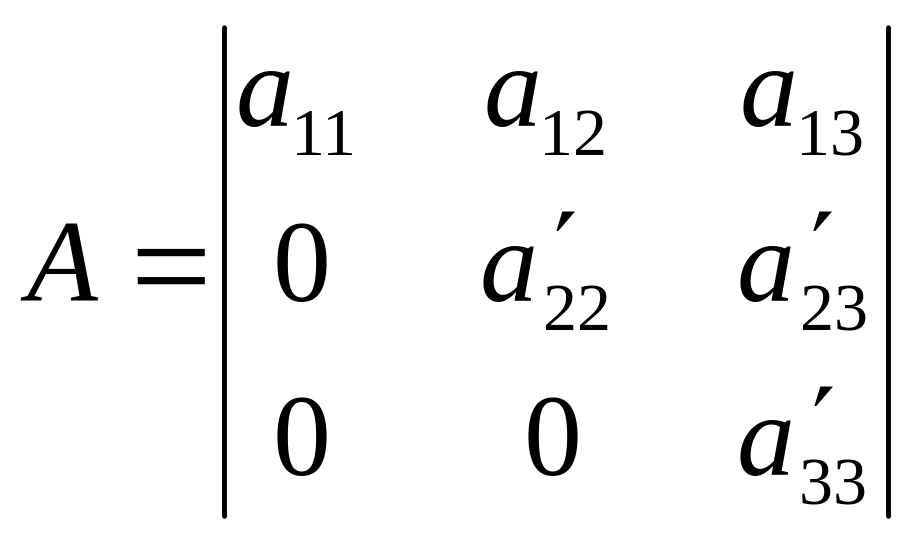2 этап.

Теперь легко выполнить второй этап метода Гаусса – обратную подстановку: Ясно, что реализовать алгоритм метода Гаусса можно лишь в том случае, если

В противном случае система является вырожденной.

В общем виде решение системы уравнений обратной подстановкой можно записать так:

i – строка,

j - столбец,

n – число уравнений.

Доказано, что накопление ошибок округления можно уменьшить, если оперировать с множителями Гауссова исключения m_i<1. Для этого требуется переставлять строки матрицы A так, чтобы диагональный элемент был максимально возможным. Это усложняет алгоритм, но уменьшает ошибки округления. Существуют алгоритмы, позволяющие переставлять не только строки, но и столбцы при выборе наибольшего диагонального элемента. В этом случае приходится переименовывать переменные. Такое усложнение алгоритма не всегда оправдано, так как существенно понижает его эффективность.

Рассмотрим алгоритм Гаусса на примере системы:

10x₁-7x₂=7

-3x₁+2x₂+6x₃=4

5x₁-x₂+5x₃=6

Запишем в векторно-матричной форме

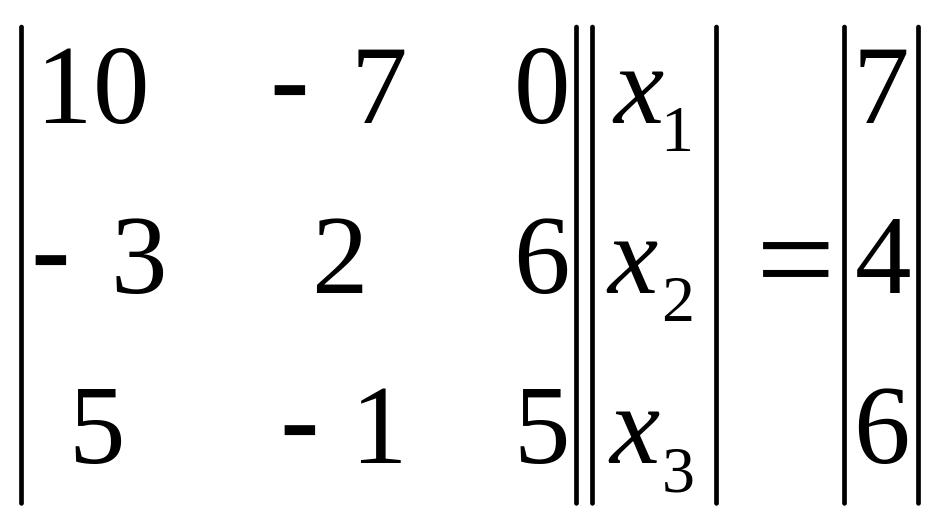, т.е. Ax=b.

Рассмотрим последовательные шаги превращения матрицы А в верхнюю треугольную форму.

Прямой ход

1)Умножаем первое уравнение на коэффициент m=а₂₁/а₁₁=3/10=0,3 и складываем со вторым уравнением

3х₁ – 2,1х₂ = 2,1

-3х₁ + 2х₂ + 6х₃ = 4

0 – 0,1х₂ +6х₃ = 6,1

получим матрицу 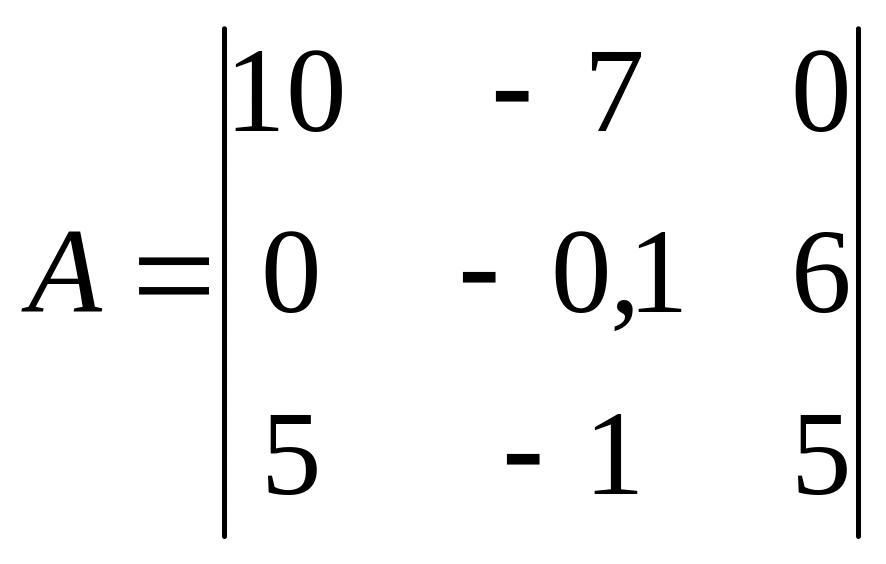и

2) Умножаем первое уравнение на коэффициент m=а₃₁/а₁₁= - 5/10=-0,5 и складываем с третьим уравнением:

-5х₁ + 3,5х₂ = -3,5

5х₁ - х₂ + 5х₃ = 6

0 + 2,5х₂ +5х₃ = 2,5

матрицы ; ;

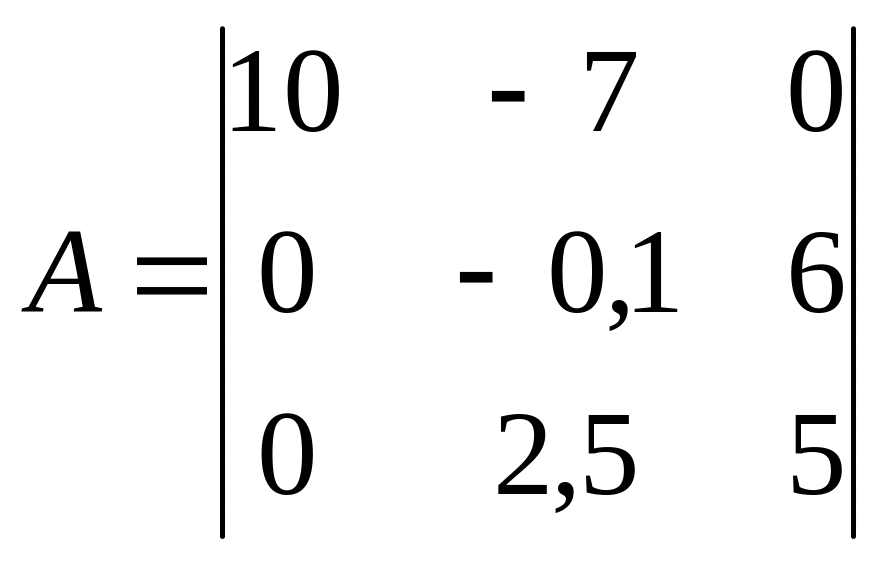3) В данном примере можно на следующем шаге алгоритма поступить, как и ранее, но мы сделаем следующее:

Переставим строки 2 и 3 матрицы А и b местами. Это позволит избежать в общих случаях ошибок округления. Получим матрицы А и b в виде:

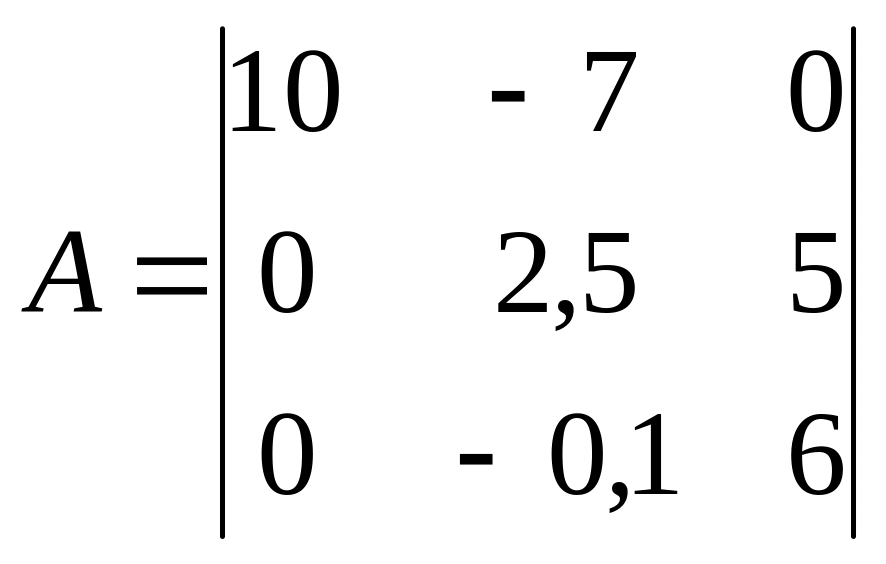
4) Умножим второе уравнение на коэффициент m=а₃₂/а₂₂=+0,04 и сложим с третьим уравнением:

0 + 0,1х₂ + 0,2х₃ = 0,1

0 – 0,1х₂ + 6х₃ = 6,1

0 + 0 +6,2х₃ = 6,2

Получаем матрицы А и b в виде:

, .

В третьем уравнении осталась неизвестная х₃, которая х₃=6,2/6,2=1.

Обратный ход

Т.е. мы приступили ко второму этапу метода – к обратной подстановке (обратному ходу). Точно также из второго уравнения получим и из первого уравнения . В общем случае обратный ход можно выполнить по формулам:

.

Метод Гаусса пережил ряд метаморфоз. В 40-х годах работы Д.Неймана подчеркнули наиболее пессимистические особенности метода и он утратил популярность. В 60-х годах благодаря работам Д.Уилкинсона метод вновь занял достойное положение в численном анализе. Современные исследования подтверждают качественную работу алгоритма Гаусса, если система не вырожденна.

Наиболее достоверной оценкой вырожденности матрицы является число обусловленности cond. Если cond(A) велико (несколько порядков), то матрица близка к вырожденной. Малость числа обусловленности не является препятствием для получения решения.

Приведем программу, реализующую метод Гаусса с выбором главного элемента:

function [X]=gauss(A,B)

%Вводятся матрицы A=[1 2 1 4;2 0 4 3;4 2 2 1;-3 1 3 2];

% и B=[13 28 20 6]';

%Выход - вектор X - решение системы

%Обращение [X]=gauss(A,B)

[N N]=size(A);

X=zeros(N,1);

C=zeros(1,N+1);

%Расширенная матрица AuB

AuB=[A B];

for p=1:N-1

%Выбор главного элемента для столбца p

[Y,j]=max(abs(AuB(p:N,p)));

%Меняем местами строки p и j

C=AuB(p,:);

AuB(p,:)=AuB(j+p-1,:);

AuB(j+p-1,:)=C;

if AuB(p,p)==0 'A вырождена'

break

end

%Процесс исключения для столбца p

for k=p+1:N

m=AuB(k,p)/AuB(p,p);

AuB(k,p:N+1)=AuB(k,p:N+1)-m*AuB(p,p:N+1);

end

end

%Обратная подстановка

X=obrpodst(AuB(1:N,1:N),AuB(1:N,N+1));

Программа метода обратной подстановки.

function X=obrpodst(A,B)

%Верхняя треугольная матрица А

%Матрица превой части В

%Решение X

n=length(B);

X=zeros(n,1);

X(n)=B(n)/A(n,n);

for k=n-1:-1:1

X(k)=(B(k)-A(k,k+1:n)*X(k+1:n))/A(k,k);

end