2. Авторегрессия первого порядка. Тест Дарбина-Уотсона

Как правило, если автокорреляция присутствует, то наибольшее влияние на последующее наблюдение оказывает результат предыдущего наблюдения. Наличие автокорреляции между соседними членами позволяет определить тест Дарбина-Уотсона, который основан на простой идее: если корреляция ошибок регрессии не равна нулю, то она присутствует и в остатках регрессии

, получающихся в результате применения обычного метода наименьших квадратов. В тесте Дарбина-Уотсона для оценки корреляции используется статистика вида

.

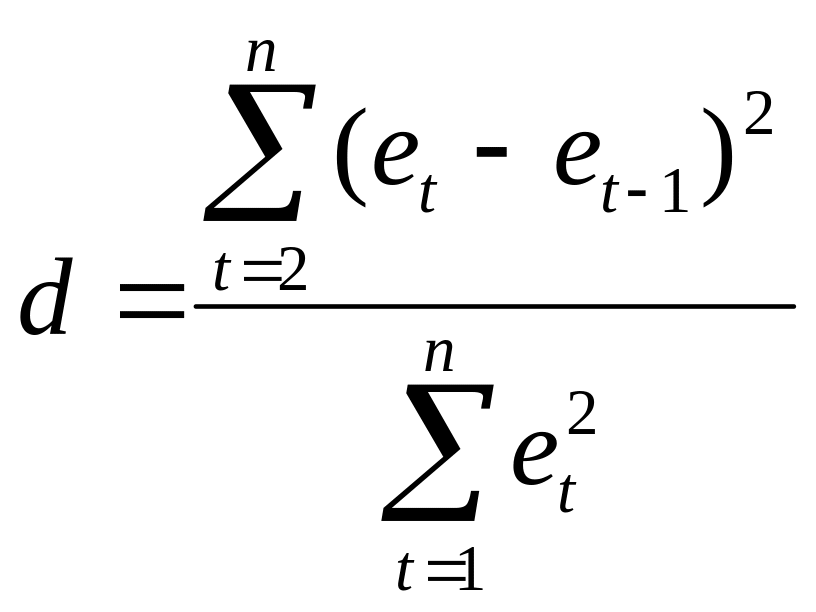Несложные вычисления позволяют проверить, что статистика Дарбина-Уотсона связана с выборочным коэффициентом корреляции следующим образом: . В случае отсутствия автокорреляции выборочный коэффициент r окажется не сильно отличающимся от нуля, а значение статистики d будет близко к двум.

Общая схема критерия Дарбина-Уотсона следующая:

1. По построенному эмпирическому уравнению регрессии

определяются значения отклонений для каждого наблюдения .

2. По формуле рассчитывается статистика Дарбина-Уотсона.

3. По таблице критических точек Дарбина-Уотсона определяются два числа и 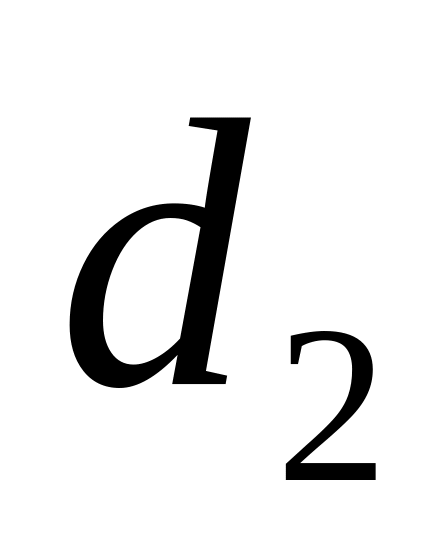, зависящие только от числа наблюдений, числа регрессоров и уровня значимости. Выводы осуществляются по правилу:

– существует положительная автокорреляция,

– вывод о наличии автокорреляции не определен,

– автокорреляция отсутствует,

– вывод о наличии автокорреляции не определен,

– существует отрицательная автокорреляция.

Изобразим результат Дарбина-Уотсона графически:

Отметим, что при использовании критерия Дарбина-Уотсона необходимо учитывать следующие ограничения.

1. Критерий d применяется лишь для тех моделей, которые содержат свободный член.

2. Предполагается, что случайные отклонения определяются по итерационной схеме: 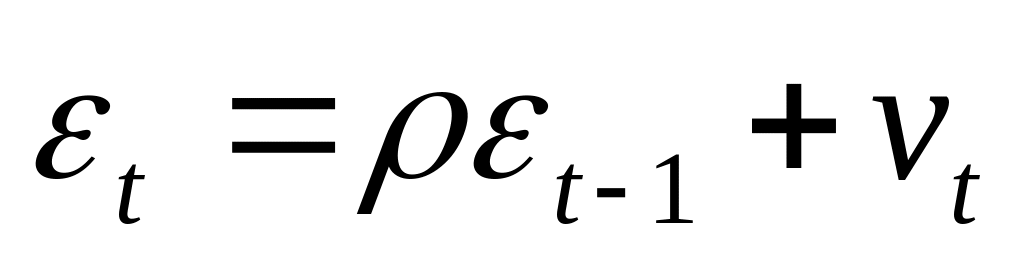, называемой авторегрессионной схемой первого порядка . Здесь - случайный член.

3. Статистические данные должны иметь одинаковую периодичность (т.е. не должно быть пропусков в наблюдениях).

4. Критерий Дарбина-Уотсона не применим для регрессионных моделей, содержащих в составе объясняющих переменных зависимую переменную с временным лагом в один период, т.е. для так называемых авторегрессионных моделей вида:

.

4. Аналитическое выравнивание (сглаживание) временного ряда

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции (тренда, либо тренда с циклической или (и) сезонной компонентой) , характеризующей зависимость уровней ряда от времени. Этот способ называют аналитическим выравниванием временного ряда.

Для решения этой задачи вначале необходимо выбрать вид функции . Наиболее часто используются следующие функции:

• линейная -

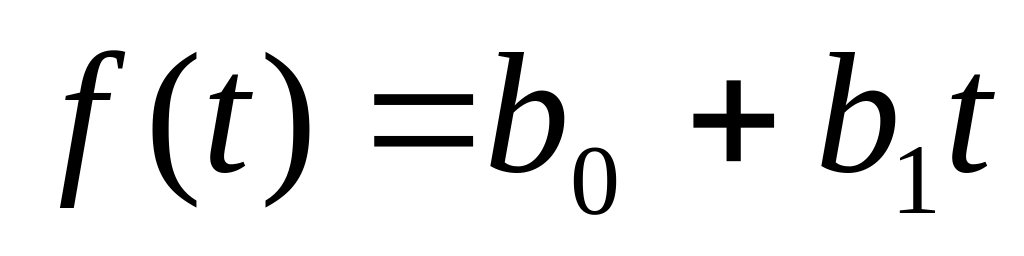
• полиномиальная -

• экспоненциальная -

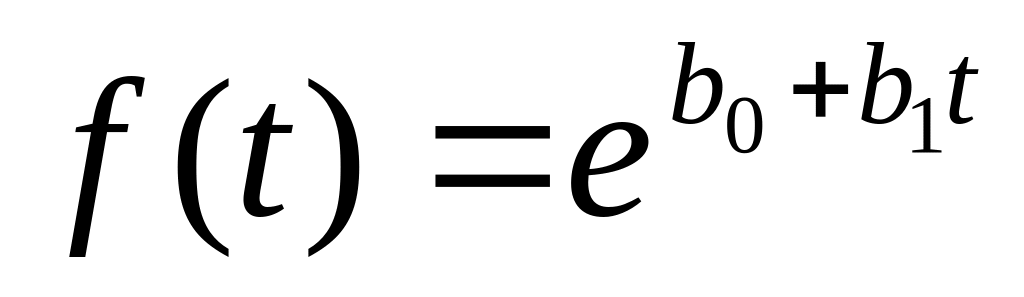
• логистическая -

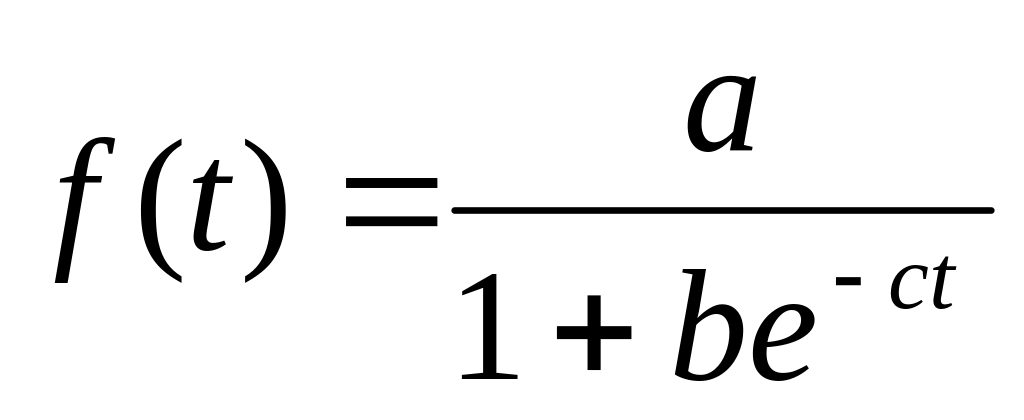
• Гомперца -

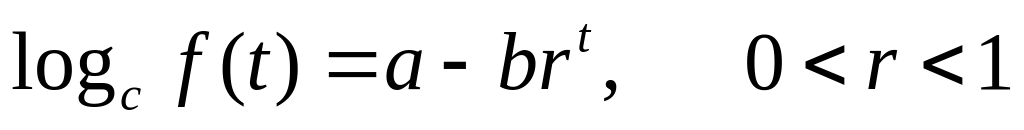
Это весьма ответственный этап исследования. При выборе соответствующей функции используют содержательный анализ (который может установить характер динамики процесса), визуальные наблюдения (на основе графического изображения временного ряда). При выборе полиномиальной функции может быть применен метод последовательных разностей (состоящий в вычислении разностей первого порядка , второго порядка и т.д.), и порядок разностей, при котором они будут примерно одинаковыми, принимается за степень полинома.

Из двух функций предпочтение обычно отдается той, при которой меньше сумма квадратов отклонений фактических данных от расчетных на основе этих функций. Но этот принцип нельзя доводить до абсурда: так, для любого ряда из точек можно подобрать полином -ой степени, проходящей через все точки, и соответственно с минимальной – нулевой – суммой квадратов отклонений, но в этом случае, очевидно, не следует говорить о выделении основной тенденции, учитывая случайный характер этих точек. Поэтому при прочих равных условиях предпочтение следует отдавать более простым функциям.

Параметры основной тенденции можно определить, используя метод наименьших квадратов. При этом, значения временного ряда рассматриваются как зависимая переменная, а время - как объясняющая:

(7.9)

где – возмущения, удовлетворяющие основным предпосылкам регрессионного анализа, т.е. представляющие независимые и одинаково распределенные случайные величины, распределение которых предполагаем нормальным.

Согласно методу наименьших квадратов параметры прямой находятся из системы нормальных уравнений (2.5), в которой в качестве берем :

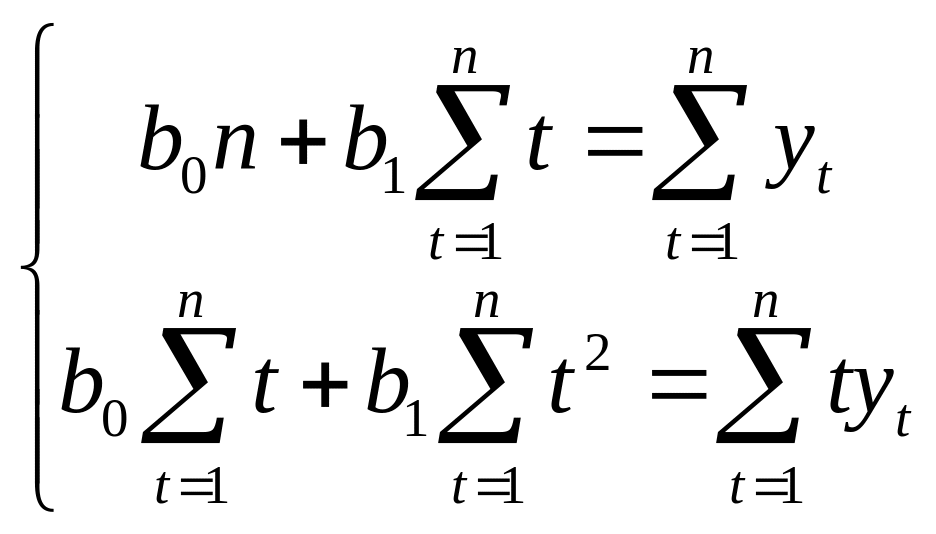(7.10)

Учитывая, что значения переменной образуют натуральный ряд чисел от 1 до , суммы можно выразить через число членов ряда по известным в математике формулам:

(7.11)

В рассмотренном примере 2 на странице 79 система нормальных уравнений имеет вид:

,

откуда и уравнение тренда , т.е. спрос ежегодно увеличивается в среднем на 25,7 ед.

Проверим значимость полученного уравнения тренда по F-критерию на 5%-ном уровне значимости вычислим с помощью формулы (3.40) суммы квадратов:

а) обусловленную регрессией –

б) общую –

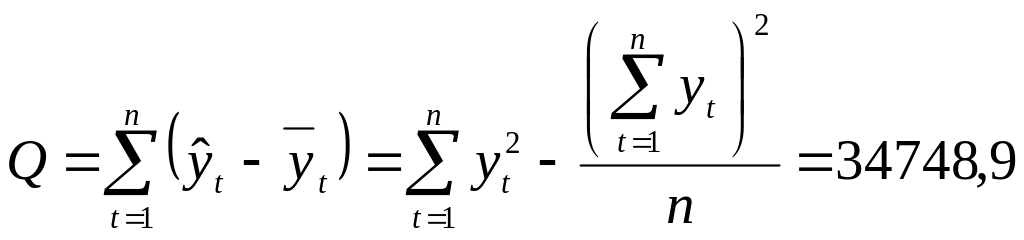
в) остаточную

.

Найдем значение статистики:

.

Так как , то уравнение тренда значимо.

Другим методом выравнивания (сглаживания) временного ряда, т.е. выделения неслучайной составляющей, является метод скользящих средних. Он основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени «скользит» вдоль ряда.

Получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд, из-за усреднения отклонений ряда.