§ 2. Инварианты левой части общего уравнения линии второго порядка относительно преобразования поворота.

Пусть дано общее уравнение линии второго порядка:

. (10)

Найдем инварианты левой части уравнения (10) относительно преобразования системы координат. Преобразование поворота системы координат имеет вид:

(11)

При этом преобразовании общее уравнение второй степени (10) преобразуется в уравнение

,

причем три старших члена уравнения (10) преобразуются в старшие члены уравнения , то есть

, (12)

а из формул преобразования (11) видно, что

Из (12) и следует, что при любом значении справедливо равенство

,

или

. (13)

В левой части равенства (13) имеется квадратичная форма переменных x,y, а в правой части – квадратичная форма, полученная из нее линейным преобразованием (11), причем равенство (13) справедливо при любых значениях . По теореме о линейном преобразовании переменных квадратичной формы имеем:

.

Так как определитель преобразования

то

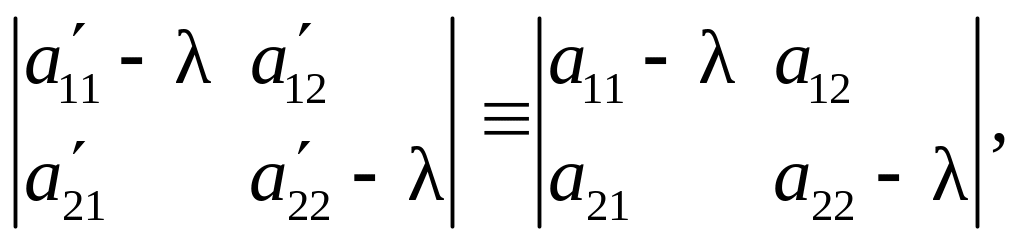
или

.

Из этого соотношения получаем:

,

.

Из определения инвариантов следует, что и являются инвариантами левой части уравнения (10) относительно преобразования поворота системы координат вокруг начала координат.

Для того, чтобы найти остальные независимые инварианты уравнения (10), рассмотрим квадратичную форму Ф трех переменных x, y, t:

, (14)

причем ее коэффициенты и соответствующие коэффициенты левой части общего уравнения (10) одинаковы, то есть

.

Совершим следующее линейное преобразование переменных квадратичной формы:

(15)

Очевидно, что в результате преобразования (15) квадратичная форма (14) преобразуется в квадратичную форму

причем коэффициенты квадратичной формы равны соответствующим коэффициентам левой части преобразованного уравнения .

Итак,

. (*)

Из формул преобразования (15) имеем:

(**)

Если обе части равенства (**) умножить на произвольное число и вычесть из равенства (*), то получим:

Левая часть этого тождества есть симметричная квадратичная форма, а правая часть – квадратичная форма, полученная из нее линейным преобразованием (15) переменных x, y, t. По теореме о линейном преобразовании квадратичной формы при любом значении имеет место равенство:

,

или

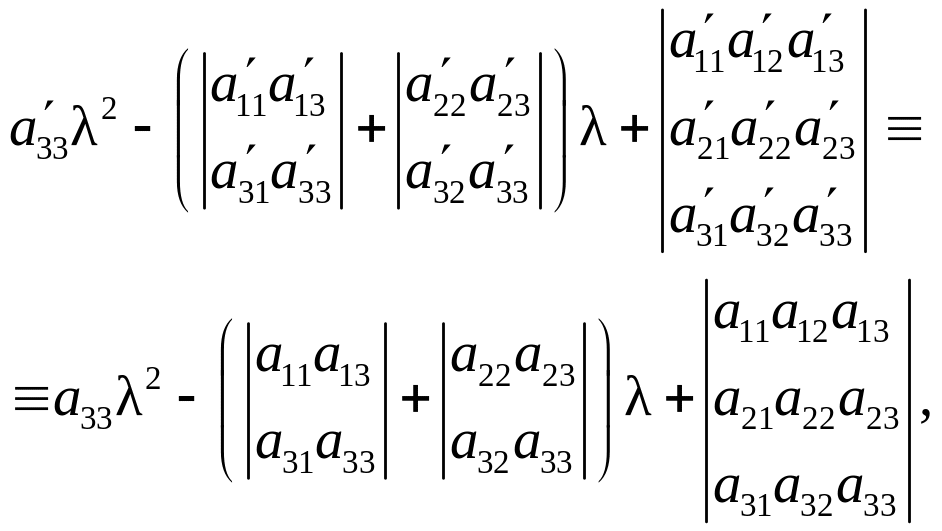
откуда

.

Итак, - инварианты левой части уравнения (10) относительно преобразования поворота.

§3. Определение расположения центральной линии второго порядка.

Если за оси координат принять прямые, проходящие через центр и имеющие главные направления относительно линии второго порядка, то уравнение этой линии относительно новой системы координат в случае будет иметь вид:

Следовательно, для того чтобы построить центральную линию второго порядка, заданную общим уравнением (10) относительно исходной системы координат, нужно:

1. Вычислить инварианты и убедиться в том, что .

2. Найти корни характеристического уравнения

3. Записать приведенное уравнение

И привести его к каноническому виду.

4) Найти уравнения осей:

ось :

ось :

и построить оси по найденным уравнениям.

За положительное направление оси можно принять любое из двух возможных, но тогда за положительное направление оси нужно принять то направление, с которым совпадает положительное направление оси при повороте ее вокруг точки против вращения часовой стрелки на угол .

5) Построить данную линию относительно системы координат по каноническому уравнению.

Пример 1. Построить линию .

Решение. 1) Вычислим инварианты:

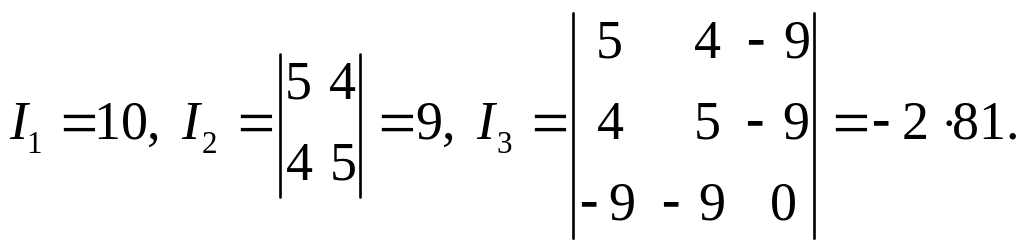
2) Найдем корни характеристического уравнения:

, , .

3) Так как , то приведенное уравнение имеет вид:

или каноническое уравнение

есть уравнение эллипса.

4) Найдем уравнения осей и построим их:

, ;

или

или

5) Построим эллипс в системе (рис. 5).

Рис. 5

Пример 2. Построить линию:

Решение.

1) Найдем инварианты:

2) Найдем корни характеристического уравнения

.

3) Так как , то приведенное уравнение имеет вид:

или

а это есть каноническое уравнение гиперболы.

4) Найдем уравнения осей и построим их.

следовательно,

ось : или

ось : или

5) Построим гиперболу по каноническому уравнению (рис. 6).

Рис. 6