10. Однородные и линейные дифференциальные уравнения Линейные дифференциальные уравнения

   Уравнение вида y' + P(x) y = Q(x), левая часть которого есть линейная функция относительно y и y' , а функции P(x) и Q(x) непрерывны в некоторой области, называется линейным дифференциальным уравнением первого порядка.

   Уравнение вида y' + P(x) y = 0 называется линейным однородным дифференциальным уравнением первого порядка.

   Рассмотрим линейное однородное дифференциальное уравнение y' + P(x) y = 0. Это и уравнение с разделяющимися переменными, значит,

              = – P(x) y

или

              = – P(x) dx.

Проинтегрируем последнее уравнение:

              = –  P(x) dx + C,

            ln y = ln C –  P(x) dx.

Общее решение линейного однородного дифференциального уравнения имеет вид

            y = C .

11. Дифференциальные уравнения в полных дифференциалах

Д.У. P(x;y)dx + Q(x;y)dy=0 (1)

наз-ся уравнением в полных дифференциалах если левая часть этого уравнения

представляет собой полный дифференциал некоторой функции U(x;y)/

Необходимым и достаточным условием, того ,что уравнение (1) будет уравнением

в полных дифференциалах, выполнение равенства

dP/dy=dQ/dx

Действительно, если левая часть равенства (1) есть полный диф. функции U(x;y)

,то dU(x;y)=P(x;y)+Q(x;y)dy

dU(x;y)= dU/dx*dx + dU/dy*dy (3)

dU(x;y)= P(x;y)dx+Q(x;y)dy (4)

Сравнивая рав. 3 и 4

dU/dx=P(x;y) (5)

dU/dy=Q(x;y) (6)

dP/dy=d^2U/dxdy

dQ/dx=d^2U/dydx

Т.к для диф. ф-ции U(x;y) частная произв. 2-го порядка не зависят от порядка

диф., то мы приходим к равенству (2). С учётом равенства(30 равенство (1)

может быть зависимо как

dU(x;y)=0 (7)

U(x;y)=c (8)

Это и есть общее решение нашего д.у.

Для отыскания ф-ции U воспользуемся ф-лой (5)

dU=P(x;y)dx

U= ò(x;y)dx+C=òP(x;y)dx + j(y) (9)

Для отыскания ф-ции j(y) продифференцируем равенство (9) по переменной y

dU/dy=d/dyòp(x;y)dx+j¢(y)

j¢(y)=Q(x;y)- d/dyòp(x;y)dx (10)

Проинтегрировав левую и правую часть рав. (10) мы получим значение ф-ции j(y):

j(y)=ò(Q(x;y)-d/dy*òP(x;y)dx)dy=C (11)

Подставим равенство (11) в (9)

òP(x;y)dx=ò(Q(x;y)-d/dy*òP(x;y)dx)dy +C=C

òP(x;y)dx+ò(Q(x;y)-d/dy*òP(x;y)dx)dy=C (12)

C=C-C получаем общее решение диф. уравнения.

Замечание.

1.) В ф-ле (12) знаки частной производной и дифференциала можно

поменять местами.

2.) Ф-цию U можно было определить из равенства(6)

12. Некоторые типы ДУ высших порядков допускающие понижение порядка

Будем рассматривать следующие три типа ду, допускающих понижение порядка.

 

1. Простейшие ДУ n-го порядка:

(4)

Решаются   - кратным интегрированием.

 

2. Дифференциальные уравнения, не содержащие явно искомую функцию  :   

.

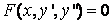(5)

                                                                                             

Метод решения: замена    ;

ДУ (5)  – получилось ДУ I порядка относительно функции  .

 

3. Дифференциальные уравнения, не содержащие явно независимую переменную  :  

(6)

Метод решения: замена    , то есть  ;

тогда   ДУ(6)   - получилось ДУ I порядка, в котором   – это независимая переменная,  – искомая функция.

 

13. Линейные ДУ с постоянными коэффициентами

Уравнение вида 

где a₁, …, a_n – некоторые постоянные, называется линейным дифференциальным уравнением с постоянными коэффициентами.

Всякое решение однородного уравнения первого порядка 

имеет вид 

где C – постоянная.

Уравнение вида 

где P_m (x) – многочлен степени m, μ – постоянная, имеет частное решение вида 

если μ ≠ λ, и вида 

если μ = λ. Здесь Q_m (x) – многочлен степени m.

В общем случае у однородного линейного дифференциального уравнения с постоянными коэффициентами   имеется так называемое характеристическое уравнение   Корни этого уравнения – характеристические числа – являются показателями степеней слагаемых, входящих в решение. Если среди корней уравнения   нет кратных, то решением однородного уравнения является функция вида  где все   – некоторые константы, зависящие от начальных условий. Количество слагаемых в этой функции совпадает со степенью дифференциального уравнения. Если же, скажем,   – корень характеристического уравнения кратности m, то соответствующее слагаемое принимает вид  а общее количество слагаемых, входящих в решение однородного дифференциального уравнения уменьшается на m – 1.