4 Эллиптический параболоид.

Определение 4.1. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид

где  .

Будем считать, что  . Если  , то эллиптический параболоид   --- это параболоид вращения, так как получается вращением параболы

вокруг оси  , являющейся осью этой параболы.

Ось   является осью симметрии эллиптического параболоида  , а плоскости   и   --- его плоскостями симметрии. Начало координат для эллиптического параболоида   является точкой пересечения этой поверхности с ее осью   и называется вершиной.

Рассмотрим сечения эллиптического параболоида   плоскостями  , параллельными плоскости  . Нетрудно видеть, что произвольная такая плоскость пересекает эллиптический параболоид   по линии

или

Если  , то первое уравнение   не имеет действительных решений, так как  . Это означает, что плоскость   при   не пересекает эллиптический параболоид  . Другими словами, эллиптический параболоид   лежит в неотрицательном полупространстве относительно плоскости  . Если  , то первое уравнение   имеет единственное решение  , т.е. плоскость   имеет с эллиптическим параболоидом только одну общую точку   --- вершину. Если   , то, переписав уравнения   в виде

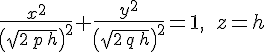
видим, что сечением является эллипс с центром в точке  , оси которого параллельны прямым   и  , а полуоси равны

Заметим, что полуоси увеличиваются по мере удаления плоскости сечения от координатной плоскости  .

Плоскость   пересекает эллиптический параболоид   по параболе

а плоскость   --- по параболе

Таким образом, числа   и   --- параметры парабол  ,  , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями). Рассмотрим теперь сечения эллиптического параболоида   плоскостями, параллельными плоскости  , т.е. плоскостями, выраженными уравнением  . Уравнения линии сечения:

или

или

Эти уравнения выражают параболу с вершиной в точке  , ось, которой выражается уравнениями   и одинаково направленной с осью  . Параметр этой параболы равен  , т.е. параметру главного сечения   эллиптического параболоида.

Таким образом, эллиптический параболоид может быть образован параллельным переносом параболы  , при котором вершина параболы   перемещается по параболе  ; плоскость параболы   перпендикулярна плоскости параболы  , а оси этих парабол параллельны и одинаково направлены.

Аналогичная картина получается и для сечений эллиптического параболоида   плоскостями, параллельными плоскости  .

5 Гиперболический параболоид.

Определение 5.1. Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид

где  .

Для гиперболического параболоида   плоскости   и   являются плоскостями симметрии, а ось   --- осью симметрии. Ось симметрии гиперболического параболоида называется просто его осью. Точка, в которой ось гиперболического параболоида пересекает эту поверхность, называется вершиной. Гиперболический параболоид   имеет вершину в начале координат.

Плоскости   и  , являющиеся для гиперболического параболоида   плоскостями симметрии, называются главными плоскостями гиперболического параболоида.

Гиперболический параболоид

в случае   имеет только одну ось симметрии (ось   ), если же  , то параболоид имеет еще две оси симметрии:

В самом деле, если координаты точки   удовлетворяют уравнению

то этому же уравнению удовлетворяют координаты точки  , симметричной с точкой   относительно прямой  . Так же доказывается, что прямая   является осью симметрии.

Плоскость   пересекает гиперболический параболоид   по линии, определяемой уравнениями

или

которая является совокупностью двух прямых линий:

и

Плоскость  , параллельная плоскости  , пересекает гиперболический параболоид   по линии, определяемой уравнениями:

Если  , то эти уравнения можно переписать в виде

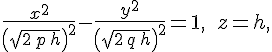
которые определяют гиперболу, расположенную в плоскости   с центром в точке  , действительная ось которой параллельна оси  , а мнимая --- параллельна оси  . Если  , то уравнения   линии сечения можно представить в виде

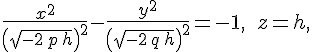
которые определяют гиперболу, расположенную в плоскости   с центром в точке  , действительная ось которой параллельна оси  , а мнимая --- параллельна оси  . Плоскость   пересекает гиперболический параболоид   по параболе

а плоскость   --- по параболе

Таким образом, числа   и   --- параметры парабол  ,  , получающихся в сечении параболоида его плоскостями симметрии (эти параболы называются главными сечениями). Рассмотрим теперь сечения гиперболического параболоида   плоскостями, параллельными плоскости  , т.е. плоскостями, выраженными уравнением  . Уравнения линии сечения:

или

или

Эти уравнения выражают параболу с вершиной в точке  , ось, которой выражается уравнениями   и противоположно направленной с осью  . Параметр этой параболы равен  , т.е. параметру главного сечения  гиперболического параболоида.

Таким образом, гиперболический параболоид может быть образован параллельным переносом параболы  , при котором вершина параболы   перемещается по параболе  ; плоскость параболы   перпендикулярна плоскости параболы  , а оси этих парабол параллельны и противоположно направлены.

Аналогичная картина получается и для сечений гиперболического параболоида   плоскостями, параллельными плоскости  .

Рассмотренные сечения дают представление о форме гиперболического параболоида