11. Понятие об n-мерном векторе. Векторное пространство.

Вектор – направленный отрезок на плоскости или в пространстве, имеющий определённую длину, у которого одна из точек принята за начало, а другая за конец. Длиной вектора (нормой) или модулем называется число, равное длине отрезка, изображающего вектор ax2+y2(+z2). Если начало и конец вектора совпадают, то такой вектор называется нулевым и обозначается 0. Для каждого а, отличного от 0, существует противоположный -а, который имеет модуль, равный а, коллиниарен с ним, но направлен в другую сторону. Два вектора а ив называются коллинеарными, если они расположены на одной прямой или на параллельных прямых. Два вектора называются равными, если они: 1)имеют равные модули; 2)коллиниарны; 3)направлены в одну сторону.

n-мерный вектор- упорядоченный набор n чисел, где каждое из n чисел- соответствующие координаты вектора. x=(x1,x2,xi,xn) Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее всем сво-вам суммы( коммутативное, ассоциативные), называется векторным пространством. Размерность векторного пространства равна количеству векторов в базисе этого пространства. Совокупность n-мерных векторов, рассматриваемая с определёнными в ней операциями сложения векторов и умножения вектора на число, называется n-мерным координатным пространством. Система n—мерных лин. независимых векторов называется базисом Rn (R2-плоскость,R3-пространство), если каждый вектор этого пространства R разлагается по векторам этой системы. Базисом называется совокупность всех лин. независимых векторов системы пространства. Теорема: если диагональная система является частью n-мерных векторов, то она же является базисом этой системы. Теорема: любой вектор системы векторов единственным образов разлагается по векторам её базиса.

12.Линейная зависимость векторов.

Векторы 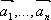называются линейно зависимыми, если существует такая линейная комбинация при не равных нулю одновременно . Если же только при ai = 0 выполняется , то векторы называются линейно независимыми.

1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

6. Любые 4 вектора линейно зависимы.

13. Скалярное произведение векторов, его cв=ва . евклидово пространство.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

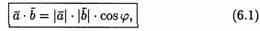
скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства :

1. причем

2. переместительный закон

3. 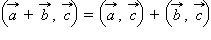распределительный закон

4. сочетательный закон

Векторное пространство, в котором определено скалярное произведение, называется евклидовым пространством.

14. Прямая на плоскости. Ур-е прямой с угловым коэффициентом. Ур-е прямой, проход через данную точку, в заданном направлении. Ур-е прямой, проход через 2 данные точки.

0 ≤α≤π -ур-ие прямой с угловым коэффиц. Подставим в (1); (3)-ур-ие пр., проход. ч/з задан(.) с зад. угловым коэффициентом

;

, подст. в ур (3) : - ур-ие прямой ч/з 2 данные точки.

15. Уравнение прямой в отрезках. Общее уравнение прямой на плоскости.

Вектор n = (А; В) - нормальный вектор прямой.

В векторном виде: n*r + С = 0, где - радиус-вектор произвольной точки на прямой.

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

Уравнение прямой в отрезках

где a, b - величины отрезков, отсекаемых прямой на осях координат.

общее уравнение прямой на плоскости Ах+Ву+С=0:

Ву=-Ах-С (А,В,С не равно 0)

У=(-А/В)*х-С/В

k= -А/В=tgα

Общее уравнение плоскости.

Ax+By+Сz-Ax0-By0-Сz0=0

-Ax0-By0-Сz0=D, где D=Ax+By+Сz

Ax+By+Сz+D=0

16.Углом между двумя прямыми называется любой из двух углов, образованных прямыми при их пересечении.

θ=α₂- α₁

tgθ=tg(α₂-α₁)= (tgα₂ – tgα₁)/(1+ tgα₂*tgα₁)= (k₂-k₁)/(1+k₂*k₁)

tgθ=(k₂-k₁)/(1+k₂*k₁) – формула для вычисления угла между двумя пересекающимися прямыми

1. пусть θ=0, тогда прямые параллельны, tgθ=0 след-но k₁=k₂ – условие параллельности прямых

2. θ=90^о, то tg θ= ∞ или не существует

1+k₁* k₂=0

k₁* k₂= -1 – условие перпендикулярности прямых

17.Расстояние от точки до прямой

Пусть задана прямая Ах+Ву+С=0 и точка М₀(х₀;у₀), не лежащая на прямой. Нужно найти расстояние от точки М₀ до прямой. коллинеарна . ( ; )=А(х₁ – х₀)+В(у₁-у₀). ( ; )= cos = . А(х₁ – х₀)+В(у₁-у₀)= .

d= = 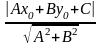------- формула для вычисления расстояния от точки до прямой, С=Ах₁ +Ву₁.

ИЛИ Не из конспекта: d= .

18. Понятие о кривых 2-го порядка. Окружность, эллипс, гипербола, парабола.

Кривые 2го порядка описываются с помощью общего ур-я:

Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где

а) Каноническое ур-е эллипса

- Каноническое ур-е эллипса

Если a=b, то x2+b2=a2 - ур-е окружности.

б) Ур-е гиперболы: x2/a2-y2/b2=1

в) ур-е параболы: y2=2px или y=ax2

г) ур-е сферы: x2+y2+z2=а2 (r2=(x-a)2+(y-b)2+(z-c)2)

д) ур-е эллипса: x2/a2-y2/b2+z2/c2=1

18.Окружность

Это частный случай эллипса. Формула: (х-х₀)²+(у-у₀)²=R², где (х₀;у₀)- координаты центра окружности.

Эллипс, его характеристики, геометрические свойства.

Э.—это геометрическое место точек плоскости, для которых сумма расстояний до двух заданных точек (фокусов) есть величина постоянная (и равна 2а).

. … b²=а²-с²

--каноническое уравнение, где a-большая полуось, b-меньшая полуось.

--- эксцентриситет эллипса. с²=а²-b². .

Прямые называются директрисами Э., параллельны Оу, лежат вне Э.

F₁(-c;0), F₂(c;0) координаты фокусов Э. =1 также каноническое уравнение Э. с центром в т.( х₀;у₀).