44. Теорема о максимальном числе независимых первых интегралов.

Теорема. О максимальном числе независимых первых интегралов.

Максимальное число независимых первых интегралов системы (1) равно её порядку.

Док-во. Пусть независимые первые интегралы системы (1). Существование такого кол-ва первых интегралов доказано ранее. Это означает, что якобиан:

(2)

допустим, что есть ещё один первый интеграл . Записывая необходимое и достаточное условие для первых интегралов получим (n+1) уравнений:

………………………………………(3)

По типу системы (3) составим новую систему для неизвестных :

…………………………(4)

Система (4) представляет собой линейную однородную алгебраическую систему (n+1) для (n+1) неизвестных. Согласно (3) система (4) имеет ненулевое решение: при . Это означает, что определитель системы (4) тождественно равен нулю, т.е. якобиан:

(5)

Соотношение (5) показывает, что межу функциями существует зависимость, и, следовательно, одна из них является функцией остальных. Таким образом, новый первый интеграл есть функция n первых независимых интегралов:

45. Эквивалентность отыскания n независимых первых интегралов построению общего решения нормальной системы.

Теорема. Отыскание n независимых первых интегралов системы (1) равносильно построению общего решения.

Док-во. Покажем, что если известны n первых интегралов, то можно найти частное решение, не проводя никакого интегрирования. Пусть – первые интегралы системы(1). Покажем, что можно найти решение , удовлетворяющие начальным условиям . Вычислим значения первых интегралов в начальной точке :

(2)

составим систему уравнений:

(3)

здесь константы те же самые, что и в (2). Будем в системе (3) считать неизвестными. В силу отличия от нуля якобиана:

систему (3) можно разрешить относительно . Получим:

(4)

Осталось показать, что построенные функции (4) являются решениями системы (1). Поскольку – решения системы (3), то при подстановке должны получатся тождества:

(5)

Полагая в (5) и сравнивая с (2), имеем:

Отсюда,

(6)

Продифференцируем тождества (5) по x:

(7)

Однако, поскольку – первые интегралы, то они должны удовлетворять необходимому и достаточному условию при . Подставляя , имеем:

(8)

Вычитая из уравнений системы (7) одноименные уравнения системы (8), придем к:

(9)

Считая в системе тождеств (9) переменные в квадратных скобках неизвестными, получаем однородную систему уравнений с отличным от нуля определителем. Такая система имеет только тривиальное решение, т.е. справедливы тождества:

Это означает, что функции (4) являются решениями системы , удовлетворяющими заданным начальным условиям (6)

46. Способ понижения порядка системы, если известна часть первых интегралов.

Пусть имеется исходная система n диф. ур-ий первого порядка:

(1)

для которой известны k независимых первых интегралов: (k<n). Это означает, что:

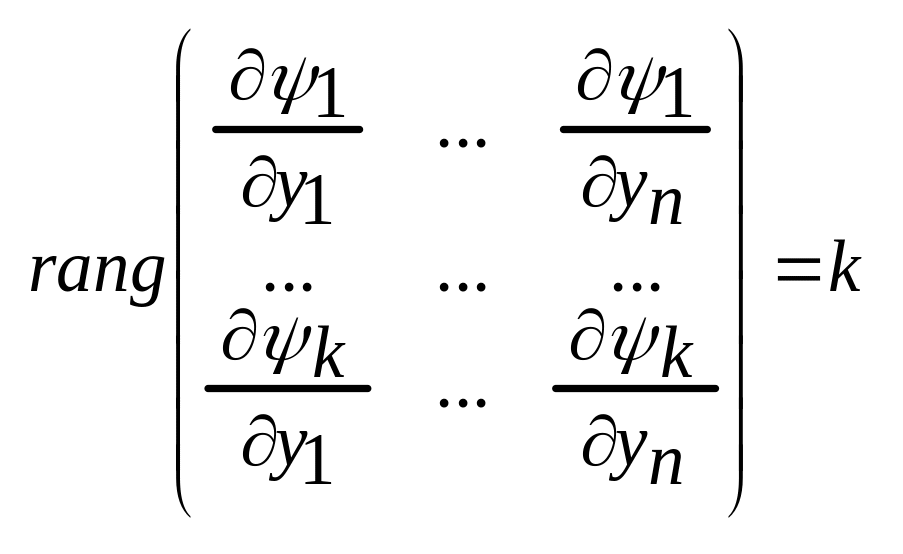
Предположим, что определитель из k первых столбцов и k строк не равен нулю:

(2)

В силу определения первых интегралов:

(3)

В силу условия (2) систему (3) можно разрешить относительно переменных . В результате получим:

(4)

Тогда в системе (1) можно взять последние (n-k) уравнений и подставить в них (4). Получим систему (n-k)-го порядка:

(5)