
- •Вариационный ряд
- •Распределение выборки
- •Несмещенные оценки дисперсии
- •Замечание
- •Состоятельность
- •Теорема Бореля
- •Замечание
- •Теорема Гливенко - Кантелли
- •Замечание
- •Гистограмма
- •Построение гистограммы
- •Замечание
- •Эффективность
- •Замечание
- •Метод моментов Пирсона
- •Достаточное условие состоятельности оценки, найденной по методу Пирсона
- •Метод максимального правдоподобия Фишера
- •Ди для математического ожидания (генеральной средней) µ при известной дисперсии σ2
- •Пример простой статистической гипотезы
- •Пример сложной статистической гипотезы
- •Замечание
- •Замечание
- •Минимаксный критерий
- •Критерий Бейеса
- •Регрессионный анализ
- •Замечание
- •Задачи регрессионного анализа
- •Аддитивная модель регрессии
- •Замечание
- •Уравнение множественной линейной регрессии
- •Проверка значимости уравнения множественной линейной регрессии
- •Несмещенная точечная оценка остаточной дисперсии
Гистограмма
Является выборочным аналогом плотности распределения.
Построение гистограммы
На числовой прямой выбирается определенный интервал [a,b), содержащий все элементы выборки (x1, x2,…,xn):
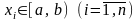 .
.
Интервал [a,b) разбивается на некоторое количество m непересекающихся интервалов (не обязательно одинаковой длины):
 ,
,
где a=r0<r1<r2<…<rm-1<rm=b.
Тем самым осуществляется группирование элементов выборки.
Для каждого интервала группировки
 определяется количество попавших в
него элементов выборки (x1,
x2,…,xn):
определяется количество попавших в
него элементов выборки (x1,
x2,…,xn):
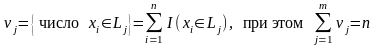 .
.
На каждом интервале , взятом как основание, строится прямоугольник, высота hj которого выбирается равной величине отношения статистической вероятности
 того, что наблюдаемый признак ξ
принял значение из данного интервала,
к длине этого интервала Δj=rj-rj-1:
того, что наблюдаемый признак ξ
принял значение из данного интервала,
к длине этого интервала Δj=rj-rj-1:
 .
.
Общая площадь построенных прямоугольников равна единице:
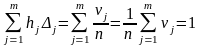 .
.
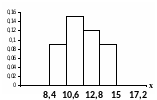
Ступенчатая ломаная линия, ограничивающая сверху полученную таким образом фигуру, называется гистограммой.
Аналитическое представление гистограммы:
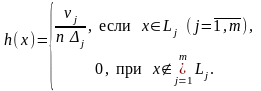 .
.
Пример
X(15)=(8,6; 16,2; 9,3; 10,1; 17; 13,5; 11,8; 12; 10,9; 13,2; 11,8; 13,4; 16,7; 12,4; 14)
Разобьем
интервал
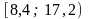 ,
в который попадают все элементы выборки,
на 4
интервала с длиной, равной
,
в который попадают все элементы выборки,
на 4
интервала с длиной, равной
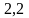 .
В интервале
.
В интервале
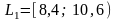 содержатся 3
элемента выборки, в
содержатся 3
элемента выборки, в
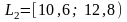 - 5,
в
- 5,
в
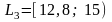 - 4
и в интервале
- 4
и в интервале
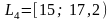 - 3
элемента.
- 3
элемента.
З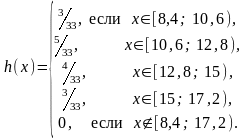 амечание
амечание
При построении гистограмм имеется свобода в выборе интервала [a,b), а также числа интервалов группировки m и точек разбиения r1, r2,…, rm-1. Если в этом отношении не следовать определенным правилам, то с ростом объема выборки n соответствующая гистограмма не всегда может приближаться к плотности распределения, в частности, если брать число интервалов группировки порядка n.
Достаточное условие состоятельности гистограммы
Если
наблюдаемый признак обладает непрерывной
плотностью распределения вероятностей
значений, то при неограниченном
возрастании числа интервалов группировки
m(n),
таком, что
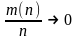 при
при
 ,
имеет место поточечная сходимость по
вероятности последовательности
гистограмм к кривой плотности
распределения.
,
имеет место поточечная сходимость по
вероятности последовательности
гистограмм к кривой плотности
распределения.
Замечание
Число интервалов группировки, определяемое по часто применяемой на практике формуле Стерджесса:
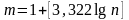 ,
,
удовлетворяет указанному условию сходимости, но вместе с тем не является единственно возможным и может быть задано иначе.
Пример использования формулы Стерджесса
Для
рассмотренной выборки X(15)
рекомендуемое число интервалов
группировки равно
 .
.
Точечная оценка неизвестного параметра распределения. Понятия состоятельности и несмещенности точечной оценки параметра распределения.
Точечной оценкой параметра θ распределения вероятностей генеральной совокупности называется всякая статистика θ*(x1,x2,…,xn), значение которой при любой выборке (x1, x2,…, xn) произвольного объема n из данной генеральной совокупности принимается в качестве приближенного значения рассматриваемого параметра.
Несмещенность
Статистика
θ*(x1,x2,…,xn)
называется несмещенной на некотором
подмножестве
точечной
оценкой
параметра θ
распределения
вероятностей
генеральной совокупности,
если для
каждого значения
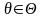 имеет место равенство
имеет место равенство
Mθ*(x1,x2,…,xn)=θ.
Замечание
Математическое ожидание оценки θ*(x1,x2,…,xn) вычисляется по распределению рассматриваемой статистики, определяемому заданным значением параметра θ.
Несмещенность — свойство оценок при фиксированном объеме выборки n, означающее отсутствие ошибки «в среднем», т.е. при систематическом использовании данной оценки.
Состоятельность
Статистика θ*(x1,x2,…,xn) называется состоятельной на некотором подмножестве точечной оценкой параметра θ распределения вероятностей генеральной совокупности, если, каково бы ни было значение ,
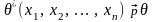 .
.
Замечание
Свойство состоятельности означает, что последовательность оценок θ*(x1,x2,…,xn) (n=1, 2,…) при неограниченном увеличении объема выборки n приближается (со сколь угодно высокой степенью достоверности) к значению параметра θ, т.е. для любого фиксированного >0
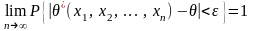 .
.
Для состоятельных оценок оправдано увеличение числа выборочных данных, поскольку это снижает до практически допустимых пределов вероятность ошибки при оценивании параметра. При отсутствии этого свойства оценка теряет практический смысл.
Для состоятельности оценки θ*(x1,x2,…,xn) параметра θ на подмножестве достаточно, чтобы при для любого математическое ожидание Mθ*(x1,x2,…,xn) стремилось к значению θ, а дисперсия Dθ*(x1,x2,…,xn) - к нулю.
Достаточность условий проверяется с помощью неравенства Чебышева:
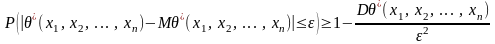 .
.
Сравнение точечных оценок неизвестного параметра распределения. Понятия эффективной и асимптотически эффективной точечной оценки параметра распределения.
Сравнение точечных оценок параметра распределения вероятностей
Так как полученные для одного и того же объема выборки различные оценки неизвестного параметра распределения вероятностей носят случайный характер, целесообразно сравнивать не их отклонения от этого параметра как таковые, а осредненные по соответствующему распределению вероятностей значения (математические ожидания) удобной для применения неотрицательной функции отклонения.
Естественно при таком подходе полагать, что чем меньше оценка отклоняется в указанном смысле от параметра, тем более она пригодна.
Точечная
оценка
 на некотором
подмножестве
считается
лучше точечной
оценки
на некотором
подмножестве
считается
лучше точечной
оценки
 в смысле среднеквадратического подхода,
если для любого
в смысле среднеквадратического подхода,
если для любого
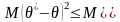 ,
,
и хотя бы при одном допустимом значении θ это неравенство строгое.
