Решение задач I типового варианта

Вычислить определенные интегралы с точностью до двух знаков после запятой.

1. ▲

. ▼

2. ▲

. ▼

3. ▲

,

,

,

. ▼

4. ▲

. ▼

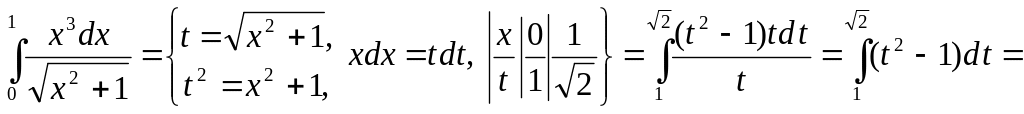
5. ▲

. ▼

6. ▲

. ▼

7. ▲

. ▼

6. Вычисление несобственных интегралов

Определенный интеграл рассматривался при следующих предположениях:

• отрезок интегрирования конечен,

• подынтегральная функция на этом отрезке непрерывна.

При таких предположениях этот интеграл называется интегралом в «собственном смысле», ил «собственным» интегралом. В том же случае, когда отрезок интегрирования бесконечен или конечен, но подынтегральная функция на этом отрезке терпит разрыв, интеграл называется интегралом в «несобственном смысле», или «несобственным» интегралом.

I. Несобственные интегралы с бесконечными пределами интегрирования (первого рода) определяются посредством предельного перехода:

,

,

,

где – произвольное вещественное число.

Замечание. При вычислении несобственных интегралов с бесконечным промежутком интегрирования часто пользуются символическим равенством

,

где .

Если существует определенный конечный предел в правой части, то несобственный интеграл называется сходящимся, а функция в этом случае называется интегрируемой на бесконечном промежутке.

Если же этот предел бесконечен или не существует, то интеграл называется расходящимся.

Если отыскать первообразную функцию трудно или если она в конечном виде не может быть вычислена, то существуют признаки, позволяющие решить вопрос о сходимости или расходимости несобственного интеграла.

II. Несобственные интегралы от функций с бесконечными разрывами также определяются посредством предельного перехода:

а) Если функция неограниченно возрастает, т. е. , когда , то

;

если функция неограниченно возрастает, т. е. , когда , то

.

б) Если подынтегральная функция перестает быть ограниченной внутри отрезка интегрирования, например , то эту точку «вырезают», а интеграл определяют в предположении, что – первообразная , так

,

где изменяются независимо друг от друга.

Если оба предела в правой части существуют и конечны при не зависящем друг от друга стремлении к нулю, то несобственный интеграл от неограниченной функции называется сходящимся, в противном случае – расходящимся.

Задача 6.1. Найти следующие несобственные интегралы: 1) ; 2) ; 3) ; 4) .

Пояснить решение геометрически.

1) ▲ .

Следовательно, данный несобственный интеграл сходится.

Геометрически, в прямоугольной системе координат, всякий определенный интеграл дает алгебраическую сумму площадей, ограниченных кривой , двумя вертикальными прямыми и осью .

Поэтому, построив кривую , ее ординаты в точках , получим криволинейную трапецию , площадь которой

.

При получим трапецию с бесконечным основанием, которая имеет конечную площадь .

y

A

1

B

O 1 b x ▼

2) ▲

.

Следовательно, несобственный интеграл сходится.

Геометрически интеграл от функции в пределах выражает площадь криволинейной трапеции , а данный несобственный сходящийся интеграл выражает площадь бесконечной криволинейной трапеции, которая неограниченно простирается влево и вправо и вместе с тем имеет конечную величину .

y

1

A B

a O 1 b x ▼

3) ▲ ,

т. е. несобственный интеграл расходится.

y

A

B

O ε b =1 x

Геометрически полученный результат указывает, что площадь криволинейной трапеции

неограниченно возрастает. ▼

4) ▲

.

Данный несобственный интеграл сходится.

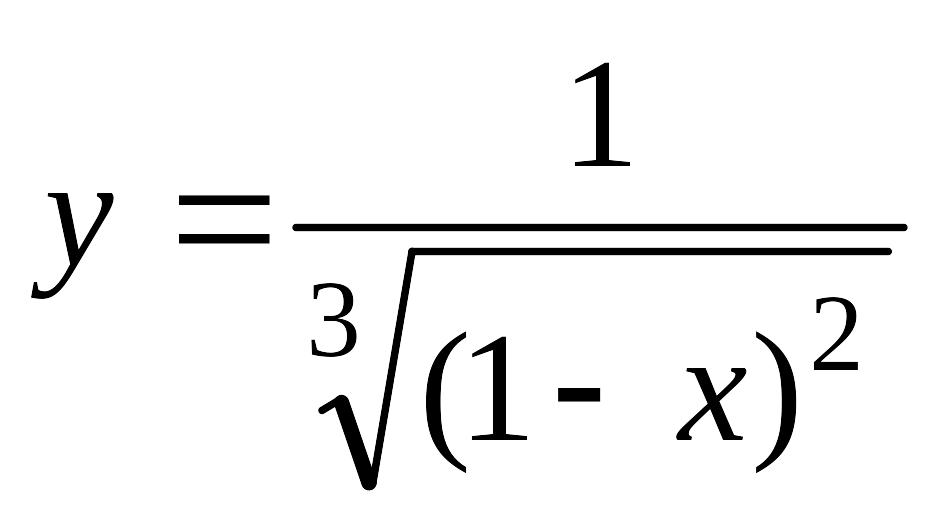
y

P Q

1

A B

ε ε

a O ε 1 η b x

Прямая является вертикальной асимптотой графика подынтегральной функции . Интегралы от этой функции в пределах выражают площади криволинейных трапеций . При эти трапеции неограниченно простираются вверх и вместе с тем имеют конечные площади, сумма которых равна найденному значению данного несобственного сходящегося интеграла. ▼