11.2. Математический аппарат описания импульсных систем

 

Для исследования импульсных систем используется дискретный математический аппарат, основным элементом которого является понятие решетчатой функции.

Решетчатой функцией или в сокращенной форме записи , называется функция, значения которой определены в дискретные моменты времени , где n – целое число, а – период повторения (дискретизации). Операция замены непрерывной функции решетчатой

показана на рис. 6.

Решетчатые функции такого вида определены только в дискретные моменты времени (сокращенно ), и формируются из непрерывных функций: при . Рассматривают так же смещенные решетчатые функции (последовательность 3): при , где — относительное смещение, .

Решетчатая функция не обязательно формируется из некоторой исходной непрерывной функции. Любая числовая последовательность, значения которой определены в дискретные равноотстоящие моменты времени, может быть представлена в виде решетчатой функции. И если прямая задача определения решетчатой функции из непрерывной имеет единственное решение, то обратная задача – формирование непрерывной функции из решетчатой — не имеет однозначного решения.

Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции.

Основная огибающая может быть получена, как результат решения дифференциального уравнения наименьшего порядка и должна содержать гармоники наименьшей частоты.

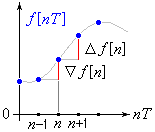
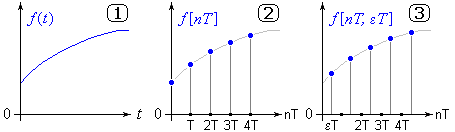
Рис. 6. Решетчатые функции

 

Дифференцирование и интегрирование решетчатых функций

 

Аналогом первой производной для решетчатой функции является либо первая прямая разность:

,

либо первая обратная разность:

Аналогов второй являются вторые разности. Прямая:

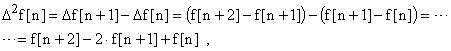
и обратная:

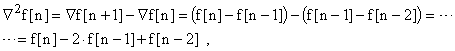
По аналогии могут определяться и высшие разности:

.

,

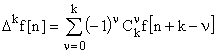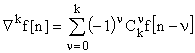где:

Очевидно, что если определена только для положительных , то для все обратные разности равны нулю.

Аналогом интеграла непрерывной функции для решетчатой является неполная сумма:

,

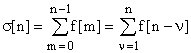и полная сумма:

.

 

Разностные уравнения

 

Аналогом дифференциальных уравнений для импульсной системы является уравнение в конечных разностях или разностное уравнение (РУ):

,

Разностное уравнений может быть составлено и в прямых разностях. Если раскрыть разности, то уравнение будет иметь вид:

(1)

где

,

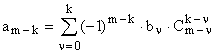Разностные уравнения легко машинизируются и для их расчета можно составлять рекуррентный алгоритм.

Учтем запаздывание передаточной функцией звена чистого запаздывания и вынесем теперь уже изображение дискретной последовательности в уравнении (1) за скобку:

,

введем обозначение и перепишем уравнение:

.

Решая это уравнение, для чего его левая часть приравнивается к нулю, можно получить общее решение, т.е. переходную составляющую в виде:

.

где: — корни выражения в скобках; а — произвольные постоянные.

Вид решения левой части определяет условие устойчивости для систем, описанных с помощью разностных уравнений:

.

 

Z-преобразование

 

Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа:

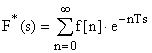
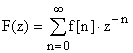
которое называется Z-преобразованием при подстановке , и связывает изображение с оригиналом.

Z-преобразования (изображения) типовых решетчатых функций и типовых непрерывных передаточных функций сведены в таблицы. Определены правила и теоремы для математических манипуляций с ними.