Законы распределения: ряд распределения, функция распределения, плотность распределения.
Заданное соответствие между возможными значениями ДСВХ и их вероятностями называется законом распределения дискретной случайной величины ; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности:
Х |
x1 |
x2 |
… |
xn |
р |
p1 |
p2 |
… |
pn |
Эта таблица называется рядом распределения
Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора.
Свойства
непрерывна справа:[1]
не убывает на всей числовой прямой.
.
.
Распределение случайной величины
однозначно определяет функцию
распределения.
Верно и обратное: если функция
удовлетворяет четырём перечисленным
выше свойствам, то существует вероятностное
пространство и определённая на нём
случайная величина, такая что
является её функцией распределения.
По определению непрерывности справа,
функция
имеет правый предел
в любой точке
,
и он совпадает со значением функции в
этой точке.
В силу неубывания, функция
также имеет и левый предел
в любой точке
,
который может не совпадать со значением
функции. Таким образом, функция
либо непрерывна в точке, либо имеет в
ней разрыв первого рода.
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
Числовые параметры распределения ( матожидание, дисперсия, начальные и центральные моменты).
Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.
Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .
Математическое ожидание дискретной случайной величины x , имеющей распределение
x1 x2 ... xn
p1 p2 ... pn
называется величина
,
если число значений случайной величины
конечно.
Если число значений случайной величины
счетно, то
.
При этом, если ряд в правой части равенства
расходится, то говорят, что случайная
величина x не имеет математического
ожидания.
Математическое ожидание непрерывной
случайной величины с плотностью
вероятностей px (x) вычисляется по формуле
.
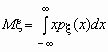При этом, если интеграл в правой части
равенства расходится, то говорят, что
случайная величина x не имеет математического
ожидания.
Если случайная величина h является функцией случайной величины x , h = f(x), то
.
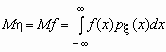
Аналогичные формулы справедливы для функций дискретной случайной величины:
,
Основные свойства математического ожидания:
математическое ожидание константы равно этой константе, Mc=c ;
математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и b справедливо: M(ax + bh ) = a M(x )+ b M(h );
математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).
Начальным моментом k-го порядка случайной величины x называется математическое ожидание k-й степени случайной величины x , т.е. a k = Mx k.
Центральным моментом k-го порядка случайной величины x называется величина m k, определяемая формулой m k = M(x - Mx )k.
Заметим, что математическое ожидание случайной величины - начальный момент первого порядка, a 1 = Mx , а дисперсия - центральный момент второго порядка,
a 2 = Mx 2 = M(x - Mx )2 = Dx .
Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:
m 2=a 2-a 12, m 3 = a 3 - 3a 2a 1 + 2a 13.
Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = Mx , то все ее центральные моменты нечетного порядка равны нулю.
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )2.
Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.
Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам
,
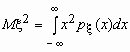
Для определения меры разброса значений случайной величины часто используется среднеквадратичное отклонение , связанное с дисперсией соотношением .
Основные свойства дисперсии:
дисперсия любой случайной величины неотрицательна, Dx 0;
дисперсия константы равна нулю, Dc=0;
для произвольной константы D(cx ) = c2D(x );
дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ± h ) = D(x ) + D (h ).