Решение типовой задачи.
Исследовать на
экстремум функцию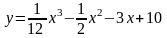
и определить интервалы ее возрастания
и убывания, найти точки перегиба графика
этой функции и определить интервалы
выпуклости и вогнутости графика.
Построить график.
Решение.
Чтобы найти точки экстремума, вычисляем производную и приравниваем ее к нулю, решаем полученное уравнение:
Корни
уравнения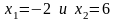
- критические точки. Эти точки разбивают
числовую ось на три интервала:
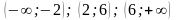
Производную
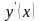можно представить так:
.
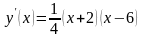И
з
последнего равенства видно, что в первом
интервале
,
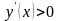во втором
и в третьем интервале
.
Следовательно, в первом и третьем
интервалах функция возрастает, а во
втором убывает. Так как в критической
точке
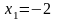производная меняет знак с плюса на
минус, то в этой точке функция имеет
максимум. А в силу того, что в точке
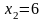производная
меняет знак с минуса на плюс, функция
имеет минимум в этой точке. Вычислим
значение функции в этих точках:
.
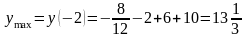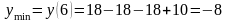
Точка B(6;-8)- точка минимума.
Точка
A(-2;13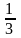
)-
точка максимума.
Чтобы найти точки перегиба, интервалы выпуклости и вогнутости, находим вторую производную, приравниваем ее нулю и решаем полученное уравнение.
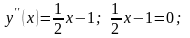
x-2=0;
x=2
– критическая точка второго рода. Эта
точка разбивает числовую ось на два
интервала:
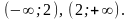Как видно, в первом случае
,
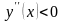во втором -
Следовательно,
в первом интервале график функции –
выпуклый, во втором – вогнутый. Так как
производная
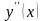при переходе через точку х=2 меняет свой
знак, то х=2 есть абсцисса точки перегиба
графика. Вычисляем ординату этой точки:
;
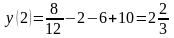Таким образом, точка
–
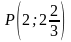точка перегиба графика функции.
6. В задачах 1-20 требуется найти указанные неопределенные интегралы:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Решение типовых задач
а) Найти интеграл
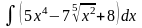
Решение:
Воспользуемся следующими свойствами неопределенного интеграла:
1. постоянной множитель можно выносить за знак интеграла, то есть
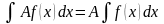
2. Неопределенный интеграл от суммы (разности) функций равен сумме (разности) интегралов от каждой функции в отдельности, то есть
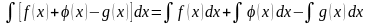
Преобразуем подынтегральную функцию в интервале (1) и воспользуемся формулой 1 из таблицы основных неопределенных интегралов:
=
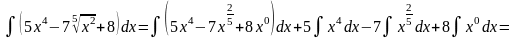
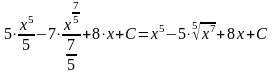
б) Найти интеграл
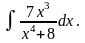
Решение:
Воспользуемся
подстановкой
.
Тогда
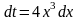,откуда
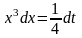.Таким
образом,
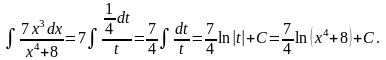
в) Найти интеграл
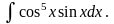
Решение:
Воспользуемся
подстановкой
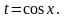
Тогда
.
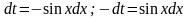Таким образом,
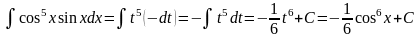
7. В задачах 1-20 вычислить площадь фигуры, ограниченной параболой и прямой. Сделать чертеж и заштриховать искомую площадь.
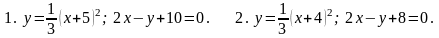
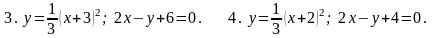
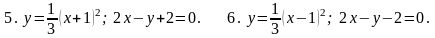
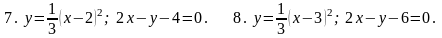
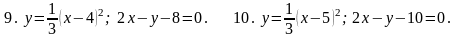
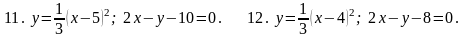
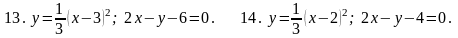
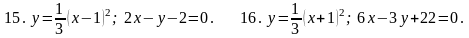
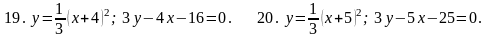
Решение типовой задачи
Задача. Вычислить площадь фигуры, ограниченной параболой
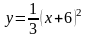и прямой
.
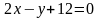Решение:
Площадь
фигуры, ограниченной сверху непрерывной
кривой у=f(х);
снизу – непрерывной кривой
,
слева– прямой х=а,
справа– прямой х=b,
вычисляется по формуле
Если кривые у=f(х) и образуют замкнутую линию, то точки а и b совпадают с абсциссами точек пересечения этих кривых. Найдем точки пересечения заданных параболы и прямой. Для этого решим систему их уравнений:
Приравниваем значения у из обоих уравнений:
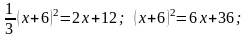
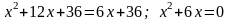
Отсюда
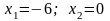.Таким
образом, парабола пересекается с прямой
в точках А(-6;0) и В(0;12).
Искомая фигура изображена на рисунке.
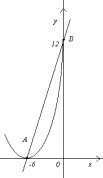
Из формулы (1) следует, что площадь фигуры равна
=
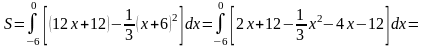
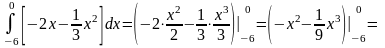
Следовательно, искомая площадь равна 12 кв. ед.
8.
Требуется
составить дифференциальное уравнение
динамики развития некоторого биологического
вида и найти решение этого уравнения.
Состояние
популяции (в простейшем понимании -
стада) можно охарактеризовать массой
m
этой популяции (то есть весом всего
стада), причем масса m
является функцией времени m=m(t)
, Считая, что скорoсть
прироста биомассы пропорциональна
биомассе популяции с коэффициентом
k=k(t)
и что известна начальная биомасса m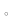
(при t=0),
найти величину биомассы в момент t=T.
1.
m
=
12; T=2; k(t)=
.
2.
m
=18; T=18; k(t)=
.
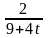3.
m
=9; T=8; k(t)=
.
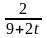4.
m
=12;
T=2; k(t)=
.
5.
m
=14; T=3; k(t)=
.
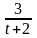6.
m
=10;
T=2; k(t)=
.
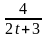7.
m
=1; T=12; k(t)=
.
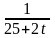8.
m
=5; T=4; k(t)=
.
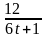9.
m
=18; T=2; k(t)=
.
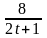10.
m
=8; T=2; k(t)=
.
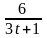11.
m
=
2; T=2; k(t)=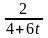
.
12.
m
=8; T=18; k(t)=
.
13.
m
=19; T=8; k(t)=
.
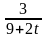14.
m
=22;
T=2; k(t)=
.
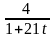15.
m
=24; T=3; k(t)=
.
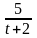16.
m
=4;
T=2; k(t)=
.
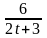17.
m
=7; T=12; k(t)=
.
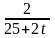18.
m
=15; T=4; k(t)=
.
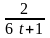19.
m
=8; T=2; k(t)=
.
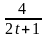20.
m
=18; T=2; k(t)=
.
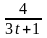