26. Отображения мн-в (функции). Предел функции в точке. Арифметические св-ва пределов.

Понятие отображения мн-в (функции) в курсе матем. Анализа вводится чаще всего на основе понятия соответствия, которое считается первичным, и опред

Опр.1. Отображением А во мн-во В наз. Соответствие f, в котором каждому элементу  сопоставляется единственный элемент b из В.

Символическая запись: (отображение “в”) или, коротко f: A→B.

Множество А при этом наз. областью задания (определения) отображения f, а элементы мн-ва А наз. аргументами отображения f. Элемент b=f(a) из мн-ва В наз. значением отображения f на аргументе а или образом элемента а в отображении f.

Термин”функция” применяется как синоним термину”отображение”. В том случае, когда мн-ва Аи В состоят из действительных чисел: , вместо термина “отображения” применяют термин “числовая функция” или “вещественная функция”. Мы же в этом случае все равно будем говорить: ”функция”.

Функции могут быть заданы таблично, графически, аналитически. В случае аналитического способа задания иногда мн-во А не указывается явно. При этом подразумевается, что функция задана на мн-ве всех тех x из R, для которых данное аналитическое выражение имеет смысл и приводит после выполнения всех указанных операций к числу из R. Область определения функции f в подобном случае будем обозначать D(f).

Прежде чем привести опр. предела функции сделаем два зам. 1. Из всего многообразия вариантов предела функции

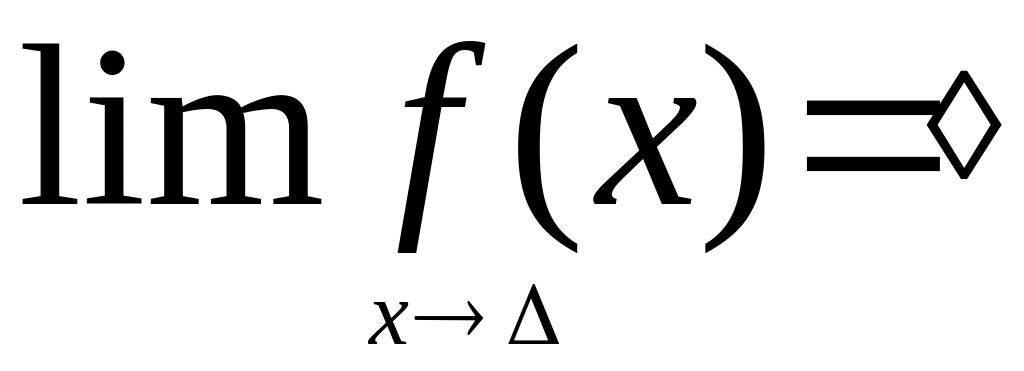
//а) - на месте ◊ и ∆ стоят действительные числа; б) – на месте ◊ и ∆ стоят какие-либо из символов: ∞, +∞, -∞; в) – на месте ∆ стоит действительное число, а на месте ◊ - стоит из символов: ∞, +∞, -∞,; г) – на месте ∆ стоит один из символов: ∞, +∞, -∞, а на месте ◊ - действительное число// мы остановимся только на основном варианте а). 2. В отличие от школьного курса математики, в котором при определении предела функции в точке х₀ предлагается, что функция определена на всех ближайших х слева и справа от х₀, мы изложим теорию без этого ограничения, т.е. даже и в том случае когда мн-во D(f) в любой δ – окрестности точки х₀ не сплошное, “дырявое”. Чтобы достичь указанной общности определения предела функции применяют либо понятие “предельная точка мн-ва”, либо понятие “точка прикосновения мн-ва”. Мы будем использовать второе опр.

Опр.2. Пусть А – непустое числовое мн-во. Говорят, что х₀ – точка прикосновения мн-ва А, если существует хотя бы одна послед-ть (a_n) со св-ми:

Ясно, что каждая точка из мн-ва А является точкой прикосновения этого мн-ва А. Вместе с тем некторые мн-ва могут иметь точки прикосновения и не принадлежащие им. Например, 0 – точка прикосновения мн-ва А=(0,1), т.к.

Опр.3. (Гейне) Пусть х₀ – точка прикосновения области определения D(f) функции f. Число а наз. пределом функции f в точке х₀, если для каждой послед-ти аргументов (х_n), сходящейся к х₀, соответствующая послед-ть значений функции (f(x)) имеет пределом (всегда одно и тоже) число а.

Символическая запись опр.:

Обозначение предела функции f в точке х₀:

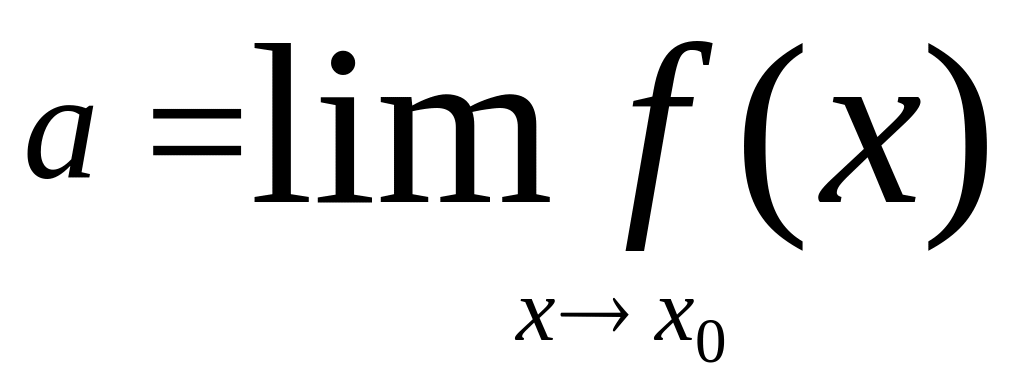
Пример:

Т.1. Функция может иметь в точке на более одного предела.

Т.2. Если существуют конечные пределы функций f и g в точке х₀, причем х₀ – точка прикосновения мн-ва D(f)∩D(g), то в ней существуют пределы функций f+g, f-g, f*g и

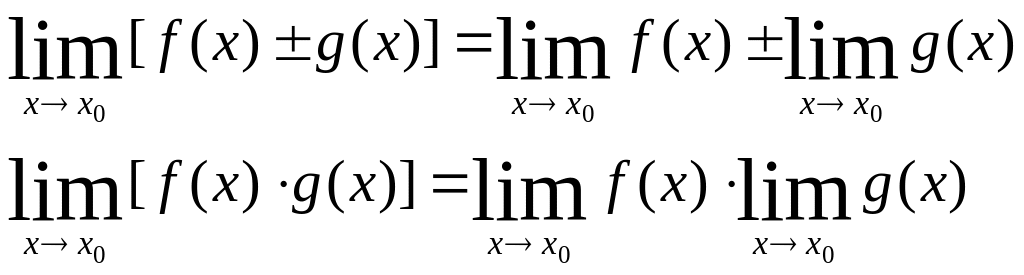
Т.3. Если, в условиях Т.2. , кроме того 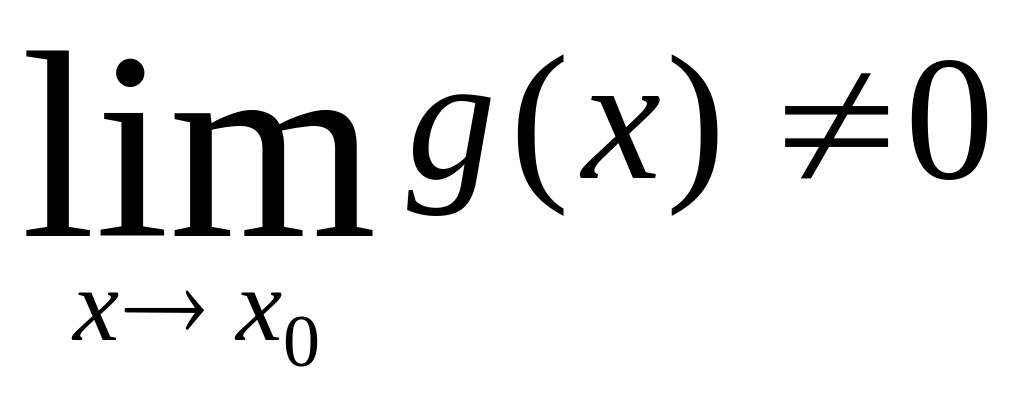,то в точке х₀ существует предел функции f/g, причем

Док-во: Т.к. по условию х₀ – точка прикосновения мн-ва D(f)∩D(g), а, как известно, (1)

то нетрудно убедиться, что существует хотя бы одна послед-ть аргументов функции f/g, сходящаяся к х₀ // достаточно взять послед-ть которая существует в силу опр.2.; для нее найдется номер n₀ со св-вом , т.к. в противном случае для некоторой послед-ти (хn_k)

что противоречит дополнительному условию в Т.3; тогда послед-ть чисел хn₀, xn₀+1, …, xn₀+n, … - искомая//.

Пусть (х_n) – произвольная сходящаяся к х₀ послед-ть чисел из D(f/g). В силу равенства (1) . Тогда из условия существования предела Аналогично: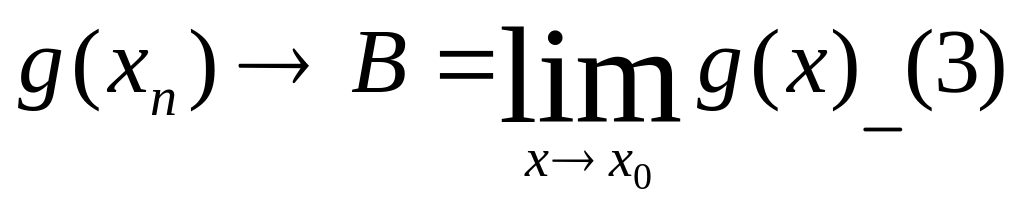

Заметим, что В≠0 и . Тогда по Т.4(. Если послед-ть (x_n) имеет пределом число а, а послед-ть (y_n) – b, причем b≠0, то существует предел послед-ти (x_n/y_n), равный a/b.), в силу условий (2) и (3), имеем f(x_n)/g(x_n)→A/B. По опр.3. последнее означает, что число А/В – предел функции f/g в точке х₀.

Опр.4.(Коши) Число А наз. пределом функции f(x) в точке х₀, если для любого сколь угодно малого числа ε>0 найдется такое число δ>0, что для всех х≠х₀, х€Х, удовлетворяющих неравенству │х-х₀│<δ, выполняется неравенство │f(x)-A│<ε.

Зам. Во многих учебниках опр. предела дается на основе предельной точки.

Опр.5. х₀ – предельная точка D(f), если существует послед-ть (х_n) такая, что x_n→x₀, x_n ≠x₀ и x_nЄD(f).

27. Непрерывность функции в точке. Свойства функций непрерывных на отрезке.

Опр.1. Функция f с областью определения D(f) наз. непрерывной в точке х₀, если у нее в этой точке существует предел, совпадающий с f(x₀).

Многие св-ва, касающиеся непрерывности в точке, автоматически следуют из соответствующих теорем о конечных пределах.

Теорема 1. Если функции: f и g непрерывны в точке х₀, то в этой точке непрерывны и функции f±g, f·g, а при g(x₀)≠0 и функция f/g.

Опр.2. Функция f наз. непрерывной на мн-ве Е, если она непрерывна в каждой точке из мн-ва Е //заметим, что при этом необходимо выполнятся ЕcD(f)//.

Т.2.(Больцано – Коши) Если функция f определена и непрерывна на отрезке [а, b] и на его концах принимает значения разных знаков, тогда существует точка с, кот. принадлежит интервалу (а, в) со св-вом f(c)=0.

Док-во: Разделим отрезок (а, в) пополам точкой (а+в)/2. Можно сказать, что в этой точке функция обратится в 0, тогда обозначим с=(а+в)/2 и доказательство закончено. Поэтому будем считать, что значение в этой точке f≠0. Тогда на концах

одного из отрезков [а;(а+b)/2] (если f((a+b)/2)>0) или [(а+Ь)/2;b] (если f((a+b)/2)<0) функция принимает значение разных знаков. Обозначим этот отрезок через [а₁,b₁], тогда будем иметь как и на [a,b], функция f принимает на левом конце сегмента отрицательное значение, а на правом – положительное.

Р азделим пополам отрезок [а₁,b₁] и вновь отбросим тот случай, когда f((a₁,b₁)/2)=0, тогда Т.доказана. Обозначим через [а₂, b₂]ту половину [a₁,b₁], на концах которой функция принимает значения разных знаков. Далее делим [a₂,b₂] и т.д. Тогда имеем послед-ть вложенных отрезков [a_n,b_n]c[а₂, b₂]с [а₁, b₁]c[a,b], для которой

(1)

Продолжим дальше деление отрезка пополам, при этом возможны 2 варианта:

1. либо мы после конечного числа шагов наткнемся на точку деления, в которой функция обращается в 0 и тогда теорема доказана.

2. либо продолжение деления продолжается неограниченно. Таким образом выполнены все условия принципа стягивающихся отрезков (т.Кантора) по этому принципа последовательности (а_п) и (b_п) стремятся к общему пределу.

В силу непрерывности функции f в точке с тогда при n→∞ f(a_n)→f(c) и f(b_n)→f(c). Учитывая это, по Т. о предельном переходе в неравенстве, из неравенств(1) получаем: f(c)≤0 и f(c)≥0. Следовательно, f(c)=0 и точка с – искомая.

Случай, когда f(a)>0 и f(b)<0 можно изложить по аналогии с рассмотренным. Можно также свести его к рассмотренному путем перехода от функции f к непрерывной на [a,b] функции φ(x)= - f(x).

Т.3. (о промежуточных значениях Б-К) Если f непрерывна на отрезке [а,b] и на его концах принимает неравные между собой значения A и В соответственно.

Тогда, для любого числа С, лежащее между А и В, найдется такая точка с со св-вом f(c)=C.

Док-во: Пусть для определенности А<В. Вспомогательная функция h(x)=f(x)-C, очевидно, непрерывна на [a,b]. Т.к., кроме того h(a)=f(a)-C=A-C<0, h(b)=f(b)-C=B-C>0, то по Т.2. существует с€(a,b) со св-вом h(c)=0, т.е. f(c)-C=0 или f(c)=C.

Следующие два основных св-ва непрерывных на сегменте функций приводим здесь без док-в.

Т.4.(1-я теорема Вейерштрасса). Каждая непрерывная функция f на отрезке [а,b] ограничена на нем.

Док-во: (ограниченности сверху) Пусть y=f(x) не ограничена сверху на[a,b]

возникла последовательность (x_n) - ограниченная числовая послед-ть (т.к. она в [a,b]). По Т.(Б.-К.) существует (xk_n) – подпослед-ть: xk_n – сходится к х₀

а≤x_n≤b=> a≤xk_n≤b=> по Т. о предельном переходе в неравенствах следует, что a≤x₀≤b=>x₀€[a,b]=>f- непрерывна в точке х₀, а по условию нерерывности следует, что f(xk_n)→f(x₀), следовательно (f(xk_n)) – сходящаяся числовая послед-ть => она ограничена(в частности ограничена сверху) (*)=>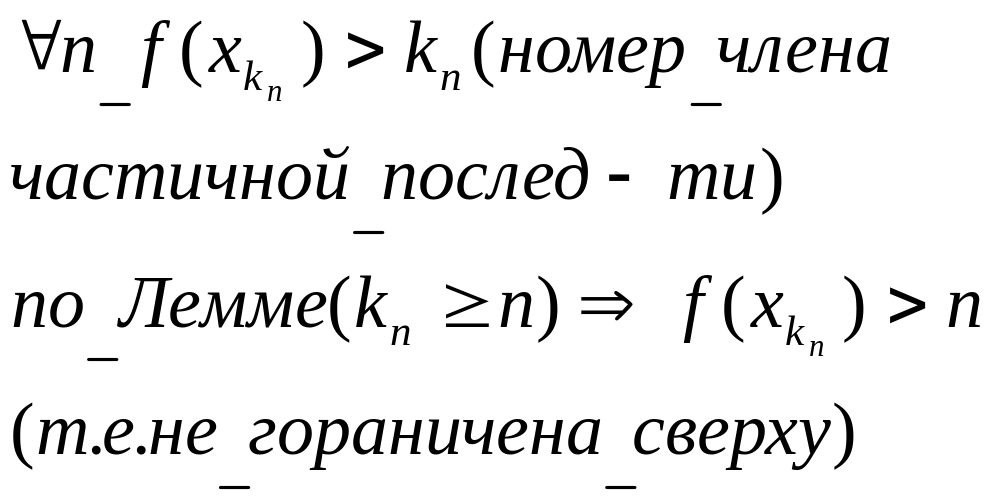 предположение не верное, т.е. f(x_n) – ограничено сверху.

Аналогично для ограниченности снизу(y=-f(x))

Теорема 5 (2-я т. Вейерштрасса). Если функция непрерывна на отрезке [а,b], то она принимает на нем наименьшее и наибольшее значение.(т.е. найдутся такие х₁,х₂, что f(x₁)≤f(x)≤f(x₂)/

Док-во: По т.4 функция ограничена на отрезке [а,b], в частности ограничена сверху, т.е сверху ограничено множество значений функций.

Обозначим М= Sир Е (f). Будем доказывать, что число М является значением функции, х₀:f(х₀)=М (МОП): по опр.2 :f(x)<М УхЄ[а.b] (1)

Временно допустим, что f(х)<М Ух€[а,b]/Тогда введем вспомогательную функцию g(х)

g(x)=1/(M-f(x)). Тогда по Т.1 функция g(х) непрерывна на [а,b] и по Т.4 ограничена на этом отрезке.

Тогда существует число Р>0: |g(х)│=g(x)=1/(М-f(х))≤р.

Последнее неравенство означает, что число М- 1/р≤М Ух € [а,b] является мажорантой множества Е(f), что невозможно, т.к. М=Sир Е (f)=>В (1) равенство имеется, т.е. существует х_о:f(хо)=М значит М -наибольшее значение функции.