Общее уравнение динамики имеет вид

или .

Здесь - работа задаваемых сил на возможном перемещении системы, а вектор возможного перемещения представляет собой синхронную вариацию радиуса-вектора .

После соответствующего преобразования скалярного произведения придаем общему уравнению динамики вид

. (14.14)

Ограничим произвольность выбора путей сравнения условием пересечения действительной траектории и кривой сравнения в момент времени и , т.е. условием, чтобы при и (рис. 14.2)

. (14.15)

Кривые сравнения должны выбираться из класса дважды дифференцируемых функций. Интегрируя равенство (14.14) в пределах ( , получим криволинейный интеграл:

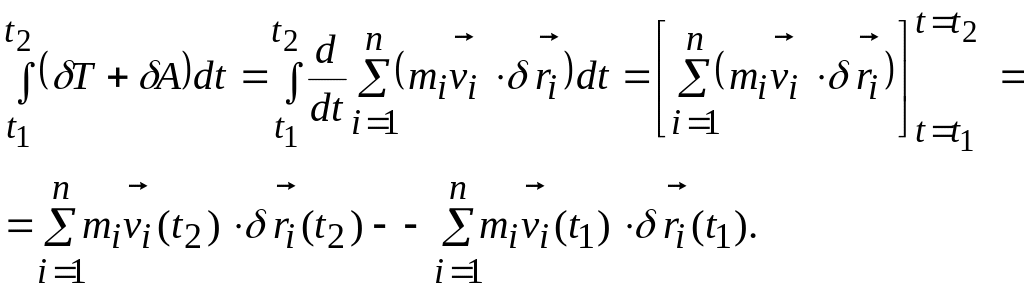
Так как по условию (14.15) вариация радиуса-вектора на границах равны нулю, то имеем

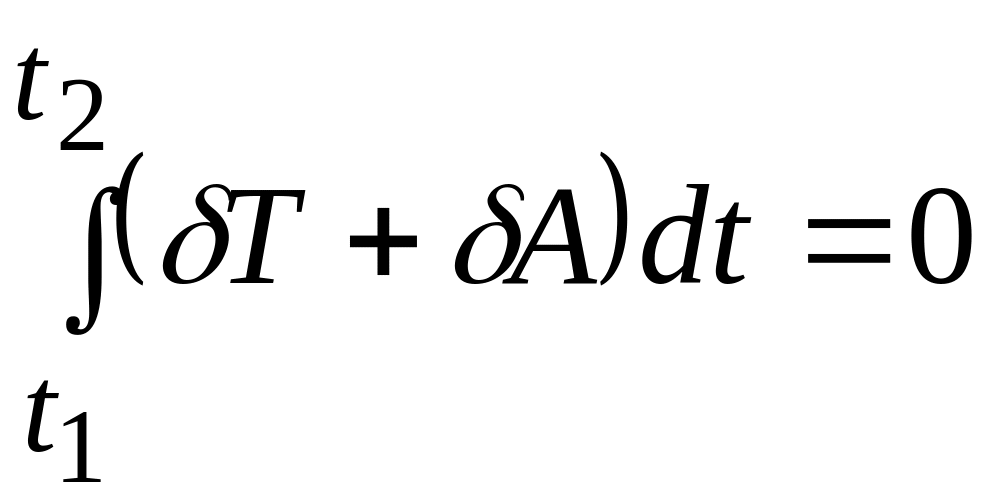. (14.16)

Рис. 14.2

Это уравнение выражает принцип Гамильтона-Остроградского: действительное движение механической системы с голономными двухсторонними идеальными связями отличается от всех иных возможных ее движений, удовлетворяющих условию (14.15), тем, что только для действительного движения выполняется равенство (14.16).

В случае, если раздельно рассматривать работу задаваемых консервативных и неконсервативных сил, уравнение (14.16) можно представить в следующем виде:

,

где - элементарная работа консервативных сил, а - элементарная работа неконсервативных сил. Так как , имеем

.

Учитывая, что

,

где L – функция Лагранжа, выраженная в обобщенных координатах, получаем

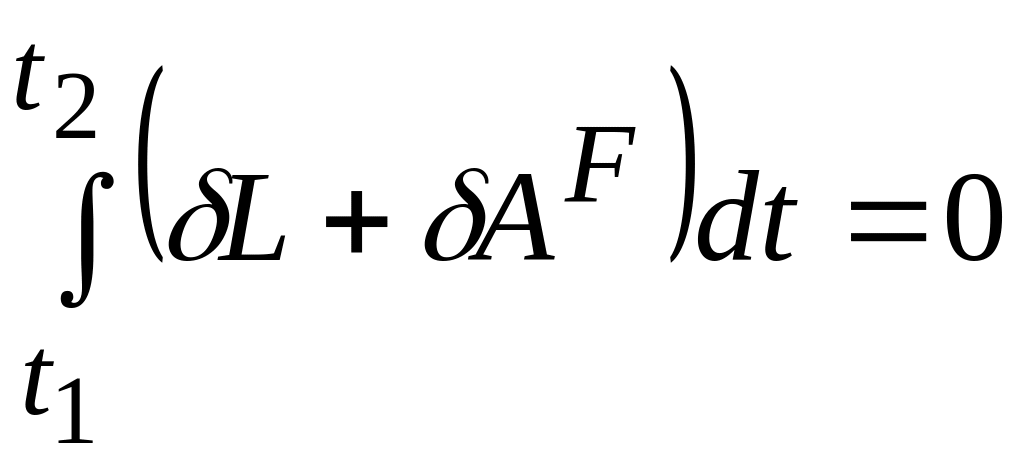. (14.17)

Для консервативной системы выражение принципа Гамильтона-Остроградского имеет вид

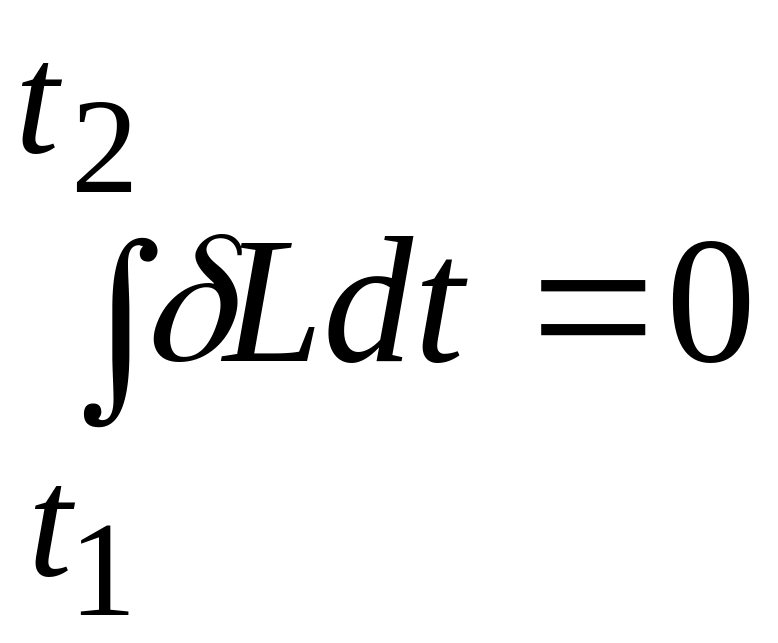. (14.18)

Введем обозначение

, (14.19)

где величина S называется действием по Гамильтону.

Размерность величины S есть работа, умноженная на время (единицы в системе МКС - , в технической системе - ).

В том случае, если система находится только под действием консервативных сил и при этом концы временного интеграла и не варьируется, т.е. , уравнение принципа Гамильтона-Остроградского принимает вид

, (14.20)

или в развернутом виде

. (14.21)

Поэтому принцип Гамильтона-Остроградского может быть сформулирован еще так: действительное движение консервативной механической системы таково, что вариация интеграла S при фиксированных значениях и равна нулю, или действительное движение консервативной системы в промежутке от и таково, что действие по Гамильтону имеет стационарное значение.

Равенство (14.20) является необходимым условием экстремума действия S. Из этого следует, что из всех возможных движений изображающей точки от ее положения в момент до ее положения в момент действительным является то движение. При котором интеграл (14.19) имеем экстремум: максимум или минимум, или стационарное значение, отличное от экстремума.

Пример. В эпициклическом механизме кривошип с противовесом вра­щается под действием приложенного к нему момента М (рис. 14.3, а). Момент инерции кривошипа с противовесом относительно оси его вращения равен . Центр тяжести бегущей шестерни и кривошипа с противовесом находится на оси вращения кривошипа. Расстояние между осями шестерен равно l. Бегущая шестерня имеет радиус , массу и момент инерции относительно ее оси . Определить, пренебрегая трением, угловое ускорение кри­вошипа и окружное усилие в точке соприкасания шестерен.

Рис. 14.3

Решение. Рассматриваемая механическая система имеет одну степень сво­боды. За обобщенную координату системы примем угол поворота кривошипа φ, отсчитанным от горизонтали.

Для определения углового ускорения кривошипа с противовесом применим уравнение Лагранжа второго рода:

.

Чтобы воспользоваться этим уравнением, определим кинетическую энергию системы как функцию обобщенной координаты φ и обобщенной скорости , равной угловой скорости кривошип ω.

Кинетическая энергия системы равна сумме кинетической энергия кривошипа с противовесом, вращающегося вокруг неподвижной оси, и кинети­ческой энергии бегущей шестерни, совершающей плоское движение.

По формуле,

.

По формуле,

.

Скорость центра масс шестерни

.

Угловую скорость бегающей шестерни определим с помощью мгно­венного центра скоростей, находящегося в точке В соприкасания шестерен (рис. 14.3, б):

.

Подставим значения и :

.

Кинетическая энергия системы

.

Из этого выражения следует, что кинетическая энергия системы зависит от обобщенной скорости и не зависит от обобщенной координаты φ, т. е. от положения механизма. Найдем производные:

; (а)

. (б)

На механизм действуют задаваемые силы: сила тяжести движущихся частей , приложенная в точке О, и вращающий момент М, приложенный к кри­вошипу.

Чтобы найти обобщенную силу соответствующую обобщенной координате φ, сообщим системе возможное перемещение, сообщив углу φ приращение δφ. Составим сумму элементарных работ задаваемых сил на этом возможном перемещении. В эту сумму войдет только работа вращающего момента, определенная по формуле:

.

Обобщенную силу получим согласно:

.

Рис. 14.4

Подставим найденные значении (а), (б) и (в) в уравнение Лагранжа:

,

откуда

.

Для определения окружного усилия в точке касание шестерен рассмотрим плоское движение бегающей шестерни. Составим дифференциальное уравнение вращения шестерни вокруг оси ζ, проходящей через центр тя­жести А (рис. 14.4). К шестерне приложены силы: сила тяжести , составляющие реакции кривошипа и и составляющие реакции неподвижной шестер­ни и .

Реакция представляет собой окружное усилие. Направление вращения шестерни примем положитель­ным. Тогда уравнение будет иметь вид

,

откуда

.

Чтобы найти угловое ускорение шестерни , продифференцируем по времени выражение . Получим

,

т.е. . Подставляя это значение в выраже­ние , найдем усилие:

.

Лекция 15

ТЕОРИЯ УДАРА

1 ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА.

ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА

Основное уравнение теории удара. При движении тела под действием обычных сил, рассматривав­шихся до сих пор, скорости точек тела изменяются непрерывно, т. е. каждому бесконечно малому промежутку времени соответствует бесконечно малое приращение скорости. Действительно, если им­пульс любой силы за промежуток времени представить в виде , где — среднее значение этой силы за время , то теорема об изменении количества движения точки, на которую действуют силы , дает

.

Отсюда видно, что когда время бесконечно мало (стремится к нулю), то при обычных силах и приращение скорости будет тоже величиной бесконечно малой (стремящейся к нулю).

Однако если в числе действующих сил будут очень большие силы (порядка 1/τ), то приращение скорости за малый промежуток времени τ окажется величиной конечной.

Явление, при котором скорости точек тела за очень малый (близкий к нулю) промежуток времени τ изменяются на конечную величину, называется ударом. Силы, при действии которых проис­ходит удар, будем называть ударными силами . Промежуток времени τ, в течение которого происходит удар, назовем временем удара.

Так как ударные силы очень велики и за время удара изменяются в значительных пределах, то в теории удара в качестве меры вза­имодействия тел рассматривают не сами ударные силы, а их импульсы. Ударный импульс

является величиной конечной. Импульсы неударных сил за время τ будут величинами очень малыми и ими практически можно пренебречь.

Будем в дальнейшем обозначать скорость точки в начале удара и скорость в конце удара . Тогда теорема об изменении количества движения точки при ударе примет вид

, (15.1)

т. е. изменение количества движения материальной точки за время удара равно сумме действующих на точку ударных импульсов. Урав­нение (15.1) является основным уравнением теории удара и играет в теории удара такую же роль, как основной закон динамики при изучении движений под действием неударных сил.

В заключение отметим, что перемещение точки за время удара будет равно , т. е. величине очень малой, которой практически можно пренебречь.

При действии мгновенной силы перемещение точки приложения силы равно нулю, а скорость точки скачкообразно меняется:

.

В действительности скачок скорости происходит в течение очень малого промежутка времени.

Линией центров назы­вается ось, проходящая че­рез центры тяжести соуда­ряющихся тел.

Удар называется цен­тральным, если точка К со­прикосновения соударяю­щихся тел лежит на линии центров , а касательная плоскость, проведенная в точке соприкосновения к поверхностям этих тел, перпендикулярна к линии центров (рис. 15.1).

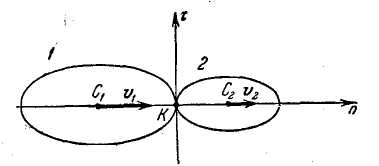
Рис. 15. 1 Рис. 15.2

Удар называется прямим, если скорости центров тяжести соуда­ряющихся тел в начале удара лежат на линии центров (рис. 15.2).

Если хотя бы одна из ско­ростей центров тяжести соуда­ряющихся тел в начале удара не лежит на линии центров, то удар называется косым (рис. 15.3).

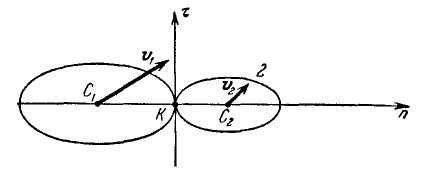
Рис. 15.3

Рассмотрение процесса уда­ра по существу требует выхода за рамки классической меха­ники — отказа от схемы абсо­лютно твердого тела и перехода к схеме деформируемого тела. В зависимости от степени вос­становлений недеформированного состояния удары разделяются на неупругие, частично упру­гие и упругие.

Удар называется неупругим, если недеформированное состояние со­ударяющихся тел не вос­станавливается. В конце удара центры тяжести тел движутся с одинаковыми скоростями.

Удар называется частично упругим, если недеформированное со­стояние не полностью восстанавливается. В конце удара центры тяжес­ти тел движутся с разными скоростями.

Удар называется упругим, если недеформированное состояние соударяющихся тел полностью восстанавливается.

Итак, из всех полученных результатов вытекает следующее:

1) действием неударных сил (таких, например, как сила тяже­сти) за время удара можно пренебречь;

2) перемещениями точек тела за время удара можно пренебречь и считать тело во время удара неподвижным;

3) изменения скоростей точек тела за время удара определяются основным уравнением теории удара (1).

Общие теоремы теории удара. Рассмотрим, какой вид принимают общие теоремы динамики для системы материальных тачек при ударе.

1. Теорема об изменении количества дви­жения системы при ударе. Уравнение об изменении количества движения системы, сохраняет свой вид и для случая удара. Но так как импуль­сами обычных сил при ударе пренебрегают, то в правой части оста­нутся только ударные импульсы. Следовательно, при ударе

, (15.2)

т. е. изменение количества движения системы за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на систему.

В проекциях на любую координатную ось уравнение (15.2)

(15.3)

Эти уравнения показывают, что изменение проекции количества дви­жения системы на любую ось равно сумме проекций на ту же ось всех внешних ударных импульсов, приложенных к системе.

Если геометрическая сумма всех внешних; ударных импульсов равна нулю, то, как видно из уравнения (15.2), количество дви­жения системы за время удара не изменяется. Следовательно, внут­ренние ударные импульсы не могут изменить количества движения всей системы.

2. Теорема об изменении главного момен­та количеств движения системы (теорема моментов) при ударе. Теорема моментов принимает для случая удара вид, несколько отличный от полученного ранее; объясняется это тем, что точки системы за время удара не переме­щаются. Рассмотрим систему, состоящую из п материальных точек. Обозначим равнодействующую внешних ударных импульсов, дей­ствующих на точку с массой , через , тогда после соответствующих преобразований получим

, (15.4)

т. е. изменение кинетического (главного) момента механической системы относительно любого неподвижного центра при ударе равно геометрической сумме моментов всех внешних ударных импульсов, приложенных к точкам системы, относительно того же центра.

В проекциях на любую ось равенство (15.4) дает

. (15.5)

т. е. изменение кинетического момента механической системы относи­тельно любой оси при ударе равно сумме моментов всех внешних ударных импульсов, приложенных к точкам системы относительно той же оси.

Из полученных уравнений следует, что если сумма моментов внешних ударных импульсов относительно какого-нибудь центра (или оси) равна нулю, то главный момент количеств движения системы относительно этого центра (или оси) за время удара не изменяется. Следовательно, внутренние ударные импульсы не могут изменить главный момент количеств движения системы.