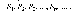44. Необходимое условие локального экстремума функций нескольких переменных.

Теорема. Пусть функция f(x₁, ..., x_m) определена в некоторой окрестности т. 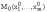, дифференцируема в точке М₀, и имеет в этой точке локальный экстремум, тогда все частные производные первого порядка функции f в т. М₀ равны нулю:

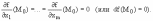
45. Достаточное условие локального экстремума функций нескольких переменных.

Пусть в некоторой окрестности стационарной точки определены частные производные второго порядка функции f(x₁, ..., x_m), которые являются непрерывными в т. М₀. Если в этой точке второй дифференциал d² f(M₀) является знакоопределенной квадратичной формой от dx₁, ..., dx_m, то в т. М₀ функция имеет локальный экстремум (локальный максимум, если d² f(M₀) отрицательно определена, и локальный минимум, если d² f(M₀) положительно определена), если же d² f(M₀) знакопеременна, то в т. М₀ экстремума нет.

Пусть (x₀; y₀) –стац т. В окр-ти этой т. сущест непрер част произ 2ого порядка, тогда, если 1) Δ= lf’’_xx f’’_xy f’’_yx f’’_yy l >0, то т. (x₀; y₀) - экстремум. При этом, если f’’_xx(x₀; y₀) >0, то (x₀; y₀) -т. лок, мин, и наоборот.

46. Условный экстремум.

g1(x1..xn)=0 и gs(x1…xn)=0 – урние связи.

Задают область X. Опр: X⁰(вектор) – условный лок мах/min ф-ции f(x(вектор)), если для любого X(вектор) сушест Oε(X (вектор)⁰) пересек X то вып f(x⁰(вектор))>=f (x(вектор)) и наоборот.

Общее название для условных минимумов и максимумов — условные экстремумы.

47. Метод Лагранжа.

Пусть функции f и g₁ …g_s определены и имеют непрерывные ча­стные производные в окрестности точки х* причем, векторы

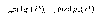
линейно независимы. Тогда если х* - точка условного экстремума функции f при условиях

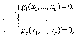
то найдутся числа ʎ₁ …ʎ_s для ко­торых x* - стационарная точка функции

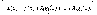(на лекции они вычитаются!!!)

Ф-ция L называется ф-цией Лагранжа, а числа множителями Лагранжа.

48. Наибольшее и наименьшее значения непрерывной функции на замкнутом ограниченном множестве.

Множество S называется ограниченным, если оно содержится внутри круга (для множества на плоскости) или внутри шара (для множества в пространстве), имеющего достаточно большой радиус. Множество называется замкнутым, если оно включает в себя все свои предельные точки.

Пусть z= f(x,у) — непрерывная функция, a S — замкнутое и огра­ниченное множество, лежащее в области определения функции f. Тогда в S существуют точки, в которых функция принимает свои наиболь­шее и наименьшее значения, множество значений представляет собою отрезок [f_наим,f_наиб].

49. Кратные интегралы и их свойства. Условия интегрируемости функции.

Определение. Если существует конечный предел интегральных сумм при ʎ->0 то функция f(x;y) называется интегрируемой в области D. Значение этого предела называется двойным интегра­лом по области D X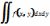

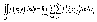
свойства двойного интеграла.

1. Если функция f(x;y) интегрируема в области D, то для любого числа к функция kf(x;y) также интегрируема в D и

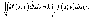
2. Если функции f(x;y) и g(x;y) интегрируемы в области D, то их алгебраическая сумма также интегрируема в этой области и

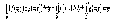
3. Если функции f(x;y) и g(x;y) интегрируемы в области D и f(x; у) <= g(x; у) во всех точках D, то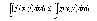

4. Если функция f(x;y) ограничена на множестве Г нулевой площади, то

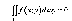
5. Свойство аддитивности интеграла. Если область интегрирова­ния D может быть разбита на две части D₁ и D₂, не имеющих общих внутренних точек, так, что D=D₁ объединение D₂, и f(x;y) интегрируема в D₁ и D₂, то в области D эта функция также интегрируема, и

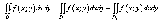6. Теорема о среднем. Если функция f(x;y) непрерывна в области D, то в этой области найдется такая точка (о, т ), что

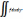
Если функция f(x, у) определена и непрерывна в прямоугольнике Р = {a=<х=<b, с=<у=<d), то существует двойной интеграл P 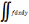Пусть G — ограниченная область, f— ограничен­ная функция на G,Г — объединение границы G и множества точек разрыва f на G. Предположим, что площадь Г равна нулю. Тогда существует интеграл G

50. Сведение кратного интеграла к повторному интегралу.

Если функция f(x,y) интегрируема в области G и при любом фиксированном х из [а,b] существует интеграл 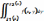справедлива формула

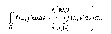
51. Формула замены переменных в двойном интеграле. Использование полярных координат для вычисления двойных интегралов.

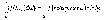
В полярных координатах :

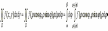
52. Геометрические приложения двойных интегралов: вычисление площадей плоских фигур и объемов пространственных тел.

Определение. Если существует конечный предел интегральных сумм при ʎ->0 то функция f(x;y) называется интегрируемой в области D. Значение этого предела называется двойным интегра­лом по области D

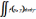
53. Несобственные кратные интегралы. Интеграл Эйлера-Пуассона.

Пусть GсR² — неограниченное множество, f(x, у) - функция, интегрируемая по всякому подмножеству в G вида G∩D, где D - ограниченное множество с границей нулевой площади. Если для любого допустимого семейства {D_t} предел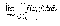 существует и не зависит от выбора семейства {D_t}, то данный

предел обозначается G и называется несобственным двойным интегралом от f по G.

54. Числовые ряды.

Определение. Пусть дана числовая последовательность а₁ ,а₂, а₃….a_n . Выражение вида

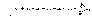
называют числовым рядом, или просто рядом.

Числа а₁ ,а₂, а₃,….a_n называют членами ряда, число а_п с общим номером п называют общим членом ряда.

Суммы конечного числа первых членов ряда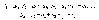

называют частичными суммами ряда. Так как число членов ряда бесконечно, то частичные суммы образуют числовую последовательность