- •1.5. Дифференциальное исчисление Для замечаний
- •1.5.15. Исследование поведения функций с помощью производных.
- •1.5.15.1. Условие постоянства функций.
- •1.5.15.2. Признак монотонности функции
- •1.5.15.3. Экстремум дифференцируемой функции
- •1.5.15.4. Экстремум функции, недифференцируемой в данной точке
- •1.5.15.5. Направление выпуклости графика функции
- •1.5.15.6. Точки перегиба графика функции
- •1.5.15.7. Теоремы о достаточных условиях перегиба графика функции
- •1.5.15.8. Асимптоты графика функции
- •1.5.15.9. Примеры построения графиков функций
1.5.15.7. Теоремы о достаточных условиях перегиба графика функции
Теорема 1. (первое достаточное условие перегиба).
Пусть функция f(x)
1) имеет вторую производную в некоторой окрестности точки С;
2)
![]() ,
тогда, если существует окрестность, в
пределах которой вторая производная
,
тогда, если существует окрестность, в
пределах которой вторая производная
![]() имеет разные знаки слева и справа от
точки C, то график этой функции имеет
перегиб в точке М(с,f(с)).
имеет разные знаки слева и справа от
точки C, то график этой функции имеет
перегиб в точке М(с,f(с)).
Замечание 1.
Сформулируем обобщение теоремы 1. При
определении точки перегиба будем
считать, что касательная к графику
функции в рассматриваемой точке может
быть параллельной оси 0y (т.е.![]() ).
).
Пусть функция
f(x): 1) имеет конечную вторую производную
всюду в некоторой окрестности точки С,
за исключением, быть может, самой точки
С; 2) функция f(x) непрерывна в точке С; 3)
график функции имеет касательную в
точке М(с,f(с)) (может быть и параллельно
оси 0y). Тогда, если существует окрестность
точки С, в пределах которой
![]() имеет разные знаки слева и справа от
точки С, то график функции y=f(x) имеет
перегиб в точке М(с,f(с)).
имеет разные знаки слева и справа от
точки С, то график функции y=f(x) имеет
перегиб в точке М(с,f(с)).
Замечание 2.
|
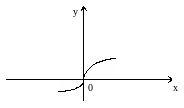
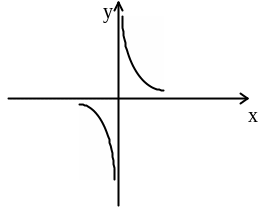
Пункт 2 в условии теоремы исключает случай, приведенный на рис. 1, а пункт 3 - на рис. 2 (слева от точки С график функции касается прямой х=С в точке М, а справа касания нет) |
Пример.
Найти точки перегиба графика функции
![]() .
.
Рис. 3 |
Так как
|
Отсюда следует, что точка (0,0) является точкой перегиба; слева от этой точки график функции имеет выпуклость вниз, а справа вверх.
1.5.15.8. Асимптоты графика функции
Определение 1.
Прямая х=а
называется вертикальной асимптотой
графика функции y=f(x), если хотя бы одно
из предельных значений
![]() равно
или .
равно
или .
Рис. 1 |
Пример.
|
Определение 2. Пусть функция y=f(x) определена для всех x>a (x<a). Прямая Y=kx+b называется наклонной асимптотой графика функции y=f(x) при х (х ), если функция f(x) представима в виде
![]() .
.
Теорема. Для того, чтобы график функции y=f(x) имел при х
(х ) наклонную асимптоту, необходимо и достаточно, чтобы существовали два предела:
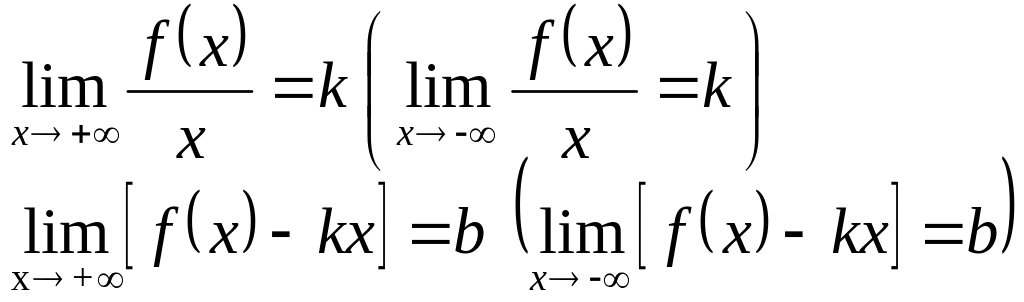 .
.
Доказательство.
Необходимость.
Пусть график функции y=f(x) имеет асимптоту,
для определенности, при х
,
т.е. f(x) может
быть представлена в виде
![]()
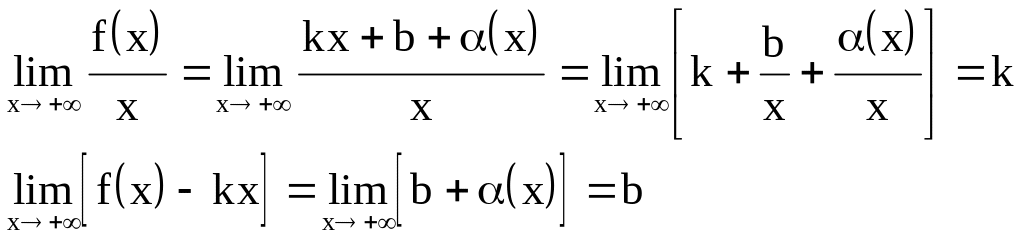
Достаточность.
Пусть
существует
![]() ,
тогда f(x)kx=b+(x)
и
,
тогда f(x)kx=b+(x)
и
![]() .
Отсюда следует, что f(x)=kx+b+(x),
где (x)
- бесконечно малая функция при х
.
.
Отсюда следует, что f(x)=kx+b+(x),
где (x)
- бесконечно малая функция при х
.
Замечание. Расположение графика относительно асимптоты при больших х определяется знаком разности =f(x)kxb
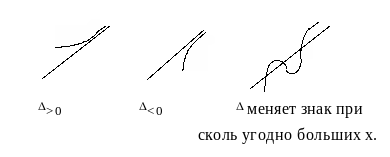
При х аналогично

Расположение графика относительно вертикальных и наклонных асимптот позволяет проверить исследование функции на экстремум, а также на направление выпуклости графика.

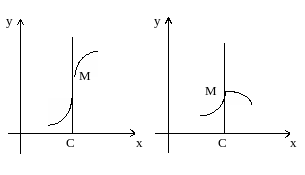 Рис. 1
Рис. 2
Рис. 1
Рис. 2