Тема 6. Движение твердого тела вокруг неподвижной точки. (сферическое движение)

Д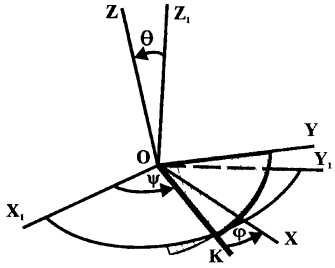 вижение твердого тела, имеющего неподвижную точку, называют вращением твердого тела вокруг неподвижной точки. Это движение также называют сферическим, поскольку траекториями всех точек тела являются сферы, центр которых находится в неподвижной точке. Для задания движения твердого тела, имеющего одну неподвижную точку, используют углы Эйлера (рис. 1).

Т

Рисунок 1

очка — начало подвижной и неподвижной систем координат. — неподвижная система координат; — подвижная система координат, связанная с твердым телом; — линия узлов (линия пересечения неподвижной плоскости и подвижной ); — угол процессии (угол между осью и линией узлов); — угол собственного вращения (угол между линией узлов и подвижной осью ОХ); — угол нутации (угол между неподвижной осью и подвижной осью ). Все углы откладываются в направлении против хода часовой стрелки от осей , и линии узлов .

Положение тела в любой момент времени определяется углами Эйлера (прецессии, собственного вращения и нутации), которые должны быть однозначными функциями времени:

уравнения или закон вращения твердого тела вокруг неподвижной точки.

(1)

Угловая скорость

П

Рисунок 2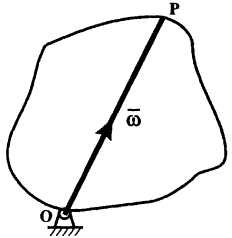

о теореме Эйлера—Даламбера всякое перемещение твердого тела, имеющего одну неподвижную точку, можно заменить поворотом вокруг оси , проходящей через эту точку (рис. 2). Ось будет мгновенной осью вращения, на которой все точки имеют скорость, равную нулю. Вектор угловой скорости будет направлен по мгновенной оси вращения в сторону, откуда виден поворот тела против хода часовой стрелки. Модуль вектора угловой скорости равен: (2)

Вектор угловой скорости в отличие от вращательного движения вокруг неподвижной оси может изменяться по величине и направлению.

Угловое ускорение

Угловое ускорение — производная вектора угловой скорости по времени:

. (3)

В

Рисунок 3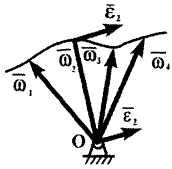

ектор углового ускорения, как производная вектора по скалярному аргументу, направлен по касательной к годографу вектора угловой скорости, который изменяется по величине и направлению (рис. 3). Поэтому вектор углового ускорения в общем случае не направлен по мгновенной оси вращения, как вектор угловой скорости. Вектор углового ускорения изображают в неподвижной точке параллельно касательной к годографу вектора угловой скорости (рис. 3).

Скорость точки

Скорости точек твердого тела в сферическом движении определяют по формуле Эйлера (рис. 4): (4)

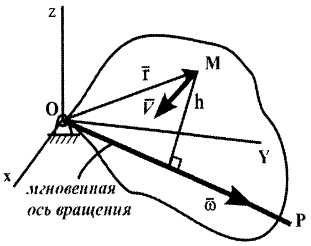г де — вектор угловой скорости; — радиус-вектор данной точки относительно неподвижной точки. Модуль скорости равен:

(5)

г

Рисунок 4

де — кратчайшее расстояние точки до мгновенной оси вращения.

Направление вектора скорости определяется направлением векторного произведения , т. е. вектор скорости будет направлен перпендикулярно плоскости векторов и , откуда поворот вектора к вектору виден на наименьший угол против хода часовой стрелки (рис. 4).

Ускорение точки

Д ифференцируем формулу (4) по времени

(6),

г

Рисунок 5

де — ускорение точки; — угловое ускорение тела; — скорость точки. Тогда (7)

Слагаемое представляет собой вектор вращательного ускорения точки, величина которого равна: , где — расстояние от точки до вектора . Вектор направлен в соответствии с направлением векторного произведения (рис. 5)

Слагаемое — вектор осестремительного ускорения, который направлен в соответствии с векторным произведением, т. е. по направлению перпендикуляра , опущенного из точки на мгновенную ось вращения. Величина осестремительного ускорения равна:

(8)

Ускорение точки в сферическом движении равно геометрической сумме вращательного и осестремительного ускорений:

(9)

Так как вращательное и осестремительное ускорения не перпендикулярны друг другу, то величина ускорения точки равна:

. (10)