2. Знакопеременные ряды

Пример 14. Исследовать на сходимость ряд

(плюс, два минуса, три плюса, четыре минуса, пять плюсов и т. д.; ).

Решение. Составим ряд из модулей членов данного ряда . Он сходится как обобщенный гармонический ряд с показателем . Следовательно, сходится и данный ряд, и притом абсолютно.

Пример 15. С помощью признака Лейбница исследовать на сходимость знакочередующийся ряд , выяснить характер сходимости.

Решение. Так как (члены ряда монотонно убывают) и так как , то, по признаку Лейбница, данный ряд сходится. Однако он сходится лишь условно, так как ряд, составленный из модулей его членов, расходится (он является гармоничеслим).

Пример 16. Показать, что если изменить порядок следования членов условно сходящегося ряда Лейбница так, чтобы за каждым его положительным членом следовало два отрицательных, то получится ряд

, (А)

сумма которого будет в два раза меньше, чем у исходного ряда.

Решение. Условная сходимость данного ряда доказана в примере 15. Обозначим его сумму через , т. е. положим

.(Б)

Преобразуем теперь ряд (А) следующим образом:

.

Как видно, сумма ряда (А), полученного простой перестановкой членов ряда, в два раза меньше суммы исходного ряда Лейбница.

Заметим, что , так как

ввиду положительности разностей чисел, стоящих внутри каждой пары скобок.

Пример 16. Исследовать на сходимость ряд .

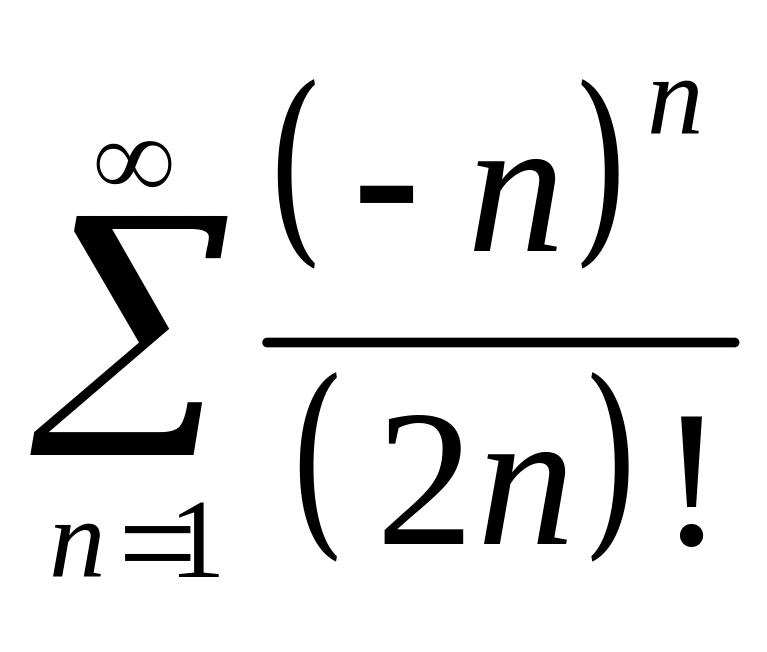Решение. Исследуем данный знакочередующийся ряд сразу на абсолютную сходимость. С этой целью составим ряд из модулей членов данного ряда: . Применим к этому ряду признак Даламбера:

.

Ряд из модулей сходится. Следовательно, исходный ряд сходится абсолютно.

Пример 17. Исследовать на сходимость ряд

(два плюса, два минуса и т.д.)

Решение. Из модулей членов данного ряда составим ряд

Он сходится, так как его частичная сумма монотонно возрастает с возрастанием n и является ограниченной, например, числом . Следовательно, данный ряд сходится абсолютно.

Пример 17. Исследовать на сходимость ряд .

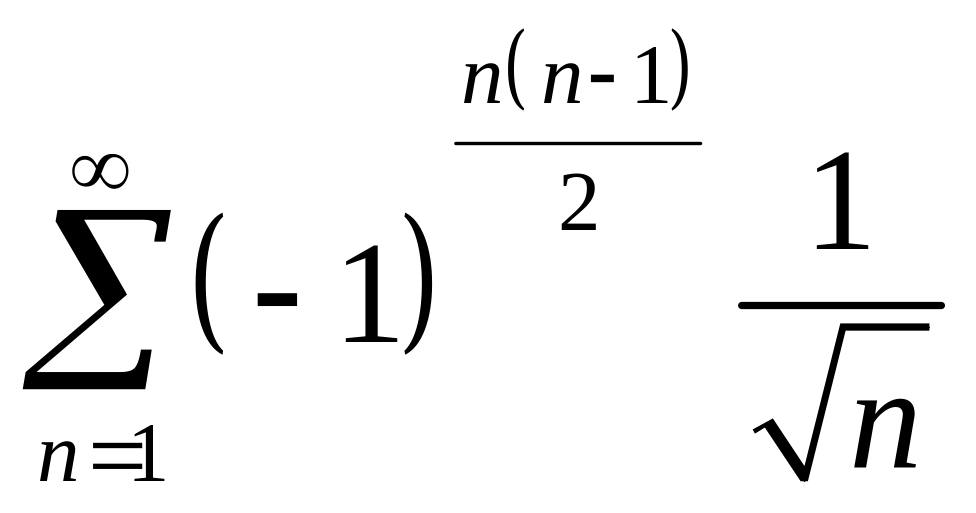Решение. Данный ряд

является знакопеременным, и если сходится, то лишь условно, так как ряд, составленный из модулей его членов, расходится как обобщенный гармонический с показателем . Из данного ряда попарной группировкой его членов образуем ряд

.

Он сходится по признаку Лейбница.

Пусть сумма этого ряда равна , то есть частичные суммы

имеют предел, равный . Тогда и частичные суммы исходного ряда 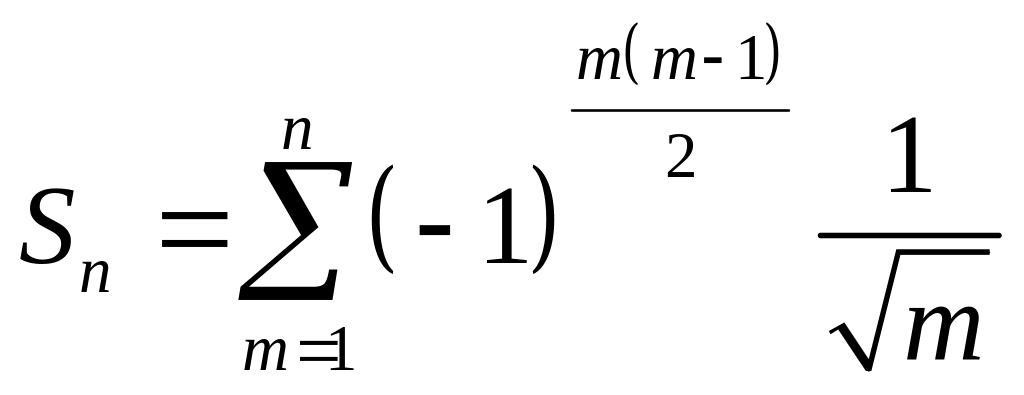имеют предел, равный , и, следовательно, исходный ряд сходится условно.

В самом деле

,

а . Отсюда следует, что .

Рассмотрим теперь примеры на применение признаков Абеля и Дирихле.

Пример 18. Исследовать на сходимость ряд .

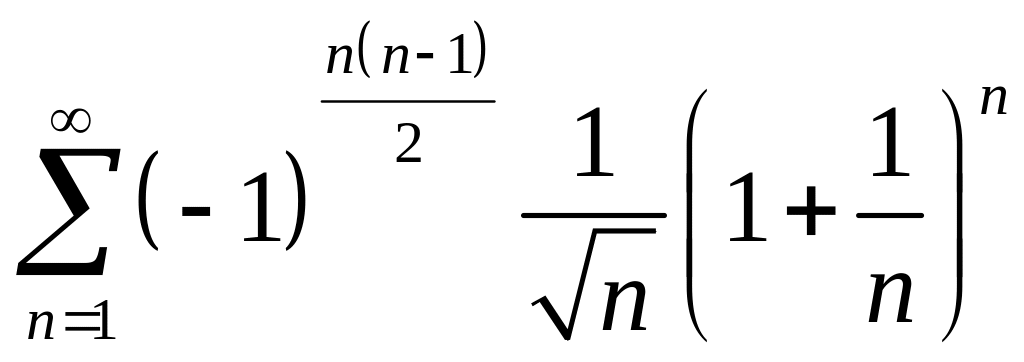Решение. Ряд, составленный из модулей членов данного ряда, расходится, так как

при , а ряд расходится как обобщенный гармонический с показателем . Следовательно, речь может идти только об условной сходимости данного ряда. Признак Лейбница здесь неприменим, так как ряд не является знакочередующимся. Применим признак Абеля. Пусть

.

Ряд сходится (см. пример 17), а последовательность монотонна и ограничена , поэтому данный ряд, по признаку Абеля, сходится (и притом лишь условно).

Пример 19. Исследовать сходимость ряда .

Решение. Простейшая оценка не дает информации о поведении ряда . Покажем, что данный ряд сходится. Положим и . Последовательность монотонно стремится в нулю при . Докажем, что частичные суммы ряда ограничены.

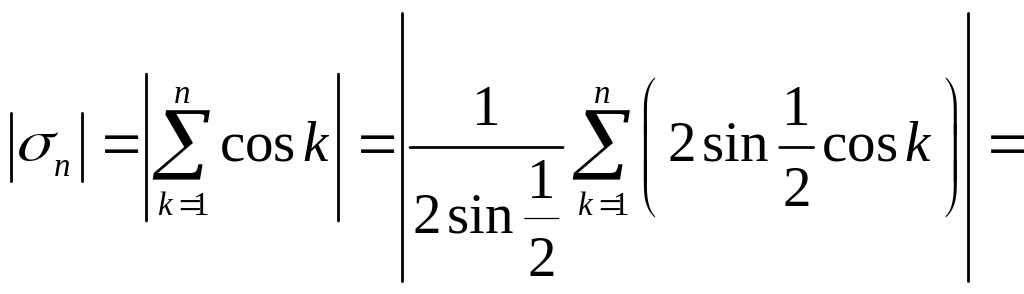
(А)

В силу признака Дирихле данный ряд сходится. Для исследования абсолютной сходимости этого ряда удобно воспользоваться оценкой . Имеем: . Ряд расходится, а ряд также, как и исходный ряд, сходится в силу признака Дирихле (оценка 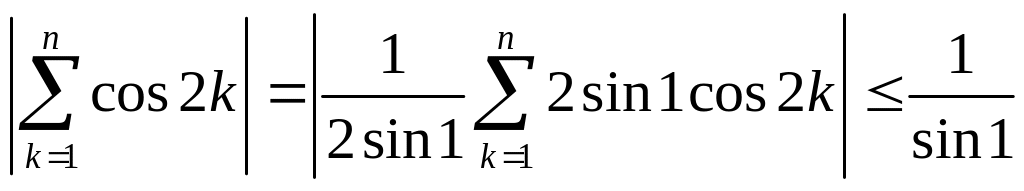проводится аналогично (А)). Следовательно, расходится ряд , а в силу теоремы сравнения и ряд . Итак, ряд сходится условно.