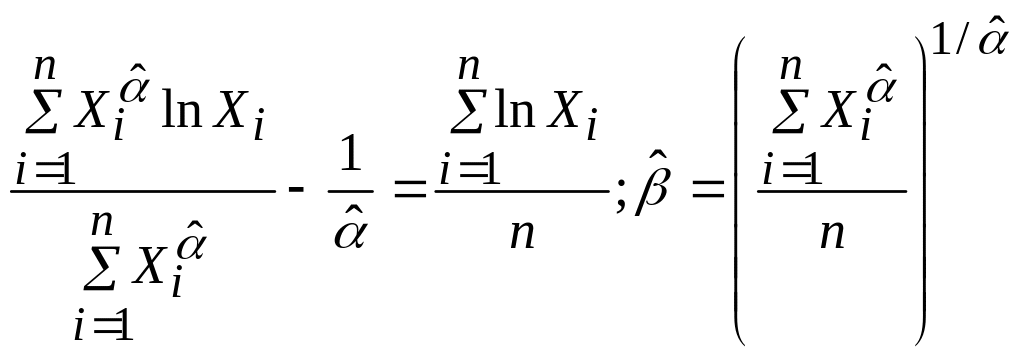5. Распределение Вейбулла

Функцию распределения Вейбулла легко обратить, чтобы найти

что ведет к получению следующего алгоритма обратного преобразования.

1. Генерируем .

2. Возвращаем .

Мы снова используем тот факт, что U и 1-U имеют одно и то же распределение U(0,1), поэтому на шаге 2 можно заменить на , если нужен буквальный метод обратного преобразования. Этот алгоритм можно также обосновать, отметив, что если Y имеет экспоненциальное распределение со средним то .

Распределение Вейбулла
Варианты распределений	Время выполнения какой – либо задачи, время безотказной работы устройства.
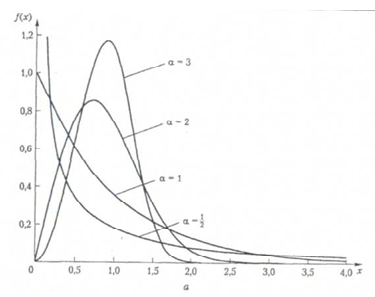
Плотность (рис.1.4.)
Распределение
Параметры	параметр формы , масштабный параметр
Область
Среднее
Дисперсия
Мода
Оценка максимального правдоподобия	Должны выполняться два следующих равенства: Первое равенство может быть численно решено для с помощью метода Ньютона, а второе непосредственно даёт Общий рекурсивный шаг для итераций Ньютона где (Эти формулы, а также доверительный интервал Для истинных и см. в работе Томана, Бейна и Антля. В качестве отправной точки для этих. Итераций может использоваться оценка [Menon,1963;Thoman, Bain and Antle, 1969]. В работе Томана, Бейна, Антля [Thoman, Bain and Antle, 1969] сообщалось, что при таком выборе с точностью до четырёх разрядов требовалось. Среднее только 3,5 итераций Ньютона.
Примечания	1.Распределение и одинаковы. 2.Тогда и только тогда , когда . 3.Логарифм (натуральный) случайной величины с распределением Вейбулла имеет распределение известное как распределение экстремального значения или распределения Гумбеля. 4.Распределение также называется распределением Рэлея с параметром и обозначается как Если Y и Z – независимые нормально распределённые величины со средним значением 0 и дисперсией , тогда 5.При распределение Вейбулла становится вырожденным в точке . Следовательно, плотности распределений Вейбулла для больших значений имеют резкий подъём в моде. 6.Распределение Вейбулла имеет отрицательную асимметрию, когда . 7.
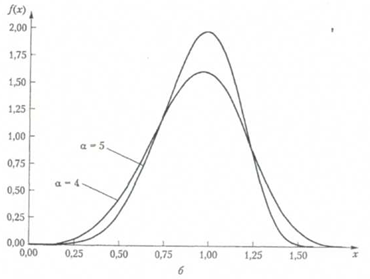
Рис.1.4. Функции плотностей распределения вероятностей а – положительная асимметрия; б – отрицательная асимметрия

6. Нормальное распределение

Прежде всего, обратите внимание, что при можно получить , задав поэтому мы можем ограничиться генерированием стандартных нормально распределенных случайных величин. В этой ситуации очень большое значение имеет эффективность алгоритма, поскольку плотность нормального распределения часто применяется для определения оцениваемой сверху функции в методе принятия-отклонения при генерировании случайных величин из других распределений. Нормально распределенные случайные величины также можно прямо преобразовать в случайные величины, которые можно получить из других распределений, например логнормального. Кроме того, специалистам по статистике, стремящимся эмпирически оценить при изучении по методу Монте-Карло распределение, соответствующее нулевой гипотезе статистической проверки на нормальность, понадобится эффективный источник нормальных случайных величин.

Сегодня все еще применяется один из ранних методов генерирования случайных величин с распределением N(0,1), представленный Боксом и Мюллером [Box and Mullcr, 1958], несмотря на наличие гораздо более быстро работающих алгоритмов. Однако у него есть то преимущество, что в нем сохраняется однозначное соответствие между примененными случайными числами и полученными случайными величинами с распределением N(0, 1); это может оказаться полезным для поддержания синхронизации при использовании общих случайных чисел или несовместных величин для уменьшения дисперсии.

Согласно этому методу нужно просто:

1. Генерировать независимые и одинаково распределенные величины и с распределением U(0, 1),

2. Определить и . Тогда и будут независимыми и одинаково распределенными случайными величинами с распределением N(0,1).

Поскольку мы получили пары случайных искомых величин, можем вызвать подпрограммы с нечетным номером, вычислить и так, как только что было описано, но вернуть только , сохранив для немедленного возвращения при следующем (четном) вызове. Таким образом, мы используем два случайных числа для получения двух случайных величин с распределением N(0,1). В принципе такой метод действителен, если , и являются действительно независимыми и одинаково распределенными случайными величинами с распределением U(0,1), однако могут возникнуть сложности, если на практике окажется, что и являются фактически смежными случайными числами, полученными с помощью линейного конгруэнтного генератора. В связи с тем, что будет зависеть от из-за рекурсии в уравнении, можно утверждать, что сгенерированные величины и попадут на спираль в пространстве , вместо того чтобы представлять действительно независимое нормальное распределение [Bratley, Fox and Schrage, 1987, p. 223-224]. Из этого следует, что метод Бокса и Мюллера не должен использоваться с одним потоком линейного конгруэнтного генератора, взамен этого можно было бы применять отдельные потоки сложного генератора.

Усовершенствованный метод Бокса и Маллера, в котором упразднены тригонометрические вычисления, был описан Марсальи и Бреем и стал известен как метод полярных координат. Метод основывается на специальном свойстве нормального распределения. Метод полярных координат, при котором случайные величины с распределением N(0,1) также генерируются парами, имеет следующий вид.

1. Генерируем и как независимые и одинаково распределенные случайные величины с распределением U(0, 1); пусть для и пусть

2. В случае, если , возвращаемся к шагу 1, иначе пусть . Тогда и являются независимыми и одинаково распределенными случайными величинами с распределением N(0,1).

Поскольку «отклонение» значений и может произойти на шаге 2 (с вероятностью ), для метода полярных координат требуется случайное количество случайных величин с распределением U(0,1), чтобы генерировать каждую пару случайных величин с распределением N(0,1).

Нормальное распределение
Варианты распределений	Ошибки различного типа, например точка попадания бомбы; величины, представляющие собой сумму большого кол-ва других величин (на основании центральной предельной теоремы)
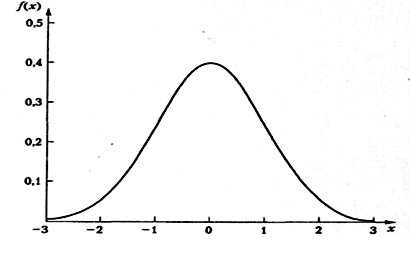
Плотность (рис.1.5.)	для всех вещественных чисел x
Распределение	Конечная форма отсутствует
Параметры	Параметр положения , масштабный параметр
Область
Среднее
Дисперсия
Мода
Оценка максимального правдоподобия
Примечания	1. Если две совместно нормально распределенные случайные величины являются некоррелированными, они также являются независимыми. К распределениям, отличным от нуля этот вывод не относится. 2. Предположим, что имеют совместное многомерное нормальное распределение. Пусть и Тогда для любых вещественных чисел случайная величина имеет нормальное распределение со средним и дисперсией . Заметьте, нам не требуется допускать независимость величин . Если величины являются независимыми, . 3. Распределение N(0,1) называется стандартным или единичным нормальным распределением. 4. Если - независимые случайные величины, имеющие стандартное нормальное распределение, величины, имеют распределение «хи-квадрат» с k степенями свободы, которое также является gamma-распределением (k/2,2). 5. Если имеет логнормальное распределение с параметрами и , обозначаемое как . 6. Если , Y имеет распределение «хи-квадрат» с k степенями свободы, а X и Y – независимые величины, то имеет t – распределение с k степенями свободы (иногда именуемое распределением Стьюдента). 7. Если нормальное распределение используется, чтобы представить неотрицательную величину (скажем время), его плотность должна быть усечена в точке x=0. 8. При нормальное расределение становится вырожденным в точке .
Рис.1.5. Функция плотности распределения вероятностей N(0,1)