Корреляционное отношение

Коэффициент корреляции является надежной мерой линейной связи. В более же общем случае для доказательства наличия как линейной, так и нелинейной связи используется корреляционное отношение.

Оценкой корреляционного отношения  называется отношение выборочных дисперсий групповых средних или к выборочным оценкам общих дисперсий и исследу-емых величин. Таких отношений в двумерном распределении может быть, как и уравнений регрессии, два, т.е. _v/u и _u/v:

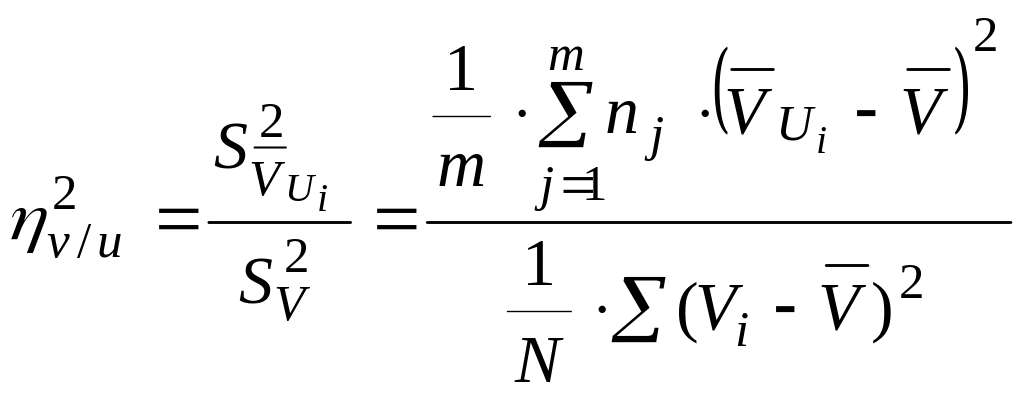и ,

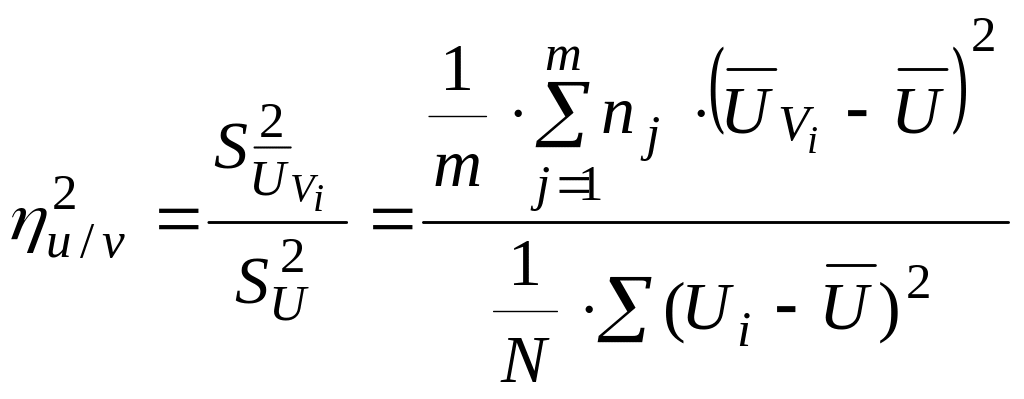где и - условные дисперсии групповых средних, и - условные групповые средние для j-го класса, п_j – число наблюдений в j-м классе, т – число классов, U_i и V_i – исходные наблюдения величин U и V, N – объем выборки.

Условные групповые средние и условные дисперсии групповых средних рассчитываются по формулам:

, , , .

Однако эти формулы удобны только для понимания сути корреляционного отношения, но не для вычислений. Для практических же расчетов используются следующие формулы:

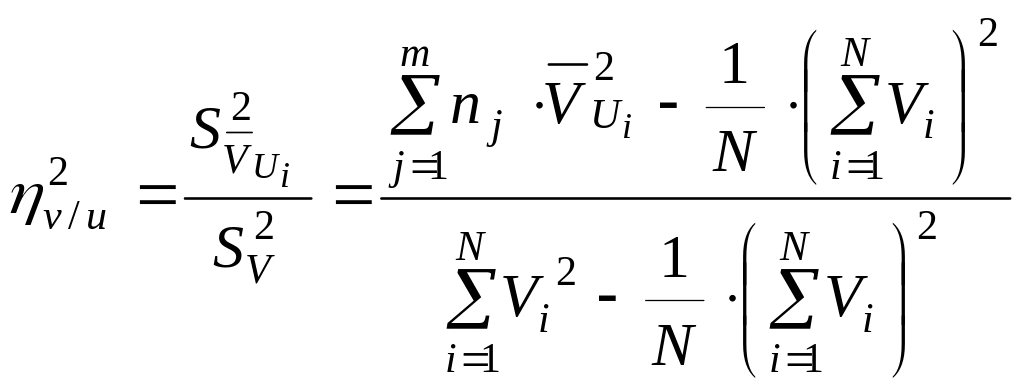и .

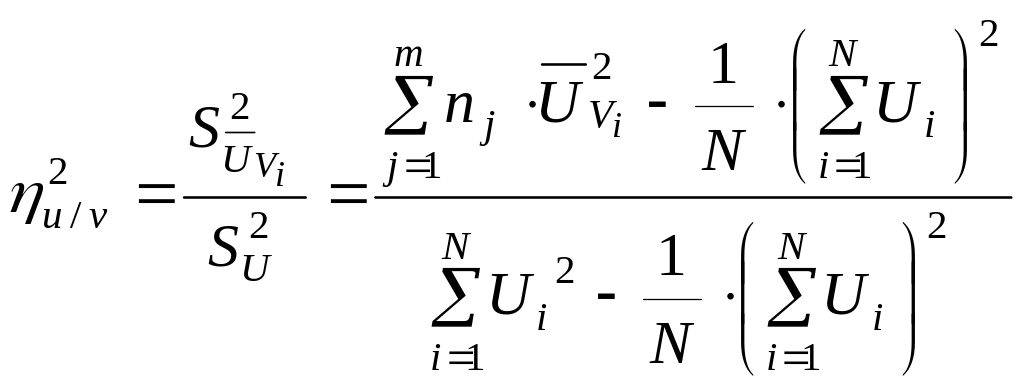Для расчета корреляционных отношений исходные данные предварительно группируют в классы по значениям величины, принимаемой за аргумент. Если исследуется отношение _v/u, то группируется величина V по классам значений U, а при расчетах _u/v группируются значения U по классам величины V.

При расчетах по методу замены переменных используются следующие формулы:

; ; .

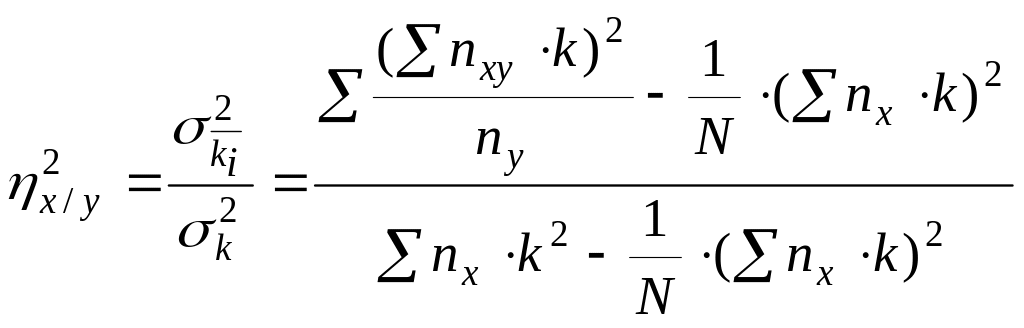Свойства корреляционного отношения:

1. корреляционное отношение всегда положительно и изменяется от 0 до +1, т.е. 0+1;

2. чем теснее связь, тем больше ;

3. при =0 связь отсутствует, при =1 связь функциональная;

4. всегда >  r ;

5. при  =  r  связь линейная, т.е. расхождение между  и  r  может служить критерием кри-волинейности связи;

6. при =  r  =1 связь линейная функциональная.

Оценка значимости корреляционного отношения  проводится двумя способами:

1. с помощью критерия  по формуле: 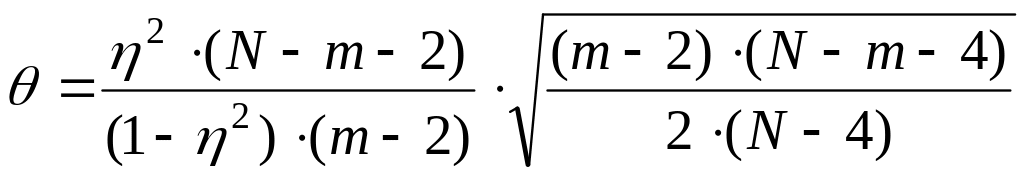, где т – число классов, N – объем выборки.

_расч. сравнивается с _теор. для принятого уровня значимости  по таблицам функции нормального распределения. Например, для =0,05 _теор.=1,96. Если _расч. > _теор., то нулевая гипотеза об отсутствии корреляционной связи отвергается и связь считается значимой.

2. с помощью среднеквадратической погрешности оценки корреляционного отношения по формулам: при N 5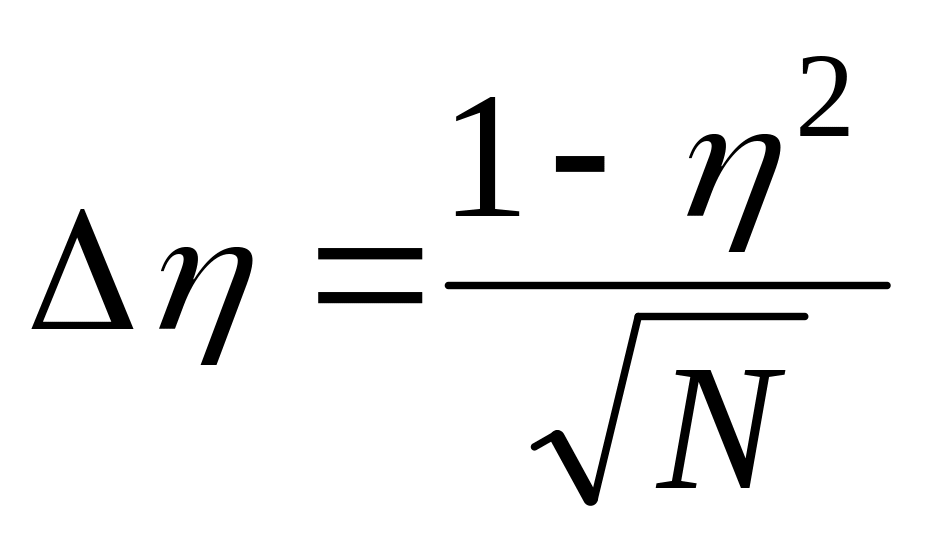0 ; при N<50 .

Корреляционная связь считается значимой, если  t, где t – коэффициент вероятно-сти для принятого уровня значимости . Так, для =0,05 t=2, а для =0,01 t=3.

Проверка гипотезы о линейности связи проводится двумя способами:

1. по равенству =  r  ;

2. с помощью критерия Фишера: . Рассчитанное значение критерия F_расч. сравнивается с теоретическим F_теор. для принятого уровня значимости  и степеней свободы f₁ = т - 2 и f₂ = N – т. Если F_расч. > F_теор., то нулевая гипотеза о нелинейности корреляционной связи отвергается и связь считается линейной.

Регрессионный анализ

Регрессионным анализом называется метод выявления зависимости одной переменной V, принятой за функцию, от набора значений другой переменной U, принятой за аргумент.

В геологии регрессионный анализ применяется также очень широко, например:

1. при разведке полезных ископаемых – для оценки в рудах содержаний попутных компонентов по основным, для определения содержаний полезных компонентов по замерам физических свойств руд (магнитной восприимчивости, электрического сопротивления, гамма-излучения), для определения объемной массы руд по содержанию полезного компонента и т.д.;

2. при разработке месторождений – для уточнения параметров рудных тел в неотработанных блоках по результатам сопоставления данных разведки и эксплуатации отработанных блоков или по данным геофизических методов опробования;

3. при геохимических поисках по первичным ореолам рассеяния;

4. при фациально-формационном анализе магматических комплексов;

5. при комплексной интерпретации геофизических данных и т.д.

Основными задачами и одновременно этапами регрессионного анализа являются:

1. установление формы зависимости V от U, т.е. типа уравнения V=f(U) (линейная или нелинейная);

2. расчет коэффициентов регрессии выбранного типа уравнения;

3. оценка достоверности полученного уравнения.

Выбор типа уравнения (формы зависимости) производится в процессе анализа корреля-ционного графика и построения эмпирической линии регрессии. При этом учитывается характер выявленной связи (прямая или обратная), ее вид (линейная или нелинейная) и теснота.

Линейная зависимость выражается уравнениями вида V= а_v/u + b_v/u  U и U= а_u/v + b_u/v  V, которые называются уравнениями простой средней квадратической регрессии, а коэффициенты а_v/u , b_v/u , а_u/v , b_u/v – коэффициентами регрессии. Системе из двух случайных величин U и V всегда соответствуют две линии и два уравнения регрессии. Одно из них характеризует регрессию V по U, т.е. V =f(U), а другое – регрессию U по V, т.е. U =f (V) (рис.1).

рис.1 рис.2 рис.3

Геометрический смысл коэффициентов регрессии заключается в следующем (рис.1):

1. коэффициенты а_v/u и а_u/v численно равны отрезкам, отсекаемым соответствующей линией регрессии на осях координат: а_v/u – на оси V, а_u/v – на оси U. При а_v/u =0 и а_u/v =0 линии регрессии проходят через начало координат;

2. коэффициенты b_v/u и b_u/v численно равны тангенсам углов наклона линии регрессии к соответствующей оси координат: b_v/u = tg  (к оси U), b_u/v = tg  (к оси V), если значения U и V центрированы и нормированы по стандарту, т.е. соответствуют величинам 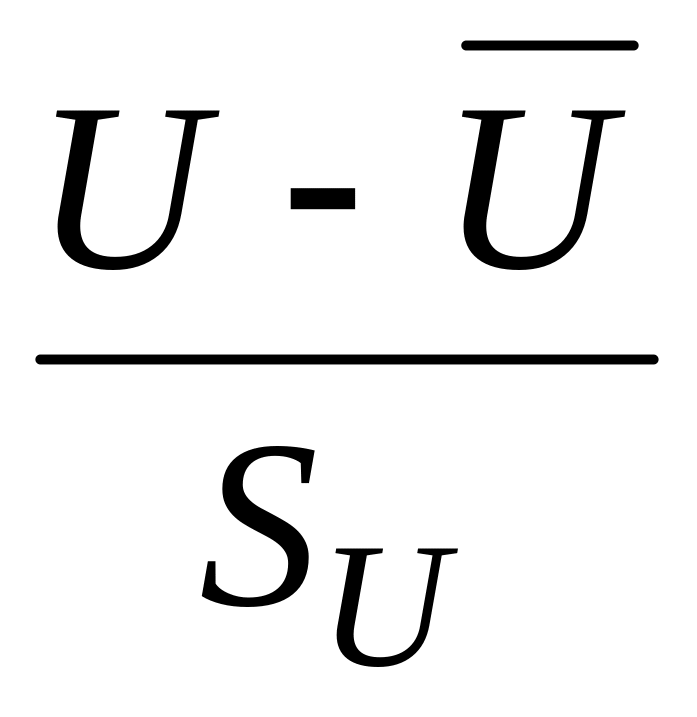и ;

3. линии регрессии пересекаются в точке с координатами и , а косинус угла между ними характеризует тесноту корреляционной связи (cos  = r). При =0 обе линии сливаются в одну, и зависимость между U и V становится функциональной (cos 0 = 1 = r), а при =90 зависимость между U и V отсутствует (cos 90 = 0).

Коэффициенты регрессии вычисляют двумя способами: 1) методом наименьших квадратов; 2) с помощью выборочных оценок средних, дисперсии и коэффициента корреляции.

Суть метода наименьших квадратов заключается в таком подборе теоретической линии регрессии, чтобы отклонения эмпирических данных от теоретической линии регрессии были бы минимальными, причем при регрессии V по U минимизируются отклонения по ординате (V), а при регрессии U по V – по абсциссе (U) (рис.2). При этом минимизируется вся сумма отклонений, т.е. учитываются как положительные, так и отрицательные отклонения, но чтобы они не погасили взаимно друг друга, минимизируются не сами отклонения, а их квадраты.

Поэтому условие минимизации при выборе линейного уравнения вида V = а+ b U опреде-ляется выражением . После дифференцирования этого выражения и приравнивания нулю частных производных по коэффициентам а и b получают систему следу-ющих двух уравнений: .

Решение этой системы уравнений дает следующие формулы для вычисления коэффици-ентов а и b при регрессии V по U :

, .

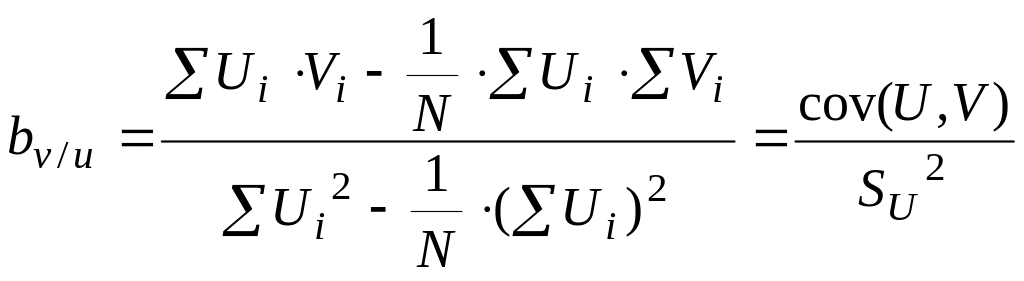При регрессии U по V аналогичные формулы коэффициентов а и b имеют вид: , .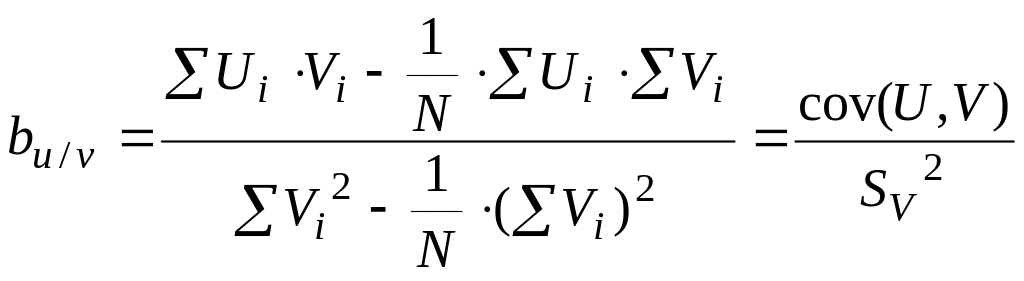

Во втором способе коэффициенты регрессии b рассчитываются через коэффициент кор-реляции и стандартные отклонения S_U и S_V по формулам: и ,

а коэффициенты регрессии а - по формулам: и .

Следует отметить, что уравнение линейной регрессии может быть рассчитано путем минимизации суммы квадратов отклонений от теоретической прямой не по осям координат, а по нормали к линии регрессии (рис. 3). Такое уравнение называется уравнением ортогональной среднеквадратической регрессии. Оно наилучшим образом описывает двумерное распределение. На корреляционном графике линия ортогональной регрессии проходит между линиями простой регрессии, но не обязательно посредине.

Коэффициенты уравнения ортогональной регрессии определяются следующим образом. Сначала вычисляется тангенс двойного угла 2 между линией ортогональной регрессии и положительным направлением оси абсцисс по формуле . После этого опреде-ляется угол 2, а затем сам угол . Величина угла 2 зависит от знаков r и tg 2. В зависимости от сочетания этих знаков распределение угла 2 по четвертям окружности (рис.4, 5, 6 и 7) и значения самих углов  (в радианах) окажутся следующими:

при r >0 tg 2>0 (1 четв.) = 0,5 arc tg 2 при r <0 tg 2>0 (3 четв.) = 0,5 (+arc tg 2)

tg 2<0 (2 четв.) = 0,5 (+arc tg 2) tg 2<0 (4 четв.) = 0,5 (2+arc tg 2).

После определения угла  находят его тангенс, значение которого и составляет величину коэффициента b ортогональной регрессии, т.е. b= tg . Коэффициент регрессии а определяют по формуле .

рис.4 рис.5 рис.6 рис.7

Следует отметить, что на вид уравнений регрессии очень сильно влияют аномальные (вы-дающиеся) значения двумерной совокупности. Для их исключения из выборки используется эл-липс рассеяния двумерного нормального распределения (Мягков и др., 1989). Для уровня зна-чимости =0,05 эллипс строится по уравнению, получаемому из выражения:

= 6,0516.

Аномальными считаются значения, выходящие за пределы контурного эллипса. После их исключения следует рассчитать новое уравнение регрессии без учета выдающихся значений.

Корни уравнения эллипса рассеяния для 5%-го уровня значимости можно рассчитать по формуле (Мягков и др., 1989): .

При нелинейной корреляции, т.е. когда    r , необходимо подобрать вид уравнения связи, ориентируясь, во-первых, на форму эмпирической линии регрессии, построенной на корреляционном графике, во-вторых, исходя из содержательного анализа изучаемого явления. Обычно для этого используются алгебраические полиномы второй, реже третьей и более высоких степеней, гиперболические, логарифмические, показательные и экспоненциальные функции. Расчеты коэффициентов регрессии таких нелинейных уравнений проводят тем же методом наименьших квадратов, но предварительно нелинейные уравнения приводят к линейному виду, т.е. линеаризуют, что значительно упрощает все вычисления.

Например, гиперболическая функция Y=a+b/X (при Х0) приводится к линейному виду Y=а+bХ₁ путем замены исходной переменной X новой переменной X₁=1/X, т.е. в расчетах коэффициентов регрессии участвуют не исходные значения X_i, а их преобразования 1/X_i.

Логарифмические функции Y=а+blgХ или Y=а+blnХ приводятся к линейному виду Y=а+ bХ₁ путем замены исходной переменной X новой переменной Х₁=lgХ или Х₁=lnХ.

Квадратические функции Y=а+bХ² или Y=а+bХ приводятся к линейному виду Y=а+ bХ₁ путем замены исходной переменной X новой переменной Х₁=Х² или Х₁=Х.

Степенные функции Y=aX^b приводятся к линейному виду Y₁=а₁+bХ₁ после логарифми-рования исходной функции Y=aX^b и приведения ее к виду lnY=lna+blnX с последующей заменой обеих исходных переменных X и Y новыми переменными Х₁=lnХ и Y₁=lnY.

Показательные функции Y=ab^X, Y=а10^bX или Y=10^a+bX приводятся к своим линейным эквивалентам соответственно lg Y=lg a+X lg b, lgY=lga+bX и lgY=a+bX с последующей заменой: в первом случае обеих исходных переменных X и Y новыми переменными Х₁= =lgХ и Y₁=lgY, а во втором и третьем - заменой переменной Y новой переменной Y₁=lgY.

Экспоненциальные функции Y=aе^bX или Y=е^a+bX приводятся к своим линейным эквивалентам lnY=lna+bX или lnY=a+bX с последующей заменой исходной переменной Y новой переменной Y₁=lnY.

Во всех перечисленных случаях все расчеты по определению коэффициентов регрессии производятся не с исходными значениями Х_i , Y_i или Х_i и Y_i , а с их преобразованиями.

Доверительные интервалы для коэффициентов а и b уравнения простой линейной регрессии вида V = а+ b U рассчитываются по формулам (Клименко, Пахомов, 1991, с. 120):

• для коэффициента а: 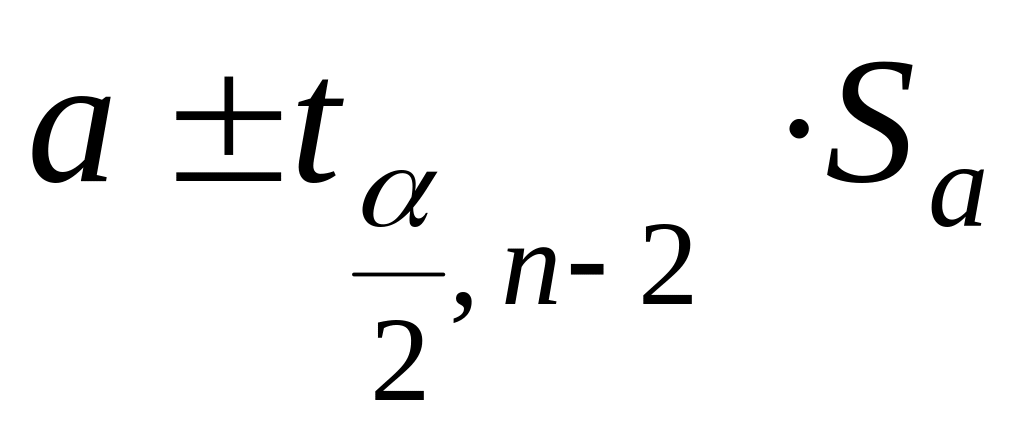, где , ,

, ;

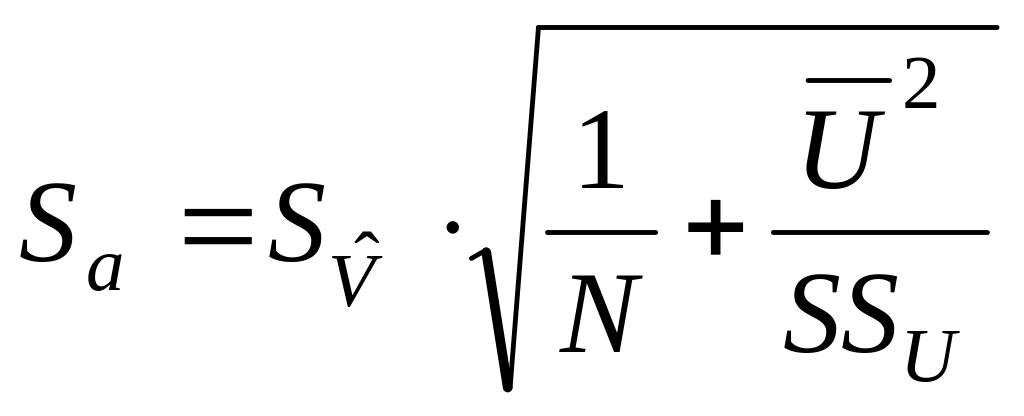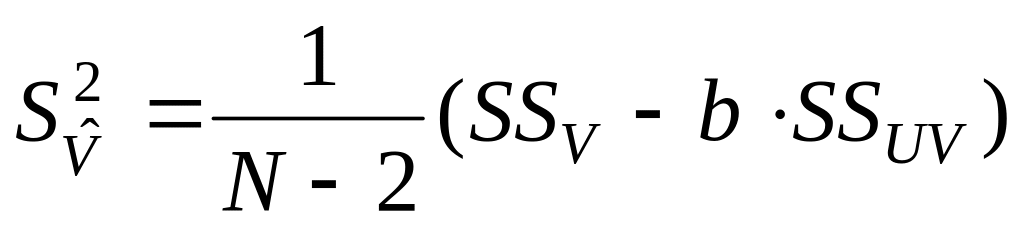• для коэффициента b: 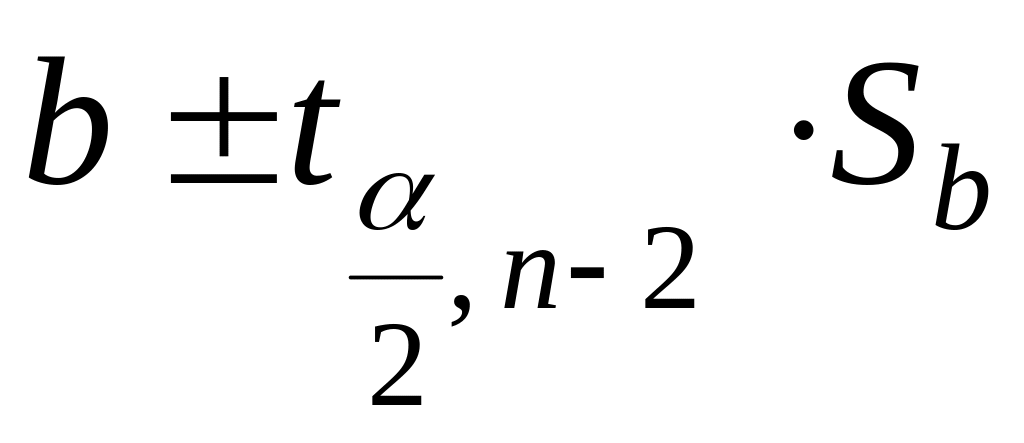, где .

Доверительный интервал расчетного значения в зависимости от величины U рассчитываются по формулам (Клименко, Пахомов, 1991, с. 120):

, .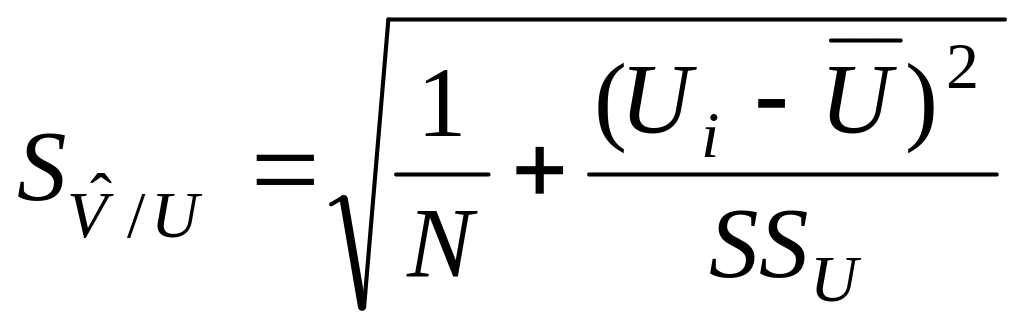