4. Оценки параметров распределения. Доверительные интервалы. Проверка гипотез.

Математическая статистика – наука, служащая для обработки экспериментальных данных.

Х – генеральный признак(фактор). - набор значений величины Х полученный из какого-то эксперимента или выборка из генеральной совокупности. Какой должна быть выборка?

Требуется, чтобы она представляла всю генеральную совокупность. Единственный способ - считать, что элементы выборки появляются случайно или независимо в соответствии с истинным по неизвестным нам законам распределения F(x) генеральной совокупности Х.

Выборка обладающая таким свойством называется репрезентативной (представительной).

Пусть - k различных элементов из выборки.

- эти элементы называются варианты. Варианты – разные элементы выборки расположенные по возрастанию.

-число повторений соответствующих вариантов (частоты вариантов).

, , ,

,

Оценка параметров распределения.

Пусть Х имеет закон распределения F(x), который нам известен, но в него входит неизвестный набор параметров или параметр θ(тэта). , θ – параметр.

- выборка из генеральной совокупности Х

θ* - оценка

, - конкретные значения параметра.

- статистика - некоторая функция от выборки, с помощью которой что-то строится.

θ* - случ. величина.

- чем меньше разность, тем лучше оценка, разность случайная

Оценка определяется вероятностью, с которой , ε – заданное число. чем выше вероятность, тем оценка в принципе лучше.

Требования к оценкам.

1. Несмещенность. θ* - несмещенная оценка, если Mθ*=θ. θ* - смещенная, при оценивании содержится некоторая системная ошибка.

2. Эффективность.

θ* - эффективная, если она имеет наименьшую возможную дисперсию, это значит, что чаще всего оценка будет мало отличаться от среднего значения.

3. Состоятельность.

θ* - состоятельная если, (оценка некоторой с.в. построенная по выборке).

Если оценка соответствует этим требованиям, в среднем она лучше.

Оценка мат.ожидания.

Х – ген. случайная величина, - выборка из ген. совокупности. Естественная оценка - среднее арифметическое выборочных данных, среднее выборочное.

- варианты, - частоты.

В соответствии с общим стат. признаком, то что мы называем мы должны рассматривать как значение случайной величины , которая вычисляется , где - независимые с.в. распределенные как генеральная величина Х.

Сравним качество этой оценки.

1.Несмещенность.

- несмещенная оценка.

- несмещенная оценка

не хуже, чем оценка .

2.Эффективность.

асимптотическая эффективность.

Оценка асимптотически эффективна.

3. Состоятельность(стремление к оценке параметров п.в.)

в силу ЗБЧ.

Оценка несмещенная, асимптотически эффективная, состоятельная, значит ей можно пользоваться.

Оценка дисперсии.

D[X] генеральная дисперсия.

(в - выборочная) это естественная оценка для дисперсии(левая часть равенства). Если использовать частоты вариант, то эта же оценка приобретает вид правой части равенства.

1.Несмещенность.

для простоты m – истинное мат ожидание, m=MX.

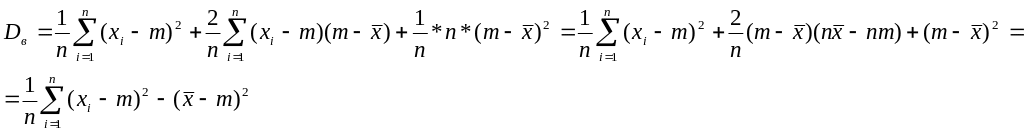
эта оценка слегка смещенная, она будет слегка занижать величину дисперсии.

лучше пользоваться пи больших объемах выборки(больше 30), при малых используется вторая оценка.

- оценка,

- исправленная выборочная дисперсия, при малых объемах выбора лучше пользоваться ей.

На практике - лучше вычислять не по исходной формуле, а по

Метод моментов.

Х – ген. выборка имеет закон распределения F(x, θ)

- выборка.

рассмотрим какой-нибудь теоретический момент(вероятностный) Х, и приравняем его к статическому анализу.

Если нам надо узнать несколько параметров, то надо соответственно записать столько моментов, сколько параметров и решить полученную систему.

Примеры:

1. , - неизвестные, оценить их по выборке.

2. - требуется оценить числа a и b имея выборки .

Метод максимального правдоподобия.

X, F(x, θ) известен с точностью до параметра.

- выборка.

1. Х – дискретная.

Составляем функцию , где .

Функция L – функция правдоподобия и она задает вероятность, что в эксперименте будет получена выборка .

Чтобы получить оценку для θ, надо функцию L максимизировать. , θ – аргумент L.

Элементы выборки превращаются в параметры функции L. На практике удобнее максимизировать не саму функцию L, а логарифм этой функции .

- решение этого уравнения дает нам оценку θ. Если параметров несколько ( ), то рассматриваются такие же, только будет система из частных производных ,

2. Х – непрерывная с.в.

В этом случае функция L идейно составляется также, но вместо вероятностей плотность.

, - плотность Х, при условии, что параметр есть θ.

Часто оценки по методу моментов и методу правдоподобия совпадают.

Пример:

Оценить параметр λ для с.в. имеющей распределение Пуассона.

,

- результат эксперимента(последовательности испытаний)

- число успехов в бесконечной последовательности испытаний.

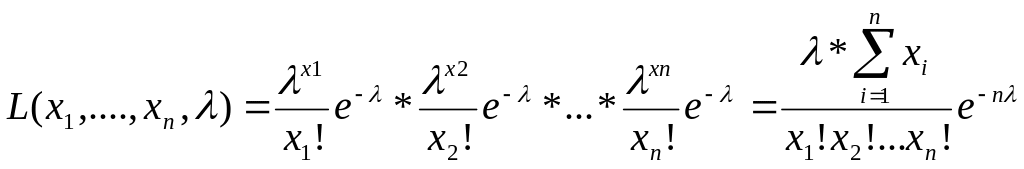- функция правдоподобия.

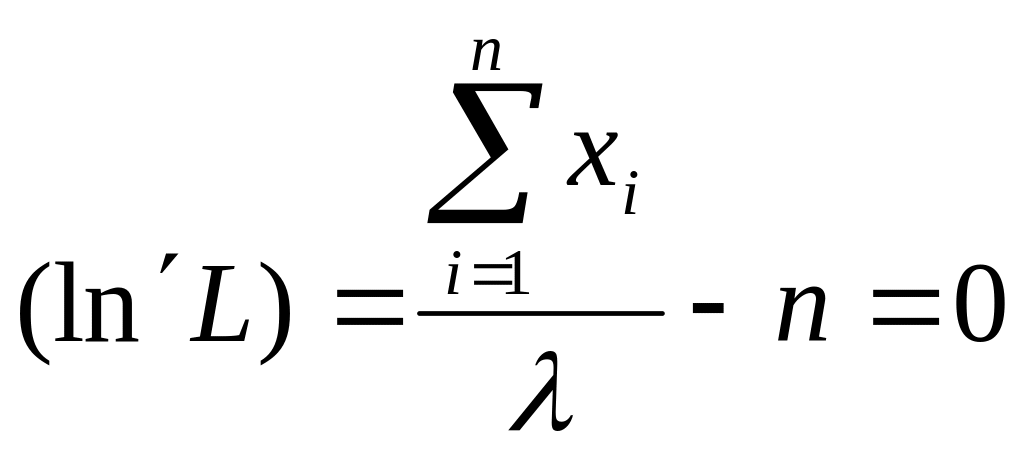
Оценка 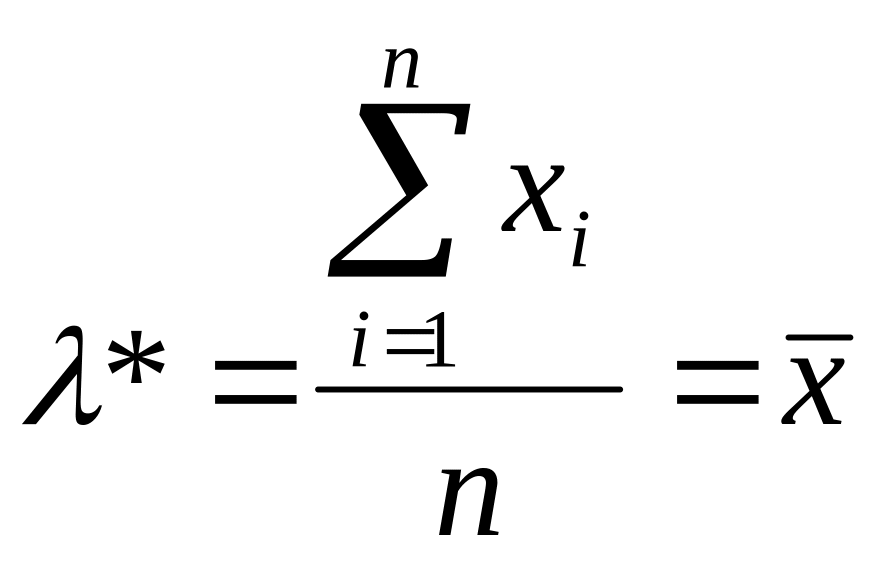- среднее выборочное. Вывод: оценкой λ является среднее выборочное.

Интервальные оценки.

Оценки параметра θ полученные в предыдущих темах называются точечными.

Пусть θ* - некоторая точечная оценка параметра θ.

θ- θ* - эта разность есть величина случайная, т.к. - функция от выборки, а выборка случайная.

, α – называется доверительной вероятностью или надежностью, σ характеризует точность оценки.

- доверительный интервал- интервал, на котором истинное θ находится с вероятностью α. Случайным здесь является сам интервал, отсюда интервал с заданной вероятностью должен накрыть истинное но неизвестное значение θ.

Задание 1.

Построение доверительного интервала для оценки мат. ожидания нормальной величины с известной дисперсией.

, σ – неизвестно.

,

Пусть ,

,

- доверительный интервал, классический доверительный интервал.

при точность оценки возрастает (длина интервала уменьшается).

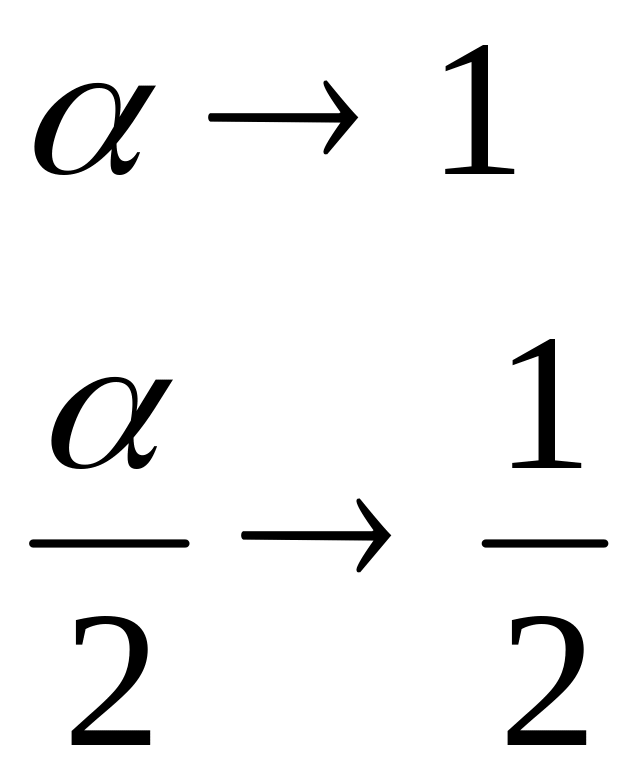
, функция Лапласа, отсюда

Задача 2.

Посторенние доверительного интервала для оценки мат.ожидания нормальной величины с неизвестной дисперсией.

, σ – неизвестно, m- неизвестно(его надо оценить используя выборку из генеральной совокупности)

Лемма.

Пусть одинаковые независимые случайные величины =>

а) и независимы друг от друга

б)

Доказательство:

т.к. дисперсия не меняется при сдвиге, можно без ограничения общностей считать, что мат.ожидание m=0, отсюда ,

Пусть , , - некоторый коэф., положим .

При этом

Эти числа можно подобрать так, что С будет ортогональна, т.е. каждая строка-вектор единичной длины , и также

Также скалярное произведение двух любых различных строк=0.

Матрица С осуществляет преобразование системы . По сути ортогональное преобразование есть поворот осей относительно начала координат. При этом длины векторов не меняются и сохраняются углы между векторами, из этого следует , - нормальная величина с характеристиками:

, ,

, .

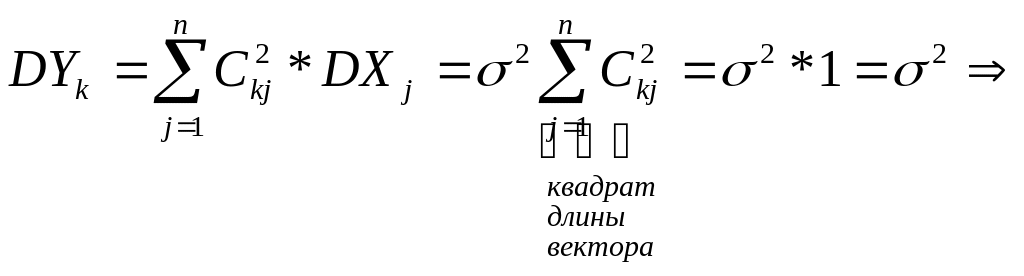
Выясним, являются ли у-ки независимыми, для этого надо сосчитать ковариацию между двумя у-ми.

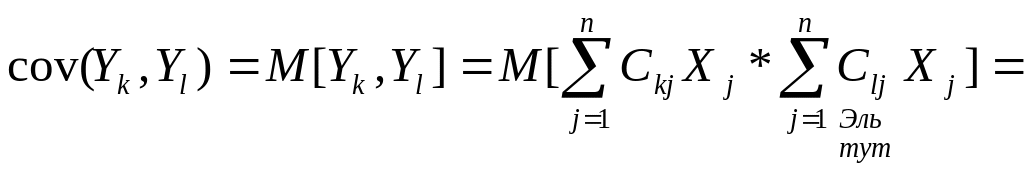, , когда раскроем скобки, все слагаемы с разными номерами будут иметь мат.ожидание=0 .

Вывод: Ковариация двух любых различных у-ков есть 0, некор-ть и независимость совпадают, все у-ки попарно-независимы между собой.

, ,

, .

1. В итоге V – есть сумма квадратов стандартных нормальных величин, число слагаемых (n-1), со степенью свободы (n-1), то есть . Число степеней свободы – число независимых переменных. Пункт а) следует из того, что выражается через , а выражается через комбинацию всех у-ков кроме . , , 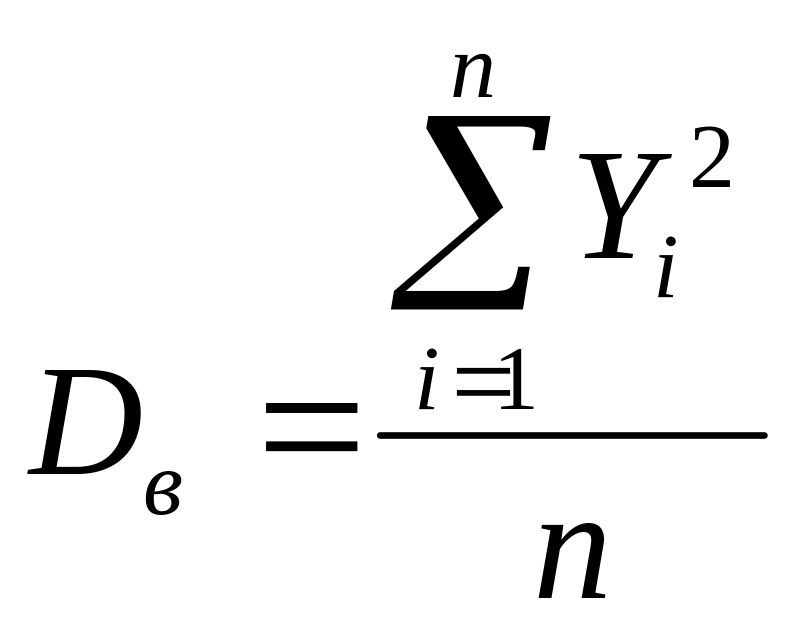следовательно, эти величины независимы.

, .

, распределение Стьюдента,

, т.к. .Отсюда, если взяли величину z она стандартная величина нормальная.

.

z и : заменяем на S и распределение получилось почти нормальным.

Зададимся α точностью: , число находится по таблице коэффициентов Стьюдента при заданном α и n (или n-1). Допустим, что нашли .

, - доверительный интервал.

Доверительный интервал для оценки дисперсии нормальной величины.

оценить σ по выборке из генеральной совокупности.

из леммы.

q находится по таблице в которой надо ввести n, α (Гмурмана).

доверительный интервал с q из таблицы Гмурмана.

,

и находятся по таблице распределения с (n-1) степенями свободы и заданной надежностью α.

Таблица критических точек распределения .

Опр. Критическая точка данного распределения – такая точка, для которой задана вероятность оказаться правее ее.

критическая точка

критическая точка

Чаще используется таблица , лучше пользоваться доверительным интервалом для (дисперсия).

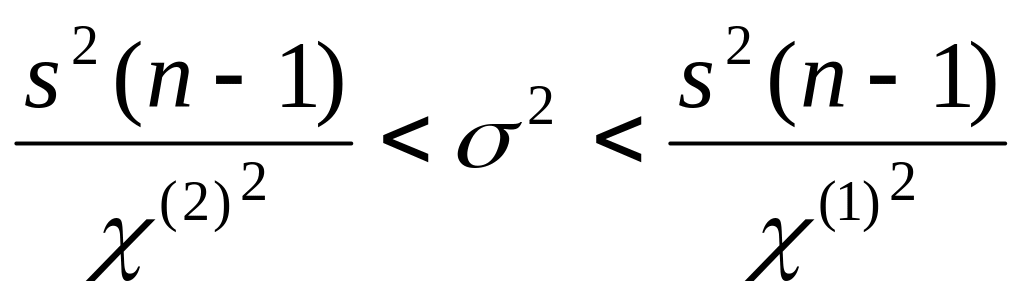, , находятся точно так же как , но по таблице крит. распределения .

Проверка статических гипотез.

Статической гипотезой будем называть утверждение либо о параметре распределения, либо о самом законе распределения.

Простые и сложные гипотезы:

Простая гипотеза содержит предложение о единственном значении параметра, а сложная о многих значениях параметра.

- простая гипотеза, (m – мат.ожидание)

- сложная гипотеза (т.к. « > 0» это бесконечное количество).

Если - сложная гипотеза, обычно рассматриваются две гипотезы:

- основная гипотеза

- конкурирующая гипотеза.

всегда противоречит , но необязательно, что является логическим отрицанием.

.

- основная гипотеза

- конкурирующая гипотеза.

Ошибки при принятии гипотез.

решение принять или .

	Нет ошибки	Ошибка I рода
	Ошибка II рода	Нет ошибки

то, что есть на самом деле (т.е. эти гипотезы верны).

Ошибка I рода – отвергнуть правильную гипотезу (пропуск цели).

Ошибка II рода – принять неправильную гипотезу (ложная тревога).

Ошибки могут иметь разные последствия.

Пример.

	Болен	Здоров
Болен		Принять больного за здорового
Здоров	Принять здорового за больного

Проверка гипотез осуществляется с помощью критерия.

Критерий

- вектор = х (n-мерный случайный вектор)

- совместная плотность = ( n-мерная плотность),

Определим критическое множество:

если , если .

Вероятность ошибки I рода – это вероятность отвергнуть гипотезу . Вероятность ошибки I рода

Зафиксируем вероятность ошибки γ ошибки I рода. Число γ – уровень значимости. При фиксированном γ выбрать такое критическое множество s чтоб β была минимальной.

Определим величину , если , то и мы ничего не получим, если , то , W – мощность критерия s.

Максимальный по мощности критерий называется max или оптимальным критерием.

Лемма(Неймона-Пирсона).

Для двух простых гипотез оптимальный критерий существует.

Если хотя бы одна из гипотез не является простой, то max по мощности критерия обычно не существует. В этом случае пользуются равномерно наибольшим по мощности критерием.

, s – критическое множество.

На практике рассматривается отображение s на некоторое множество K: , К – критическое множество на прямой.

.

Основные виды критических множеств K:

1. Двусторонняя критическая область.

2. Правосторонняя критическая область.

3. Левосторонняя критическая область.

Опр. Точки отделяющие критические области называются критическими точками.

Окончательное правило: Если отношение большей дисперсии к меньшей больше чем критическая точка, то отвергаем. Если это отношение меньше F критической, то оснований отвергнуть у нас нет.