6.* Параметрычны спосаб задання агульных крывых.

7*. Гладкія(рэгулярныя) элементарныя урывыя. Эквівалентныя параметрызацыі.

8.Яўнае заданне плоскай крывой ў дэкартавых каардынатах.

Гэта заданне крывой раўнаннем выгляду:

Вырашана адносна адной з дэкартавых каардынат.

У гэтым выпадку, кажуць так сама, што крывая зададзена як графік ф-цыі:

Сцв. Плоская крывая дапускае яўнае заданне ў дэкартавых каардынатах калі і толькі калі, яна адназначна праектуецца на адну з дэкартавых восей.

Заўвага: Крывая, якая зададзена яўна, дапускаюць наступныя простыя параметрызацыі:

1)

2)

9*. Яўнае заданне прасторавай крывой ў дэкартавых каардынатах

10.Няяўнае заданне плоскай крывой у дэкартавых каардынатах.

Гэта заданне крывой раўнаннем выгляду:

Гэта значыць не вырашаным адносна якой-небудзь каардынаты.

Раўнанне (1) наз. Неяўным раўнаннем крывой ў дэкартавых каардынатах.

Т-ма: Няхай ёсць мн-ва ўсіх пунктаў пл-ці, каардынаты якіх адрозніваюцца ў нуль вектарам ў кожным пункце , тады кожны пункт мае наваколле перасячэнне з ёсць элементарная гладкая крывая.

Пункты крывой зададзеннай раўнаннем

Наз. Асаблівым пунктам гэтага задання, калі ў ім

Крывыя могуць дапускаць заданні, як з асаблівымі пунктамі, так і без іх, ў гэтым выпадку будзем выкарыстоўваць іх заданні без асаблівых пунктаў.

11*.Няяўнае заданне прасторавай крывой ў дэкартавых каардынатах.

Гэтае яе заданне сіс-май раўнанняў выгляду

Як лінія перасячэння двух паверхняў.

Ур-нне (2) наз. Не яўным раўнаннямі адпаведна прасторавай крывой.

Т-ма: Няхай мн-ва пунктаў у пр-ры каардынаты якіх задавальняюць раўнанняў (2). Калі уздоўж вектары

Існуюць непарыўны і вектарны здабытак

Тады кожны пункт мн-ва мае наваколле перасячэння якога з ёсць гладкая э.к.

Пункт крывой зададзенай раўнаннямі (2) ў якім

Наз. Асаблівым пунктам, дадзенага неяўнага задання.

Прасторавая крывая часам можа дапускаць няяўнае заданне, як з асаблівымі пунктамі, так і не з асаблівымі пунктамі. Тады будзем выкарыстоўваць другое заданне( без асаблівых пунктаў)

12*. Заданне крывых у недэкартавых каардынатах.

На пл-ці(ў пр-ры) увесці недэкартавыя каардынаты, напрыклад палярныя на пл-ці, сферычныя ці цыліндрычныя –у пр-ры, тадыможна разглядзець непараметрычныя спосабы задання крывых адносна гэтых новых каардынат, аналагічна папарэдняму.

ПР: Оρφ , тады адносна ёй крывыямогуць дапускаць яўнае заданне

Няяўнае заданне:

Параметрычнае заданне:

У прыватнасці –палярная раўнанне крывой, яно часта выкарыстоўваецца. Крывую зададзенную ім зручна параметрызаваць так:

13. Датычная прамая крывой.

Азн.: датычнай прамой крывой у яе пункце Р наз. лімітавае становішча яе сякучай PQ, пры умове, што пункт Q неабмежавана набліжаецца да пункта Р, рухаючыся па крывой . Будзем абазначаць: Т

Тэарэма:

1. (Існаванне) Усякая гладкая крывая γ у кожным сваім пункце Р мае датычную прамую Т і прычым толькі адну.

2. (адзінасць) Калі 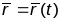, 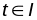- адвольная дапушчальная параметрызацыя гладкай крывой γ, тады век-тарнае параметрычнае раўнанне яе датычнай пра-мой Т у яе п. Р можна запісаць у выглядзе: 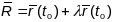,λ∈ℝ.

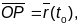
Доказ: 1. Калі 0 – пачатак сістэмы каардынат, тады 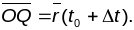Вектар 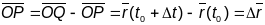кіроўны вектар сечнай прамой PQ. Вектар - кіроўны вектар сечнай PQ. Калі на 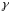, 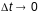і паколькі 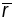- галдкая параметрызацыя крывой існуе і адрозніваецца ад 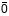. . Відавочна прамая Т, якая будзе праходзіць праз Р у напрамку гэтага вектара і будзе лімітавым становішчам пераменнай сякучай PQ. 2. Няхай 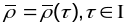- іншая далучаная пара-метрызацыя крывой 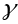эквшвалентна яе параметрызацыі 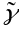. Г.зн. 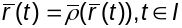. 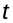Дыфферэнцыруя па будзем мець 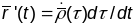. 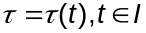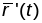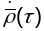Паколькі якабіан зменнай параметра адрозніваецца ад , атрымалі, што і у адным і тым жа пункце Р каленіарныя. Такім чаным, у гэтым пункце яны вызначаюць адну і тую ж прамую Т, для якой з’яўляюцца кіроўнымі вектарамі.

3. (канструк-тыўнасць) Вывад раўнання: Нахай - радыўс-вектар бя-гучага пункта М датычнай прамой Т. , .

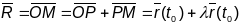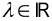Вынік: Калі - адвольная дапушчальная параметрызацыя гладкай крывой , тады вектар 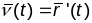есць кіроўны вектар датычнай прамой крывой у яе пункце с вектарам хуткасці параметра 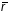у адвольным пункце.

14.Нармаль плоскай крывой.

Нармаллю крывой 𝛄 у яе пункце Р наз. Прамая N, якая праходзіць праз гэты пункт P, перпендыкулярна датычнай прамой T

Абазначаецца праз N.

Сцв1: Усякая гладкая крывая γ ў кожным сваім пункце Р мае адзіную нармаль N. Кіроўны вектар ёсць нармальны вектар датычнай прамой у пункце P.

Сцверджанне2: Калі гладкая крывая γ зададзена неяўна 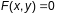і пры гэтым 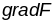непарыўны і адрозніваецца ад 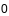у яе пункце, тады вектар 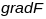з’яўляецца кіроўным вектарам нармалі N ці, што таксама нармальным вектарам датычнай прамой да крывой у пункце .

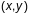Доказ: Выбярэм некаторую параметрызацыю крывой 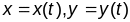. Тады ўздоўж будзем мець тоеснасць 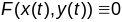. Дыфферэнцыруя па гэтая роўнасць , , , .
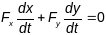
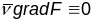
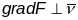