Построение эпюр изгибающих моментов и перерезывающих сил.

Ввиду симметрии нагрузки и конструкции рамы эпюры изгибающих моментов и перерезывающих сил строятся для одной ее половины.

Каждый стержень рамы рассматривается как однопролетная свободно опертая балка, находящаяся под воздействием заданной нагрузки и найденных опорных моментов. При построении эпюр используются таблицы элементов изгиба балок [1] для отдельных видов нагрузок. Эпюры изгибающих моментов и перерезывающих сил приведены на рис. 2.3.

Подробное описание построения эпюр рассмотрено в предыдущей задаче ( см. п. 1.4 ).

В результате решения задачи получены следующие максимальные значения моментов и перерезывающих сил :

стержень 1-5 124,6 кНм ; 121,9 кНм;

стержень 1-2 35,2 кНм ; 34,6 кНм;

стержень 2-3 9,3 кНм ; 5,1 кНм;

стержень 2-6 50,2 кНм ; 43.9 кНм;

стержень 3-4 9,2 кНм ; 14,4 кНм.

­2.3. Задача 3. Расчет перекрытия с большим числом балок главного направления и одной перекрестной связью.

2.3.1. Условия задачи 3.

Для перекрытия с одной перекрестной связью и большим числом балок главного направления определить элементы изгиба перекрестной связи посредине пролета и в опорных сечениях. Рассчитать среднюю и крайние балки главного направления и построить для них эпюры изгибающих моментов и перерезывающих сил.

2.3.2. Краткие сведения из теории.

Теория изгиба плоских судовых перекрытий основана на следующих предположениях:

в каждом узле перекрытия балки главного направления и перекрестные связи имеют одну связь, обеспечивающую равенство прогибов балок в узле. Вследствие этого в узловых точках возникают сосредоточенные реакции взаимодействия R между балками, нормальные к плоскости перекрытия (рис.3.1)

вся внешняя распределенная по площади перекрытия нагрузка Q₁(x) воспринимается балками главного направления, а каждая перекрестная связь загружена реакциями ее взаимодействия с балками главного направления и действующими непосредственно на нее внешними распределенными и сосредоточенными усилиями Q₂ и P.

В дальнейшем рассматриваются только регулярные перекрытия, у которых все балки главного направления одинаковы, имеют одинаковые опоры и расположены на равном расстоянии друг от друга. Расчет регулярного перекрытия с одной перекрестной связью и большим числом балок главного направления (более пяти) при принятых выше допущениях сводится к расчету перекрестной связи как балки, лежащей на сплошном упругом основании (см. рис3.2). Упругим основанием для перекрестной связи служат балки главного направления.

В этом случае изгиб перекрестной связи описывается дифференциальным уравнением

E I w^IV + k w = q(x). (3.1)

Здесь и на рис. 3.1 и 3.2 введены следующие обозначения:

L – длина перекрытия ;

l – ширина перекрытия ;

a – расстояние между балками главного направления ;

I – момент инерции площади поперечного сечения перекрестной связи ;

I – момент инерции площади поперечного сечения балок главного на- правления;

Q(x) – суммарная распределенная нагрузка интенсивности q(x) на пере- крестную связь, состоящая из нагрузок Q₂ и Q₃ ;

R_j – реакция взаимодействия перекрестной связи с j- вой балкой главного направления ;

w – упругая линия перекрестной связи ;

k – коэффициент жесткости упругого основания, на котором лежит пере- крестная связь.

Интенсивность нагрузки q(x) представляет собой сумму интенсивностей q₂(x) и q₃(x) нагрузок Q₂ и Q₃. При этом под Q₃ следует понимать часть действующей на балки главного направления нагрузки Q₁, которая передается на перекрестную связь в составе реакции R. Ее интенсивность определяется зависимостью

где β – коэффициент влияния нагрузки Q₁(x) на прогиб j- вой балки главного направления в узловой точке ;

γ – коэффициент влияния реакции R_j на прогиб узловой точки балки глав- ного направления.

В выражении (3.2) при координате x опущен индекс j , так как предполагается, что при большом числе балок главного направления сосредоточенные реакции можно заменить распределенной на расстоянии а нагрузкой.

Коэффициент жесткости упругого основания находится из выражения

При расчете перекрытий на изгиб считаются заданными геометрические и жесткостные характеристики балок перекрытия, условия их опирания на опорном контуре и действующие на перекрытие нагрузки. Поэтому можно считать известными коэффициенты EI и κ и правую часть в дифференциальном уравнении (3.1).

Решение дифференциального уравнения (3.1) позволяет найти упругую линию w(x) перекрестной связи. Для определения изгибающего момента М(х) и перерезывающей силы N(x) , действующих в поперечных сечениях перекрестной связи, используются известные соотношения :

М(х) = ЕIw^II, (3.4)

N(x) = EIw^III. (3.5)

Реакция взаимодействия перекрестной связи с j-вой балкой главного направления равна

R_j = a [EIw^IV – q₂] = a [q₃(x_j) – kw(x_j)]. (3.6)

При известных реакциях R_j и внешней нагрузке Q₁(x) элементы изгиба балок главного направления могут быть определены методом наложения с помощью таблиц изгиба балок [ 1 ]. Обычно ограничиваются определением реакций со стороны перекрестной связи на крайнюю и среднюю балки главного направления. При нахождении первой из них предполагается, что балка главного направления жестко оперта на перекрестную связь.

Остановимся на решении дифференциального уравнения (3.1). Оно имеет вид

w(x) = w_о.у(x) +w_ч.р(x), (3.7)

где w_о.у – общий интеграл однородного уравнения;

w_ч.р – частное решение.

Общий интеграл однородного уравнения w_о.у. может быть представлен в нескольких формах. Подробно эти формы решения и их выбор в конкретных задачах изложены в учебниках [2], [3]. Среди них наибольшее употребление в задачах изгиба балок на упругом основании имеют функции Пузыревского. В этом случае решение однородного уравнения представляется в виде

w_о.у. = D₀V₀(αx) + D₁V₁(αx) + D₂V₂(αx) + D₃V₃(αx), (3.8)

где V_i(αx) – функции Пузыревского,

D_i при i=0,1,2,3 – произвольные постоянные интегрирования, которые определяются из граничных условий на концах перекрестной связи;

Аналитические выражения для функций Пузыревского содержатся в учебниках [2], [3]. Для облегчения применения в расчетах имеются таблицы этих функций в справочнике [1]. Следует заметить, что в справочнике [1] представлены функции Пузыревского для умеренных значений аргумента αx₀ (αx₀ < 3,5, x₀ – абсцисса сечения, для которого производят вычисление функции). При увеличении аргумента αx₀ значения функций V_i(αx₀) быстро растут, что приводит к вычислительным трудностям – появлению малой разности близких величин в решении системы уравнений, определяющей произвольные постоянные D_i. Поэтому при больших значениях аргумента αx₀ расчет при определении D_i необходимо выполнять с большим числом значащих цифр. Отметим, что в справочнике [4] функции Пузыревского представлены в диапазоне [0:10] для значений аргумента αx₀ От малой разности близких величин можно избавиться, если вместо функций Пузыревского в решение (3.8) ввести определенным образом функции Клишевича [2, с. 107].

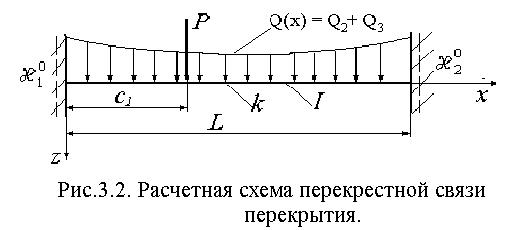
Функции Пузыревского есть линейно независимые частные решения однородного уравнения, удовлетворяющие следующим условиям при x = 0 :

(3.9)

При дифференцировании по x функции Пузыревского переходят одна в другую

по следующему закону: 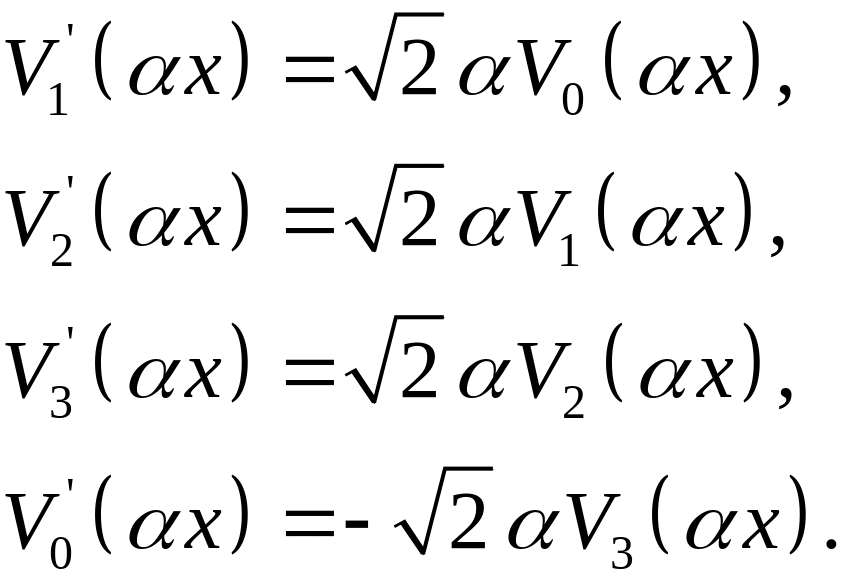(3.10)

Частное решение w_чр(x) уравнения (3.1) зависит от вида правой части. Оно имеет наиболее простое решение для случая, когда в пролете балки приложена непрерывная распределенная нагрузка, представленная полиномом не выше третьей степени

q(x) = a + bx +cx² +dx³. (3.11)

В этом случае

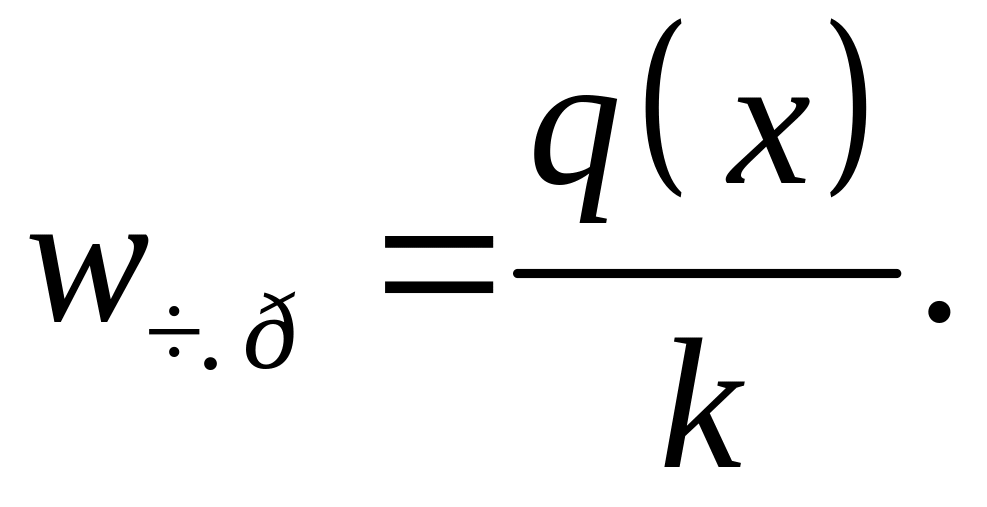(3.12)

При воздействии на балку нагрузки, имеющей разные законы изменения на разных участках по длине балки может быть найдено методом начальных параметров [ 2, с. 108]. Так, для достаточно общего случая нагрузки, изображенного на рис.3.3 частное решение может быть записано в виде 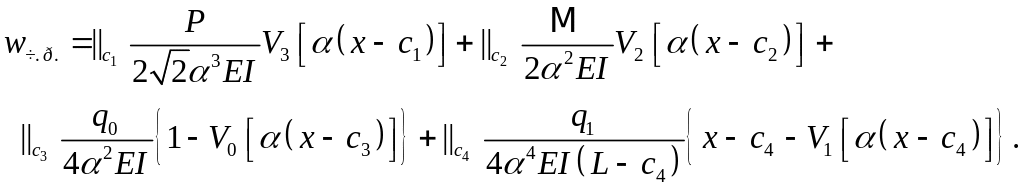(3.13)

В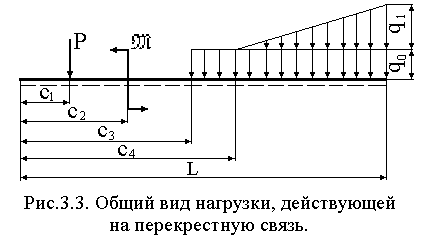 ыражение (3.13) получено в предположении, что приложенная к балке распределенная нагрузка непрерывна вплоть до конца пролета балки. Поэтому в случае действия на балку распределенной нагрузки, не доходящей до конца пролета, следует ее продлить до правого конца с одновременным приложением к балке на продлеваемом участке нагрузки противо- положного знака.

Заметим, что при определении произвольных постоянных интегрирова- ния D_i граничным усло- виям должно удовлетво- рять полное решение (3.7).

В частном случае, когда балка загружена симметричной нагрузкой и

симметрично заделана на опорах, упругая линия балки может быть записано в виде

(3.14)

где

w₀(x), w₁(x) – упругие линии балки соответственно в случаях ее свободного опирания и жесткой заделки на концах;

• - коэффициент опорной пары.