30. Производная по направлению
Предположим теперь, что функция f (М) дифференцируема в точке М. Приращение функции f(М) в точке М вдоль прямой l можно записать в виде
.
где
– бесконечно малые функции при Δ l → 0.
Разделив обе части равенства на Δl и
учитывая, что
,
получим
.
Переходя к пределу в этом равенстве при Δl → 0 , получаем формулу для производной по направлению
.
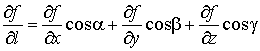Из этой формулы
следует, что производная по направлению
является линейной комбинацией частных
производных, причем направляющие
косинусы являются коэффициентами,
показывающими вклад в производную по
направлению от соответствующей частной
производной. В частности,
при
,
при
.
Из этого следует, что частные производные по х, у, z являются частными случаями производной по направлению осей координат.
31. Градиент.
Градиентом функции z = f (М), в точке М (х, у, z ) называется вектор, координаты которого равны ответствующим частным производным
,
взятыми в точке М( х, у, z )
.
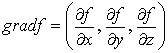Используя понятие
градиента функции, и учитывая, что вектор
имеет ординаты
,
представим формулу в виде скалярного
произведения векторов
и вектора
.
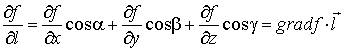С другой стороны, по определению скалярного произведения имеем
.
Учитывая, что
,
получаем
.
Из последнего равенства следует, что производная функции по направлению имеет наибольшую величину при cosφ = 1 (φ = 0), т.е. когда направление вектора совпадает с
направлением grad
f. При этом
.
Таким образом, градиент функции z = f (М)
в точке М ( х, у, z ) характеризует направление
и величину максимальной скорости
изменения этой функции в данной точке. Соотношение для дифференциала функции
f (М)
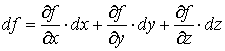
можно представить в векторном виде, если ввести вектор перемещения
и воспользоваться скалярным произведением в координатной форме
.
Полный дифференциал скалярной функции равен скалярному произведению градиента функции на дифференциал вектора перемещения.
32. Понятие двойного интеграла, его свойства вытекающие из определения.
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в замкнутой
области D плоскости Оху задана непрерывная
функция z=ƒ(х;у). Разобьем область D на n
«элементарных областей»
площади которых обозначим через ΔSi, а
диаметры (наи большее расстояние между
точками области) - через di(см. рис. 3).
В каждой области Di выберем произвольную точку Mi(xi;yi), умножим значение ƒ(хi;уi) функции в этой точке на ΔSi и составим сумму всех таких произведений:
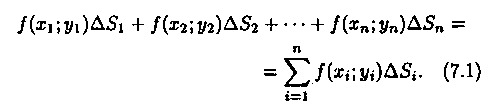
Эта сумма называется интегральной суммой функции ƒ(х;у) в области D.
Рассмотрим предел интегральной суммы (7.1), когда n стремится к бесконечности таким образом, что maxdi -> 0. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции ƒ(х;у) по области D и обозначается
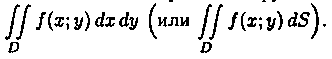
Таким образом, двойной интеграл определяется равенством
В этом случае функция ƒ(х;у) называется интегрируемой в области D; D - область интегрирования; х и у - переменные интегрирования; dxdy (или dS) - элемент площади.
1
2
3
,где
k-константа
4.Если
в области R, то
;
5.Если
в области R , то
;
6.Если
на R и области R и S являются непересекающимися
то
.
Здесь
означает объединение этих двух областей.