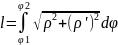- •Теорема о связи первообразной и функции. Понятие неопределенного интеграла
- •Свойства неопределенного интеграла. Интегрирование по частям. Круговой интеграл
- •1. Линейность:
- •2. Инвариантность формы интеграла:
- •3. Интегрирование по частям:
- •Интегрирование рациональных функций (1 теорема Остроградского).
- •Интегрирование иррациональных функций (подстановка Эйлера)
- •Интегрирование тригонометрических функций (универсальная тригонометрическая подстановка).
- •Вычисление площади криволинейной трапеции.
- •7) Замена переменной в определенном интеграле.
- •7)Понятие определенного интеграла
- •10. Вычисление длины дуги графика функции
- •11) Вычисление объема тела вращения
- •12) Несобственные интегралы, теорема сравнения
- •13. Теорема Коши, формулировка для дифференциального уравнения первого порядка.
- •14)Однородные дифференциальные уравнения первого порядка.
- •Дифференциальные уравнения с разделяющимися переменными
- •Дифференциальные уравнения в полных дифференциалах
- •Неполные дифференциальные уравнения, допускающие понижения порядка
- •Ду, не зависящие явно от у
- •2)Ду, не зависящие явно от х
- •Линейные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение
- •Линейная независимость решений ду. Определитель Вронского
- •Структура общего решения неоднородного линейного ду
- •21)Метод вариации произвольных постоянных
- •22) Линейные ду с квазимногочленом в правой части
- •23) Преобразования Лапласа. Изображения тождественной, единичной и показательной функции
- •24) Теорема линейности, подобия. Теорема затухания-смещения
- •25) Теорема о дифференцировании оригинала
- •26)Теорема о Дифференцировании изображения. Изображение свертки
7) Замена переменной в определенном интеграле.
Пусть функция f(x) непрерывна на [a;b], а функция x=ϕ(t) непрерывно дифференцируема на отрезке [α;β], причем ϕ(α)=a, ϕ(β)=b и значения функции ϕ(t) не выходят за пределы отрезка [a;b], когда t ϵ [α;β]. Тогда

x |
a |
b |
t |
|
β |
Интегрирование по частям.
Если функции
 и
и
 непрерывно дифференцируемы на отрезке
[a;b], то
непрерывно дифференцируемы на отрезке
[a;b], то
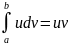 |ba
-
|ba
-
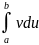
7)Понятие определенного интеграла
Понятие определенного интеграла
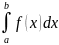 функции
функции
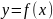 ,
заданной на отрезке [a;b],
является одним из центральных в
математическом анализе. Конструкция
определенного интеграла включает в
себя следующие три момента. 1.Разиваем
отрезок [a;b]
точками x1 на
части:
,
заданной на отрезке [a;b],
является одним из центральных в
математическом анализе. Конструкция
определенного интеграла включает в
себя следующие три момента. 1.Разиваем
отрезок [a;b]
точками x1 на
части:
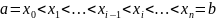
Обозначим через
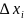 отрезки
отрезки
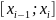 ,
а также их длины
,
а также их длины
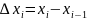 .
Выберем точки
.
Выберем точки
 Получим отмеченное разбиение. 2. По
отмеченному разбиению составляем
интегральную сумму функции f(x);
Получим отмеченное разбиение. 2. По
отмеченному разбиению составляем
интегральную сумму функции f(x);

Геометрически интегральная сумма
представляет из себя площадь ступенчатой
фигуры, состоящей из прямоугольников,
в основании которых лежат отрезки
,
а высоты равны
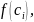 если
если
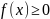 «Мелкость» разбиения измеряется
диаметром разбиения d=maxi
,
т.е. длиной наибольшего отрезка разбиения.
«Мелкость» разбиения измеряется
диаметром разбиения d=maxi
,
т.е. длиной наибольшего отрезка разбиения.
Определенным интегралом от функции
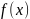 по отрезку [a;b],
или в пределах от a до b,
называется предел интегральных сумм
при стремлении диаметра разбиения к
нулю:
по отрезку [a;b],
или в пределах от a до b,
называется предел интегральных сумм
при стремлении диаметра разбиения к
нулю:
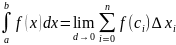
Если указанный предел существует независимо от выбора отмеченных разбиений, то функция f(x) называется интегрируемой(по Риману). Можно доказать, что если функция ограничена на отрезке [a;b] и непрерывна на нем, кроме, быть может, конечного числа точек разрыва, то она интегрируема.
Геометрический смысл определенного
интеграла заключается в том, что
равен площади криволинейной трапеции,
лежащей над отрезком [a;b]
и ограниченной сверху (если
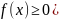 графиком функции
.
графиком функции
.
8. Замена переменной в определенном интеграле. Этот метод позволяет упростить вычисления, т. е. привести подынтегральное выражение к соответствующей табличной форме. Применение замены переменной в определенном интеграле базируется на следующей теореме.
Теорема. Если функция f(x) непрерывная на отрезке [a; b], а функция x=φ(t) непрерывно дифференцируема на отрезке [t1; t2], причем φ([t1; t2])=[a; b] и φ(t1)=a, φ(t2)=b, то справедлива формула:
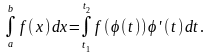
при вычислении определенного интеграла методом подстановки (замены переменной) делать обратную замену не надо, нужно только пересчитать пределы интегрирования.
9. Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ=ρ(θ) и двумя полярными радиусами θ=α, θ=β (α < β), выражается интегралом:

10. Вычисление длины дуги графика функции
Элемент дуги кривой dl находится по теореме Пифагора:
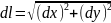
дифференциал функции y=f(x)
или х=х(t) находится по
формуле
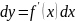 ,
соответственно
,
соответственно
 .
.
1) если кривая задана графиком
функции y=f(x),
a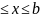 ,
то её длина
,
то её длина
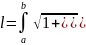
2) если кривая задана параметрическими
уравнениями x=x(t),
y=y(t),
 ,то
,то
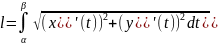
3) в случае пространственной кривой
x=x(t),
y=y(t),
z=z(t),
α

4) если кривая задана в полярных
координатах уравнением ρ=ρ(φ),
φ1 φ
φ2,
то
φ
φ2,
то