2. Векторное произведение векторов.

Векторным произведением двух векторов и является вектор , обладающий следующими свойствами:

1) его длина равна произведению длин двух векторов на синус меньшего угла между ними,

2) он перпендикулярен плоскости, в которой лежат оба исходных вектора, а значит, перпендикулярен каждому из исходных векторов,

3) его направление выбрано так, что векторы , и составляют правую тройку. То есть если направить средний палец правой руки по вектору , а большой – по вектору , то указательный примет направление вектора .

Обозначение векторного произведения: или . Из определения имеем: , , . Кроме того, справедливы свойства и .

Нетрудно заметить, что .

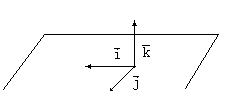
Запомнить, какой орт получается как векторное произведение двух других ортов, легко, если пользоваться следующей схемой.

Если при движении от первого в векторном произведении вектора ко второму мы движемся против часовой стрелки, результатом векторного произведения будет третий вектор со знаком +, если по часовой стрелке, то третий вектор со знаком –.

Представляя векторы и с координатами, соответственно, и в виде разложения по базису , и пользуясь свойствами векторного произведения, получим:

.

Запомнить векторное произведение в координатной форму проще всего с применением определителя:

.

Выражение в правой части последнего равенства называется определителем третьего порядка. Подробнее об определителях будет сказано в следующей лекции, а сейчас следует запомнить, что данный определитель можно вычислить следующим образом. Добавим в имеющуюся структуру, состоящую из трех строк и трех столбцов снизу дополнительно две первые строки. В полученной структуре, состоящей из трех столбцов и пяти строк, проведем всевозможные диагонали от первого столбца к третьему, содержащие по три элемента из разных столбцов. Значение определителя получается как сумма произведений по три элемента, стоящих на одной диагонали, причем если диагональ идет сверху вниз слева направо, берется знак +, если сверху вниз справа налево, берется знак –.

Из определения векторного произведения следует, что векторное произведение двух ненулевых векторов и равно нулю тогда и только тогда, когда векторы и параллельны.

2. Смешанное произведение векторов.

Смешанным произведением трех векторов , и называется скалярное произведение . Из определений скалярного и векторного произведений следует, что если все три вектора , и , участвующие в смешанном произведении, лежат в одной плоскости, то .

Если координаты векторов , и равны, соответственно, , и , то смешанное произведение вычисляется с помощью определителя третьего порядка: .

2. Векторы произвольной размерности.

По аналогии с двумерными и трехмерными векторными пространствами рассматривают векторные пространства размерности , где – произвольное натуральное число. Такой вектор уже не изобразишь графически, и представляет он собой упорядоченный набор из координат: . При записи многомерного вектора верхнюю стрелку над буквой не изображают.

-мерные векторы можно умножать на число: , складывать: и скалярно умножать друг на друга: .