Лабораторная работа №2 Числовые характеристики и законы распределения случайных величин

Биномиальное распределение

Пусть имеются n испытаний Бернулли с вероятностью успеха p и вероятностью неуспеха q, p+q=1. Дискретная случайная величина X – число успехов имеет распределение

При этом

Математическое ожидание и дисперсия случайной величины:

Геометрическое распределение

Дискретная случайная величина X имеет геометрическое распределение, если она принимает значения k=1,2,3,… (счетное множество значений) с вероятностями При этом

Случайная величина X, имеющая геометрическое распределение, представляет собой число испытаний Бернулли до первого успеха.

Математическое ожидание и дисперсия случайной величины:

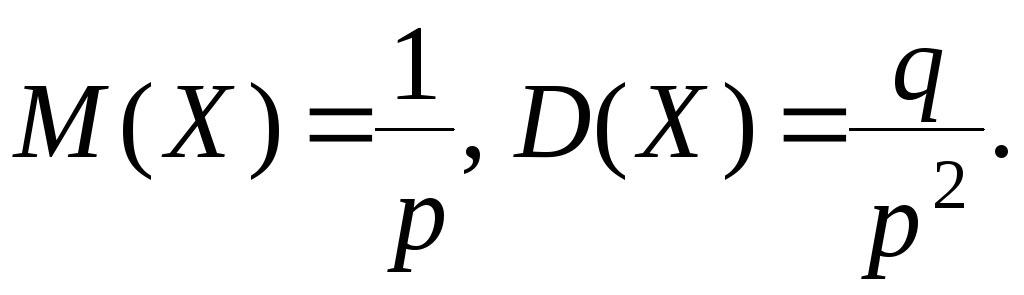
Гипергеометрическое распределение

Дискретная случайная величина X имеет гипергеометрическое распределение, если она принимает значения m с вероятностями

Вероятность p_m является вероятностью выбора m объектов, обладающих заданным свойством, из множества n объектов, случайно извлеченных (без возврата) из совокупности N объектов, среди которых M объектов обладают заданным свойством.

Математическое ожидание и дисперсия случайной величины:

Распределение по закону Пуассона

Дискретная случайная величина X имеет распределение по закону Пуассона, если она принимает значения k=0,1,2,… с вероятностями При этом

Математическое ожидание и дисперсия случайной величины:

Равномерное распределение

Непрерывная случайная величина X распределена равномерно на отрезке [a;b], если ее плотность вероятности p(x) постоянна на этом отрезке и равна нулю

вне его,

Функция распределения случайной величины, распределенной по равномерному закону, имеет вид

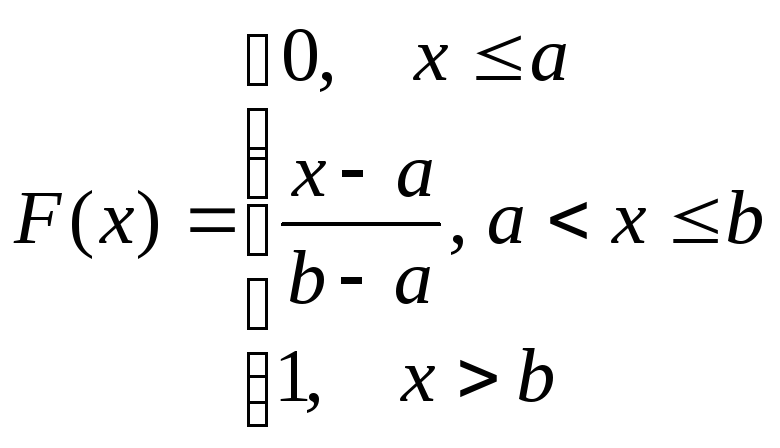
Математическое ожидание и дисперсия случайной величины:

Показательное (экспоненциальное) распределение

Непрерывная случайная величина X имеет показательное распределение с параметром λ>0, если ее плотность вероятности p(x) имеет вид,

Функция распределения случайной величины, распределенной по показательному закону, имеет вид

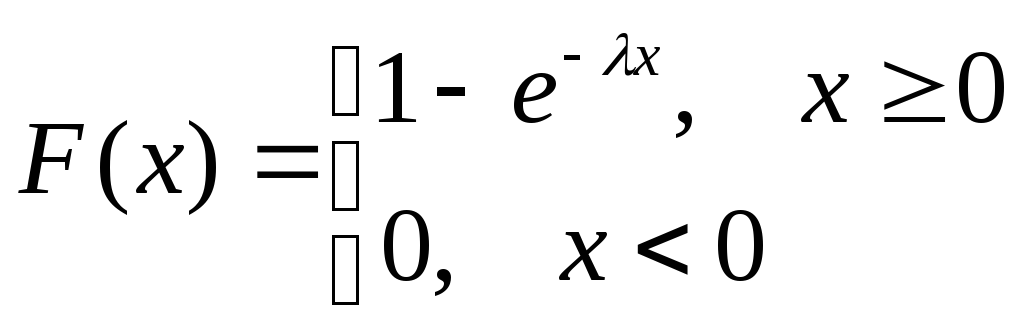
Математическое ожидание и дисперсия случайной величины:

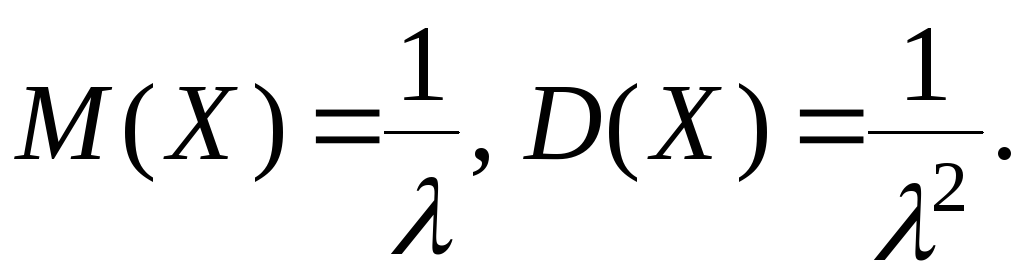
Нормальное распределение

Непрерывная случайная величина X имеет нормальный закон распределения с параметрами a и σ>0, если ее плотность вероятности p(x) имеет вид,

Обозначим через N(a;σ) множество случайных величин, распределенных по нормальному закону с параметрами a и σ. Функция распределения нормальной случайной величины XN(a;σ) имеет вид

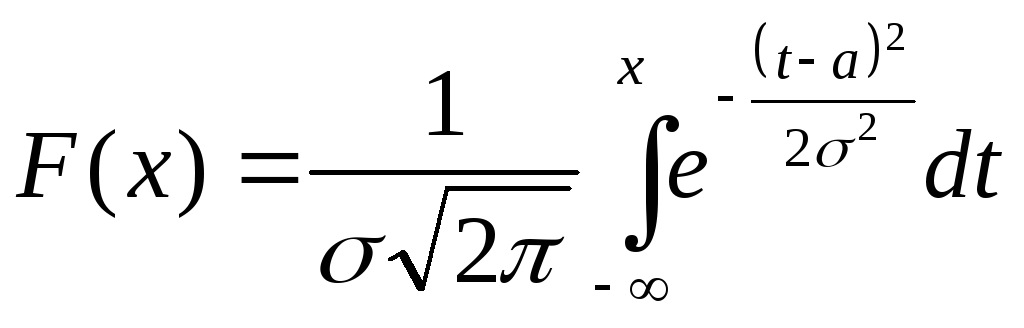
Математическое ожидание и дисперсия случайной величины:

При a=0, σ=1 распределение называется стандартным нормальным. Множество таких распределений обозначается N(0;1). Для стандартного распределения плотность вероятности равна . Введенная ранее функция Лапласа Ф(x) задает вероятность попадания случайной нормальной величины X в интервал (0,x).

Пусть X N(a;σ), тогда вероятность того, что X принимает значения из интервала (x1,x2), можно вычислить, используя функцию Ф(x), по формуле

Числовые характеристики распределения случайной величины

Мода (Мо) – значение признака, наиболее часто встречающееся в исследуемой совокупности, т. е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту (или частость)

Модой Mo(X) случайной величины X называется ее наиболее вероятное значение, т. е. значение случайной величины, для которого вероятность (для дискретной величины) или плотность вероятности (для непрерывной величины) достигает максимума.

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным, если мода единственна, то распределение называется унимодальным.

• В дискретном ряду мода определяется визуально по максимальной частоте (или частости)

Пример 1: распределение женской обуви, проданной за месяц в магазине

Размер женской обуви (xi)	Число проданных пар, % к итогу (wi)
33 34 35 36 37 38 39 40	4 12 18 26 20 13 6 1
Итого:	100

Наибольшая частость равна 26 и соответствует варианте 36. Мо=36 Наибольшим спросом у женщин пользовался 36 размер.

• В интервальном ряду по наибольшей частоте определяется модальный интервал, а конкретное значение моды в интервале вычисляется по формуле

где x₀ – нижняя граница модального интервала, h – величина модального интервала, f_Мо, f_Мо-1, f_Мо+1 – частоты (или частости) модального, предмодального и послемодального интервалов.

Пример 2: данные о содержании влаги в поступившей партии товара в магазин:

Влажность, % (xi)	Число образцов (fi)
До 14 14 – 16 16 – 18 18 – 20 20 и более	20 30 25 15 10
Итого:	100

Наибольшая частота = 30 и соответствует интервалу 14 – 16 (модальный интервал)

Медиана (Ме) – значение признака (варианта), приходящееся на середину ранжированной (упорядоренной) совокупности, т. е. это вариант, который делит ряд распределения на две равные по объему части.

Медианой Me(X) непрерывной случайной величины X называется такое ее значение, для которого P(X<Me(X)) = P(X>Me(X))=1/2, т. е. вероятность того, что случайная величина X примет значение, меньшее медианы Me(X) или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая x=Me(X), проходящая через точку с абсциссой, равной Me(X), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке x=Me(X) функция распределения равна ½, т. е. F(Me(X))=1/2.

Алгоритм нахождения медианы:

• Рад ранжируют

• Вычисляют номер медианы (n – число единиц в совокупности)

• Вычисляют накопленные частоты (или частости)

• В дискретном ряду

Показатели признака: 3, 7, 2, 5, 2, 3, 9 (n=7, N=4)

Ранжируем: 2, 2, 3, 3, 5, 7, 9

Ме=3

Пример 1:

n=100, N=101/2=50,5. Накапливаем частоты до тех пор, пока кумулятивная частость не будет больше или равна номеру N.

Размер женской обуви (xi)	Число проданных пар, % к итогу (wi)	Накопленная частость (Si)
33 34 35 36 37 38 39 40	4 12 18 26 20 13 6 1	4 16 34 60 - - - -
Итого:	100

Ме=36

Одна половина обуви (50%) была продана 36 и менее размера, другая половина (50%) – 36 и более размера.

• В интервальном ряду значение медианы вычисляется по формуле

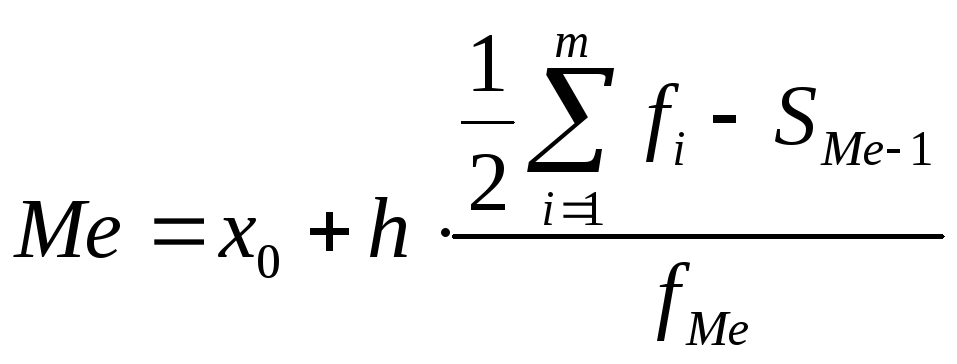
Где x₀ – нижняя граница медианного интервала, h – величина медианного интервала, f_Ме – частота медианного интервала, S_Ме-1 – накопленная частота предмедианного интервала.

Пример 2

n=100, N=101/2=50,5

Влажность, % (xi)	Число образцов (fi)	Накопленная частота (Si)
До 14 14 – 16 16 – 18 18 – 20 20 и более	20 30 25 15 10	20 50 75 - -
Итого:	100

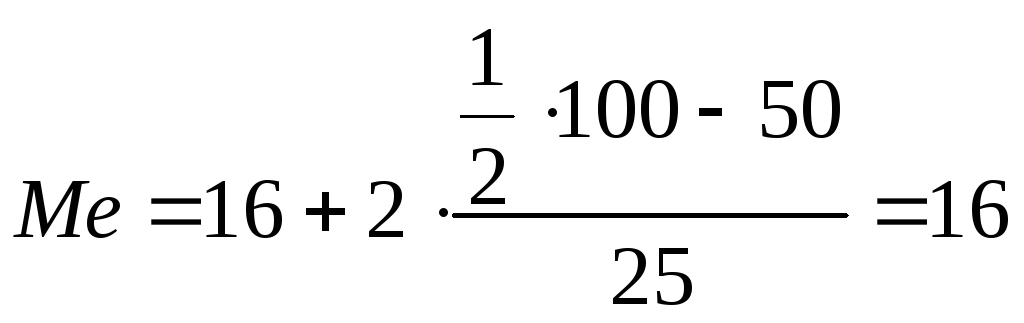
Одна половина (50%) партии товара имеет влажность 16% и менее, другая половина (50%) – 16% и более.