
- •Основы статистического анализа
- •1 Основные задачи статистического анализа
- •1.1 Выборочный метод
- •1.2 Основные задачи статистического анализа
- •Задача 1
- •Пример 1
- •2 Первичная статистическая обработка результатов наблюдений
- •2.1 Графическое представление данных
- •2.2 Числовые характеристики вариационного ряда
- •2.3 Интервальные оценки (доверительные интервалы)
- •2.4 Определение достаточного объема выборки
- •3 Сравнение двух выборок.
- •4. Статистическая оценка расхождения между выборочными частотами.
- •5. Сравнение долей
- •6. Исследование зависимостей
- •6.1. Постановка задачи
- •6.2. Линейная зависимость
- •6.4. Множественная линейная зависимость
2.3 Интервальные оценки (доверительные интервалы)
Пусть
![]() - произвольный неизвестный параметр
для признака
- произвольный неизвестный параметр
для признака
![]() и
и
![]() - его «хорошая» оценка. Будем писать это
символически
- его «хорошая» оценка. Будем писать это
символически
![]() ,
(1)
,
(1)
Понятно,
что предлагая в качестве оценки
![]() ,
мы будем иметь некоторую погрешность,
может быть даже достаточно большую,
поэтому естественно вместо (1) писать:
,
мы будем иметь некоторую погрешность,
может быть даже достаточно большую,
поэтому естественно вместо (1) писать:
![]() ,
(2)
,
(2)
где
![]() - величина погрешности, характеризующая
точность оценки
- величина погрешности, характеризующая
точность оценки
![]() .
Но оценка
.
Но оценка
![]() как функция от наблюдений
как функция от наблюдений
![]() является с.в. Поэтому еще более естественно
писать вместо (2):
является с.в. Поэтому еще более естественно
писать вместо (2):
![]() (Р
или 100Р %), (3)
(Р
или 100Р %), (3)
где
![]() -
вероятность, с которой гарантируется
данная точность
-
вероятность, с которой гарантируется
данная точность
![]() (т.е.
(т.е.
![]() ).
В частности, если
).
В частности, если
![]() ,
а
,
а
![]() ,
то с
,
то с
вероятностью
0.95 (в 95 % случаев) наша оценка
![]() гарантирует точность в пределах
гарантирует точность в пределах
![]() единиц.
единиц.
Таким
образом, мы пришли к определению
интервальной оценки или доверительного
интервала. Интервал
![]() называется интервальной
оценкой для
неизвестного параметра
называется интервальной
оценкой для
неизвестного параметра
![]() ,
соответствующим доверительной
вероятности
,
соответствующим доверительной
вероятности
![]() ,
если:
,
если:
![]() (4)
(4)
Читается
это так: вероятность того, что интервал
со случайными концами
![]() и
и
![]() накроет неизвестный параметр больше
или равна
накроет неизвестный параметр больше
или равна
![]() ,
величину
,
величину
![]() называют уровнем
доверия или
вероятностью
ошибки. Как
правило, при статистическом моделировании
в языковых исследованиях
называют уровнем
доверия или
вероятностью
ошибки. Как
правило, при статистическом моделировании
в языковых исследованиях
![]() .
.
Приведем теперь алгоритм построения
доверительного интервала для произвольного
параметра
![]() :
:
-
Найти «хорошую» оценку
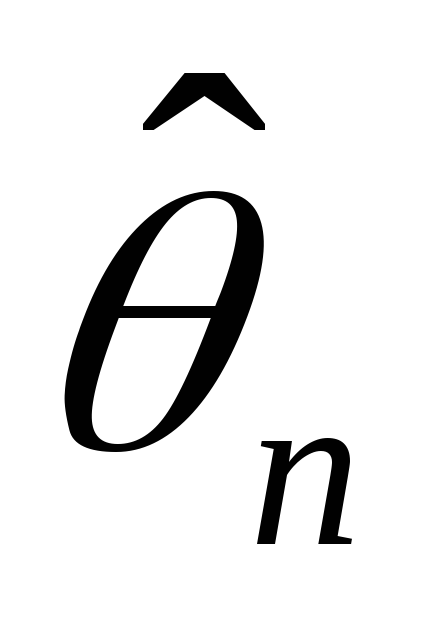 для
для
 ;
; -
Построить статистику
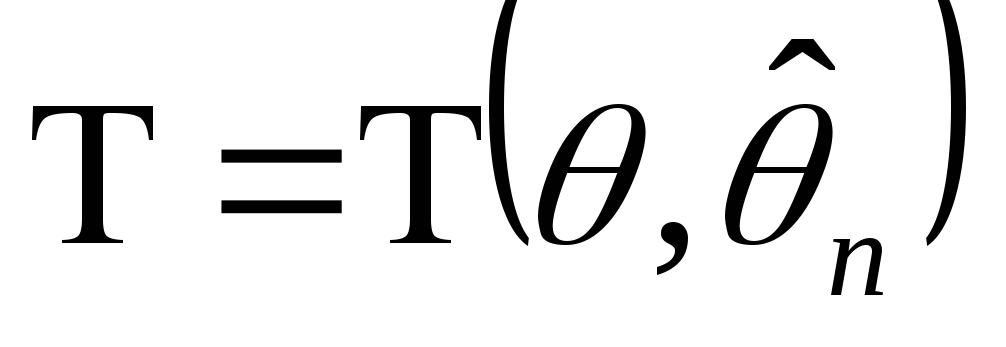 такую, чтобы она имела известный закон
распределения вероятностей (нормальный,
Стьюдента,
такую, чтобы она имела известный закон
распределения вероятностей (нормальный,
Стьюдента,
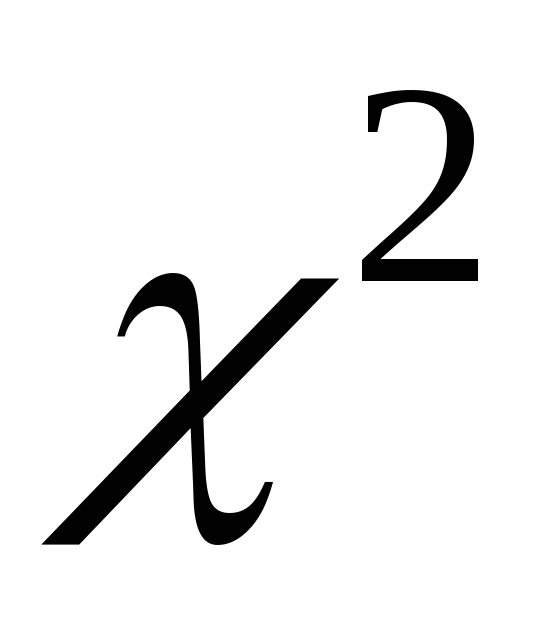 и т.д.). Тогда это распределение будет
затабулировано;
и т.д.). Тогда это распределение будет
затабулировано; -
Поскольку распределение статистики
 известно и затабулировано, то можно
определить вероятность
известно и затабулировано, то можно
определить вероятность
 для любого множества
для любого множества
 .
. -
Задаваясь теперь
 и исходя из природы статистики
и исходя из природы статистики
 (см. ниже пример), можно найти множество
(см. ниже пример), можно найти множество
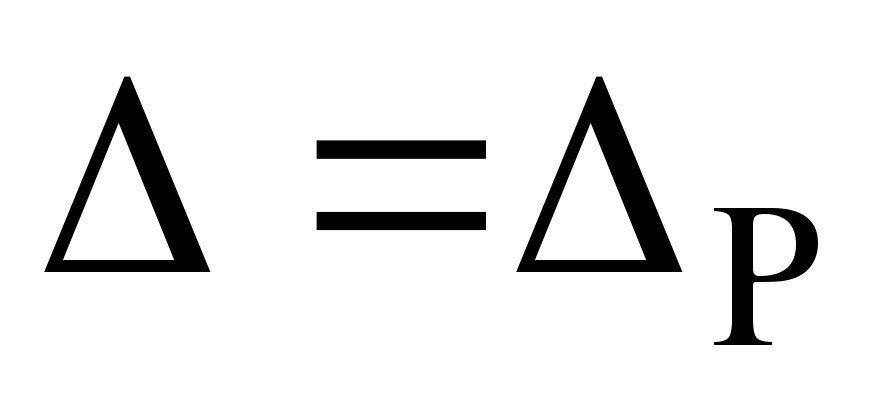 такое, что
такое, что
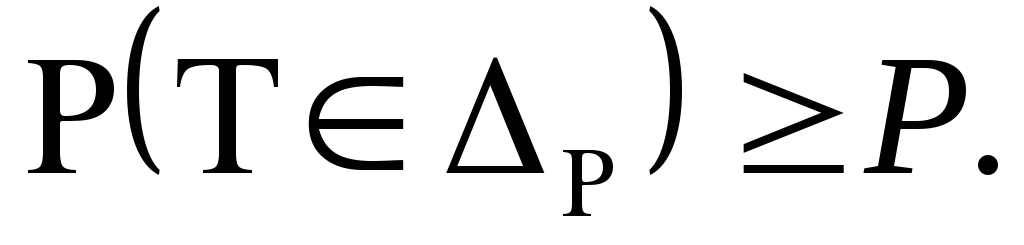
-
Пусть
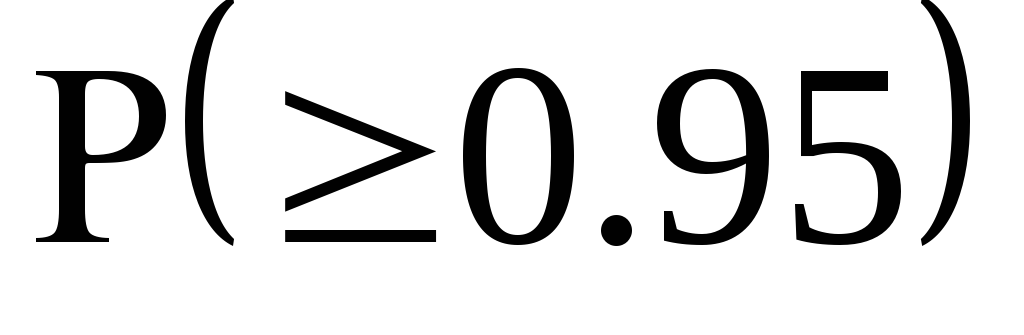 задана
задана

![]() ,
,
т.е.
тем самым построен доверительный
интервал
![]() ,
соответствующий доверительной вероятности
,
соответствующий доверительной вероятности
![]() .
.
Пример
5. Пусть наблюдается с.в.
![]() :
:
![]() ,
причем с.в. нормальна с параметрами
,
причем с.в. нормальна с параметрами
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
т.е. плотность
,
т.е. плотность
![]()

Предположим,
что неизвестным параметром распределения
является
![]() ,
т.е. мы хотим найти интервальную оценку
для
,
т.е. мы хотим найти интервальную оценку
для
![]() .Возможны
случаи:
.Возможны
случаи:
![]() а)
а)
![]() -
известна;
-
известна;
б)
![]() -
неизвестна;
-
неизвестна;
а)
![]() и
и
![]() .
.
-
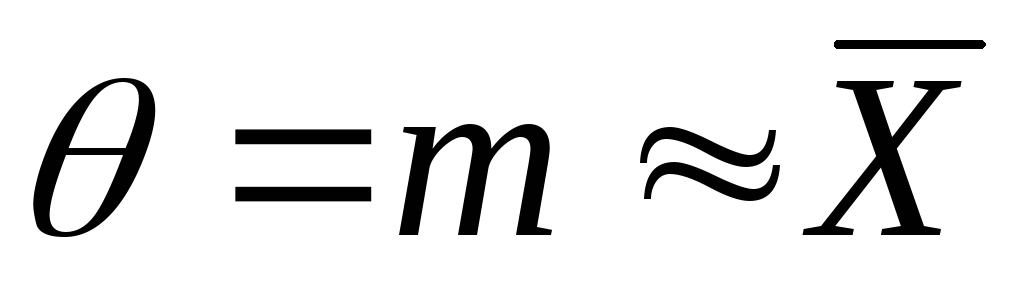 -
«хорошая» оценка;
-
«хорошая» оценка; -
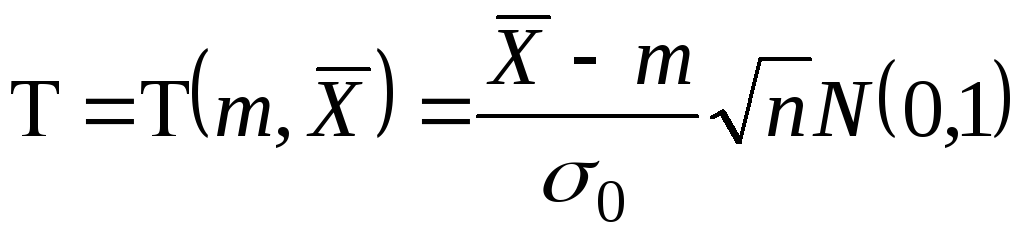 ;
; -
 -
определяется по таблице нормального
распределения для любого
-
определяется по таблице нормального
распределения для любого
 .
. -
Поскольку
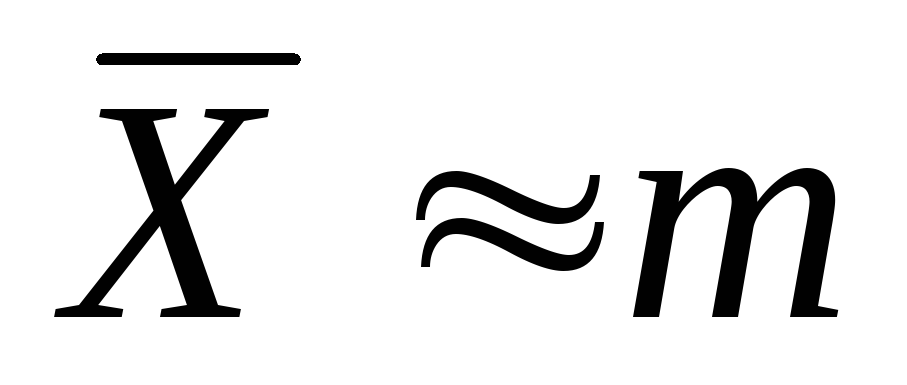 ,
то чем больше по модулю значение
,
то чем больше по модулю значение
 ,
тем больше погрешность, естественно,
поэтому взять:
,
тем больше погрешность, естественно,
поэтому взять:
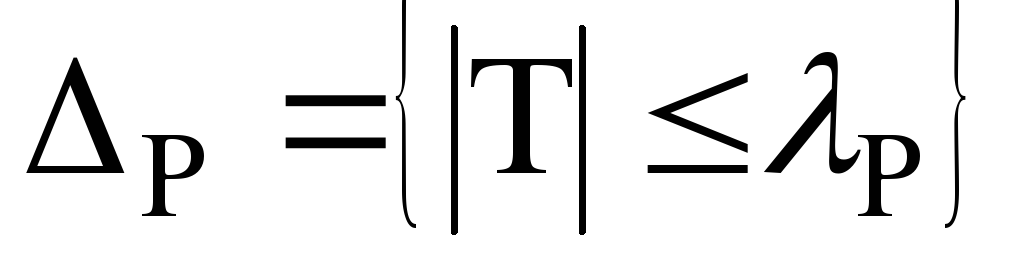 ,
где
,
где
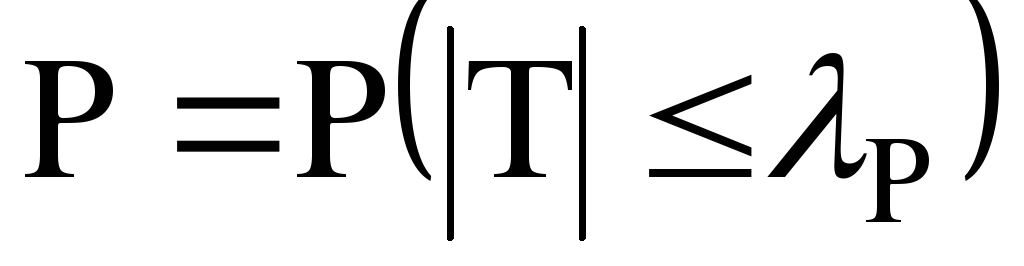 .
. -
Разрешая теперь относительно
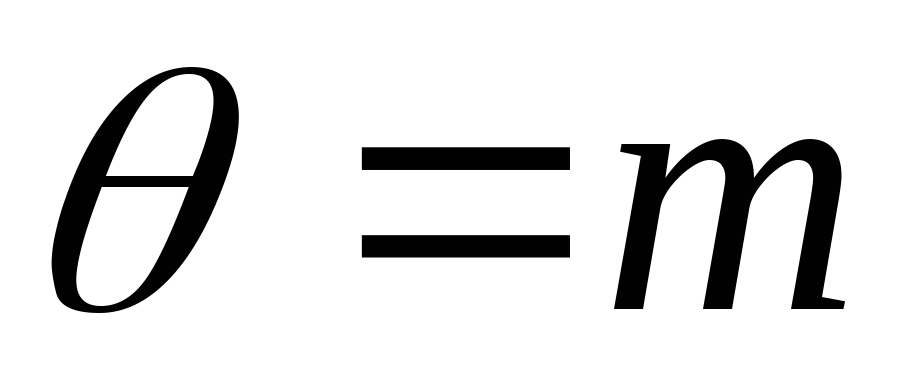 ,
имеем:
,
имеем: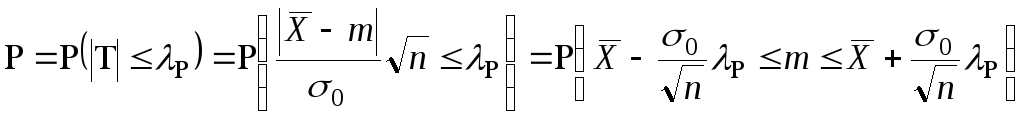 ,
где
,
где
 для заданного
для заданного
 находится по таблице нормального
распределения.
находится по таблице нормального
распределения.
Для ориентировки
приведем извлечение из таблицы нормального
распределения при наиболее употребительных
![]() .
.
-

0,9
0,95
0,99
0,9973

1,64
1,96
2,58
3
Пример6.![]() т.е.10,12,15,14,16,18,20,21,22.
Найдем доверительный интервал для
т.е.10,12,15,14,16,18,20,21,22.
Найдем доверительный интервал для
![]() при доверительной вероятности
при доверительной вероятности
![]() .
Тогда
.
Тогда
![]() =1,96,
=1,96,
![]() , и следовательно, доверительный интервал
примет вид:
, и следовательно, доверительный интервал
примет вид:
![]()
Пример5(продолжение).
Случай
б)
![]() -неизвестна.
-неизвестна.
Найдем
доверительный интервал для
![]() при
неизвестном
при
неизвестном
![]() .
Рассмотрим снова статистику
.
Рассмотрим снова статистику
![]() .
Поскольку
.
Поскольку
![]() неизвестно, заменим ее оценкой
неизвестно, заменим ее оценкой
![]()
![]()
Оказывается,
![]() имеет известное распределение Стьюдента
с
имеет известное распределение Стьюдента
с
![]() степенью свободы (это параметр статистики
степенью свободы (это параметр статистики
![]() )
или
)
или
![]() -распределения,
которое затабулировано.
-распределения,
которое затабулировано.
И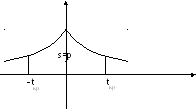 меем
меем
Исходя
из природы статистики (симметрия), имеем
![]() ,
где
,
где
![]() находится по таблице
находится по таблице
![]() -распределения,
поэтому
-распределения,
поэтому
![]() ,т.е.
,т.е.
![]() -доверительный
интервал для
-доверительный
интервал для
![]() при неизвестном
при неизвестном
![]() .
.
Пусть имеем 9 наблюдений: 5,7,2,3,4,8,10,11,12
![]()
![]()
Зададимся
теперь
![]() и найдем
и найдем
![]() по таблице
по таблице
![]() -распределения
при числе степеней свободы
-распределения
при числе степеней свободы
![]()
![]()
Тогда интервальная оценка будет иметь вид:
![]()
Аналогичным
образом, но с использованием других
статистик Т, строятся доверительные
интервалы для
![]() при: а)
при: а)![]() -неизвестно;
б)
-неизвестно;
б)![]() -неизвестно.
-неизвестно.
Замечание
2. Как уже упоминалось, статистический
анализ следует начинать с исключения
из результатов наблюдений неоднородных
(ошибочных) данных. Для этого применяют
"правило 3σ". Опишем его. Пусть
![]() - результат наблюдений. Найдем
- результат наблюдений. Найдем
![]() и
и
![]() и доверительный интервал
и доверительный интервал![]() ,
которому соответствует доверительная
вероятность
,
которому соответствует доверительная
вероятность
![]() .
Затем осуществим проверку:
.
Затем осуществим проверку:
![]() или нет. Если
или нет. Если
![]() ,
то
,
то
![]() исключают из выборки
исключают из выборки
![]() .
После просмотра всей выборки получаем
очищенную от неоднородностей выборку
.
После просмотра всей выборки получаем
очищенную от неоднородностей выборку
![]() ,
где
,
где
![]() .
Дальнейший статистический анализ
проводят с использованием этой выборки.
.
Дальнейший статистический анализ
проводят с использованием этой выборки.
