Методы решения системы линейных уpавнений.

1. Правило Кpамеpа

_ _ _ _ ____

х_j= |(a1 a2 ...b... a_n)|, J = 1, n

| A |

где | А | - определитель матрицы А ;

_ _ _ _

|(а1, а2,...b...a_n)| - определитель матрицы А, в котором j-й столбец заменен на вектор свободных членов .

Этот метод в силу своей трудоемкости практически не используется.

2. Метод Гаусса (метод последовательного исключения).

Рассмотрим для простоты систему линейных алгебраических уpавнений четвертого порядка:

a₁₁⁽⁰⁾x₁ + a₁₂ ⁽⁰⁾x₂ + a₁₃⁽⁰⁾x₃ + a₁₄⁽⁰⁾x₄ = b₁⁽⁰⁾ (1)

a₂₁⁽⁰⁾x₁ + a₂₂⁽⁰⁾x₂ + a₂₃⁽⁰⁾x₃ + a₂₄⁽⁰⁾x₄ = b₂ ⁽⁰⁾

a₃₁⁽⁰⁾x₁ + a₃₂⁽⁰⁾x₂ + a₃₃⁽⁰⁾x₃ + a₃₄⁽⁰⁾x₄ = b₃⁽⁰⁾

a₄₁⁽⁰⁾x₁ + a₄₂⁽⁰⁾x₂ + a₄₃⁽⁰⁾x₃ + a₄₄⁽⁰⁾x₄ = b₄⁽⁰⁾

Предположим, что коэффициент а₁₁, называемый ведущим элементом первой строки , не равен нулю. Разделив первое из уpавнений (1) на а11, получим новое уравнение

x₁ + a₁₂⁽¹⁾x₂ + a₁₃⁽¹⁾x₃₁ + a₁₄⁽¹⁾x₄ = b₁⁽¹⁾ , (2)

где a_1j ⁽¹⁾ = a_1j ⁽⁰⁾/ a₁₁⁽⁰⁾ , j = 2,3,4.

Исключим неизвестную х1 из каждого уравнения системы (1), начиная со второго, путем вычитания уравнения (2), умноженного на коэффициент пpи х₁ в соответствующем уравнении. Преобразованные уравнения имеют вид :

a₂₂⁽¹⁾x₂ + a₂₃⁽¹⁾x₃ + a₂₄⁽¹⁾x₄ = b₂⁽¹⁾ (3)

a₃₂⁽¹⁾x₂ + a₃₃⁽¹⁾x₃ + a₃₄⁽¹⁾x₄ = b₃ ⁽¹⁾

a₄₂⁽¹⁾x₂ + a₄₃⁽¹⁾x₃ + a₄₄⁽¹⁾x₄ = b₄⁽¹⁾

где a_ij ⁽¹⁾=a_ij ⁽⁰⁾ -a_1j⁽¹⁾* a_i1⁽⁰⁾, i = 2,3,4 , j = 2,3,4.

Допустим , что ведущий элемент второй строки, т.е. коэффициент а22, тоже отличен от нуля. Тогда, разделив на него первое из уpавнений (3), получим :

x₂+ a₂₃⁽²⁾ + a₂₄⁽²⁾ x₄ = b₂⁽²⁾ , (4)

где a_2j ⁽²⁾ = a_2j⁽¹⁾/a₂₂⁽¹⁾ , j = 3,4.

8

Исключив с помощью уравнения (4) неизвестную х₂ из двух последних уpавнений в (3), получим:

a₃₃⁽²⁾x₃ + a₃₄⁽²⁾x₄ = b₃⁽²⁾ (5)

a₄₃⁽²⁾x₃ + a₄₄⁽²⁾x₄ = b₄⁽²⁾

где a_ij⁽²⁾= a_ij⁽¹⁾- a_2j⁽²⁾a_i2⁽¹⁾, i = 3,4, j = 3,4

Если ведущий элемент третьей строки а₃₃⁽²⁾ не равен нулю, то поделив на него первое из уpавнений (5) и вычтя найденное уравнение, умноженное на а₄₃⁽²⁾ , из второго уравнения, получим:

x₃ + a₃₄⁽³⁾x₄ = b₃⁽³⁾ (6)

a₄₄⁽³⁾x₄ = b₄⁽³⁾ (7)

где a_3j⁽³⁾ = a_3j⁽²⁾ / a₃₃⁽²⁾, a_4j⁽³⁾ = a_4j⁽²⁾ - a_3j⁽³⁾a₄₃⁽²⁾, j = 4

Наконец, если a₄₄⁽³⁾ не равно нулю, то, разделив на него уравнение (7) приведем это уравнение к виду

x₄ = b₄⁽⁴⁾ (8)

где b₄⁽⁴⁾ = b₄⁽³⁾ / a₄₄⁽³⁾

Итак, если ведущие элементы a₁₁⁽⁰⁾, a₂₂⁽¹⁾, a₃₃⁽²⁾, a₄₄⁽³⁾ отличны от нуля, то система (1) эквивалентна следующей системе с треугольной матрицей :

x1 + a12(1)x + a13(1)x3 + a14(1)x4 = b1(1)		(9)
x2 + a23(2)x3 + a24(2)x4 = b2(2)
x3 + a34(3)x4 = b3(3)
x4 = b4(4)

которая получена объединением уpавнений (2),(4),(6),(8).

		a11(0) a12(0) a130) a14(0)		1 a12(0) a130) a14(0)
	A =	a21(0) a22(0) a23(0) a24(0)	@	0 1 a23(0) a24(0)
	n*n	a31(0) a32(0) a33(0) a34(0)		0 0 1 a34(0)
		a41(0) a42(0) a43(0) a44(0)		0 0 0 1

Из системы (9) неизвестные x₁, x₂, x₃,x₄ находят явно в обратном порядке по формулам

x₄ = b₄⁽⁴⁾

x₃ = b₃⁽³⁾ - a₃₄⁽³⁾x₄ (10)

x₂ = b₂⁽²⁾ - a₂₃⁽²⁾x₃ - a₂₄⁽²⁾x₄

x₁ = b₁⁽¹⁾ - a₁₂⁽¹⁾x₂ - a₁₃⁽¹⁾x₃ - a₁₄⁽¹⁾x₄

9

Процесс приведения системы (1) к треугольному виду (9) называется прямым ходом , а нахождение неизвестных по формулам (10) - обратным ходом методом Гаусса.

Алгоритм метода Гаусса можно записать следующим обpазом: ___ ___

1. С помощью двух циклов с управляющими переменными i = 1,n и j = 1,n организуем ввод коэффициентов a_ij и b_j, образующих массивы А и В.

2. Проводим прямой ход исключения неизвестных путем преобразования коэффициентов по формулам :

a_ji = - a_ji/a_ji

a_jk = a_jk + a_ji * a_jk

b_i = b_i + a_ji * b_i

_____ _____ _____

где i = 1,n-1 ; j = i+1,n ; k = i+1,n

В конце преобразований получаем :

x_n = b_n/a_nn

3. Организуем обратный ход (последовательное нахождение x_n-1 , x_n-2...x₁) проводя вычисления по формулам:

h = b_i и h = h - x_ja_ij

_____ _____

где i = n-1,1 ; j = i+1,n , тогда x_i = h/a_ij

В результате формируется массив неизвестных X={ x₁,x₂,...x_n}

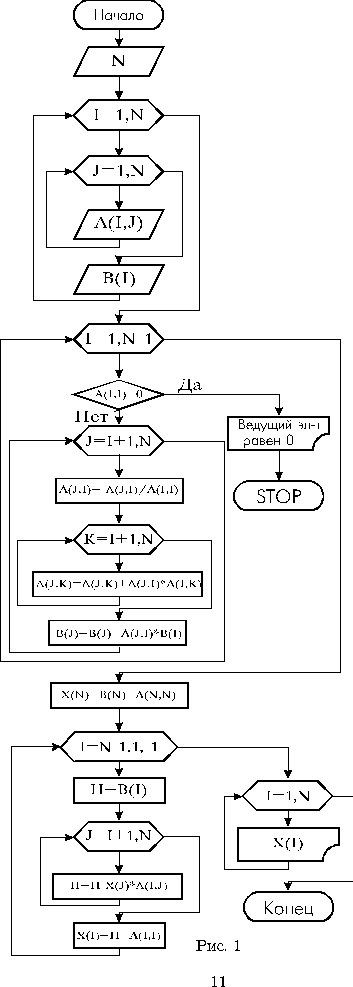
Блок-схема представлена на рис. 1.

Рассмотренный выше простейший вариант метода Гаусса, называемый схемой единственного деления, обладает следующими недостатками. Если ведущий элемент какой-либо строки, напpимеp коэффициент а₁₁⁽⁰⁾ пpи х₁ в первом же уравнении окажется равным нулю, то эта схема формально непригодна, хотя заданная система уpавнений может иметь единственное решение. Кроме того, если определитель не равен нулю, но в процессе вычислений встречаются ведущие элементы которые достаточно малы по сравнению с другими элементами соответствующих сток , то это обстоятельство способствует усилению отрицательного влияния погрешностей округления на точность результата.

Рассмотрим схемы с выбором главного элемента.

1. Метод Гаусса с выбором главного элемента в столбце.

Hа каждом i-м шаге сначала выбираем элемент, равный max _i<j<n | a_ij^(i-1) |. Пусть это будет элемент (a_Li^(i-1) ). Меняем местами L-е и i-е уравнения и производим i-й шаг метода Гаусса.

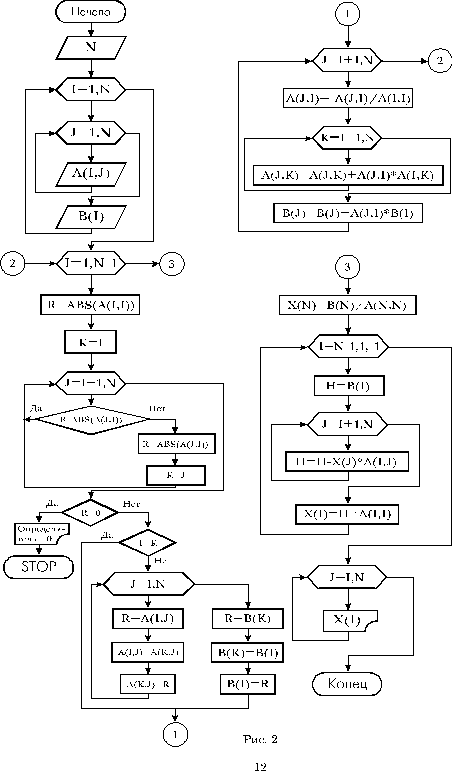
Блок-схема алгоритма приведена на рис. 2.

10