13.Теорема о сходимости монотонно ограниченной числовой последовательности

Теорема: Всякая монотонно убывающая и ограниченная снизу ч.п. имеет конечный предел.

Дано: {x_n } – Ограниченная снизу, строго убывающая ч.п.

Доказать: {x_n } – сходится.

Доказательство:

1. {x_n } – ограничена снизу, это значит, что множество её значений ограниченно снизу, а потому имеет точную нижнюю грань.

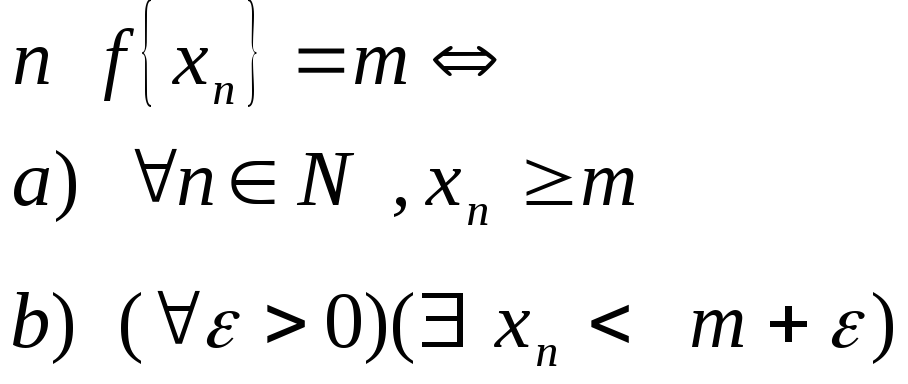
Геометрически это значит, что левее точки m членов данной последовательности нет, а в любой окрестности точки m в правой её части найдётся хотя бы один член данной последовательности.

2. {x_n } – строго убывает 

Из номеров n₁ и k выберем наибольший:

А)

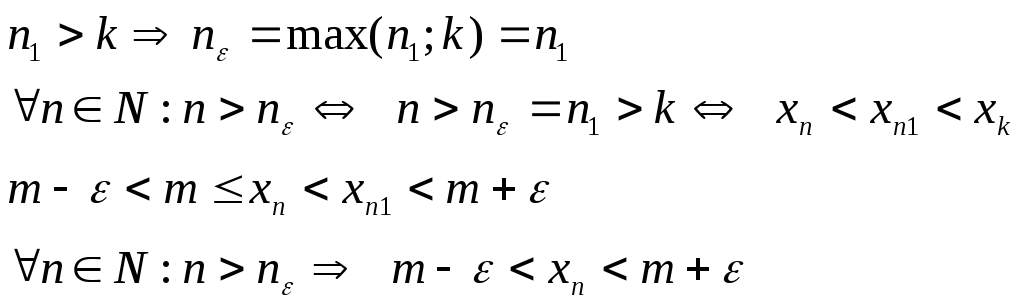
Б)

Из всего этого следует, что

Теорема для монотонно возрастающей функции доказывается аналогично.

14.Теоремы о пределе промежуточной последовательности.

Теорема о пределе промежуточной последовательности: если для любого n из множества натуральных чисел выполняется неравенство x_n≤y_n≤z_n , где {x_n},{y_n}, {z_n} это числовые последовательности, и существуют равные между собой пределы последовательностей {x_n} и {z_n}, то существует и предел промежуточной последовательности, равный предыдущему.

 nN: x_n≤y_n≤z_n, где {x_n},{y_n}, {z_n}-ч.п.

limx_n= limz_n=A, то limy_n=A

• Ч.п. называется сходящейся, если она имеет предел при n

Теорема о единственности предела сходящейся последовательности: если ч.п. имеет предел, то он единственный.

• Т.к. ч.п. определена как функция натурального аргумента, то для нее справедливы теоремы о пределах, доказанные для функции действительного переменного.

• В том числе верны теоремы об арифметических свойствах предела.

{x_n},{y_n}-ч.п.

lim x_n=A, lim y_n=B

тогда существуют пределы:

1)lim (c₁x_nc₂y_n)=c₁Ac₂B , где с₁ и с₂- const

2) lim (x_n·y_n)=A·B

3) lim (x_n/y_n)=A/B

Критерий Коши: для того, чтобы ч.п. была сходящейся необходимо и достаточно, чтобы для любого 0 существовал положительный натуральный номер n_, зависящий от  такой, что для любых n и k больших, чем n_ выполнялось неравенство x_n-x_k

Геометрически последнее неравенство означает, что с увеличением номеров членов последовательности расстояние между самими членами последовательности стремится к 0

lim x_n=A(0)( n_N)(n,kN:nn_,  kn_)x_n-x_k

верно и обратное!

15. Неравенство Бернулли. Число e и связанные с ним пределы.

1.Неравенство Бернулли.

Если число x ≥ -1, то для любого натурального n верно неравенство : (1+x)ⁿ ≥ 1+nx

Докажем это неравенство методом математической индукции.

1) в начале утверждение доказывается для n=1.

2)далее делается предположение индукции: предположим, что утверждение верно для некоторого номера n=k.

3)если удается доказать, что утверждение верно для следующего номера n=k+1, то можно утверждать, что оно верно для любого натурального номера.

Доказательство:

1)n=1, (1+x)ⁿ=1 - верно

2)n=2, (1+x)²≥1=+2x – верно

Предположим, что неравенство верно при (1+x)^k≥1+kx

(1+x)^k+1=(1+x)^k(1+x)=1+kx+x+kx²=1+(k+1)x

Для любого натурального n неравенство (1+x)ⁿ≥1+nx – верно, так как оно выполняется для n=k+1.

Рассмотрим неравенство Бернулли при x=1/n²(1+1/n²)ⁿ≥1+n

В случае n=1 неравенство переходит в равенство для всех n1 выполняется строгое неравенство.

2. Рассмотрим последовательность с общим членом (1+1/n)ⁿ= x_n, где n- множество натуральных чисел.

Докажем, что она имеет конечный предел. Для этого в начале рассмотрим вспомогательную последовательность.

x_n= (1+1/n)ⁿ⁺¹,nN

а)x_n/x_n-1=(1+1/n)ⁿ⁺¹/(1+1/n-1)ⁿ= (1-1/n²)ⁿ(1+1/n) (1-1/n²)ⁿ(1+1/n²)ⁿ=

Воспользуемся неравенством Бернулли

=(1-1/n⁴)ⁿx_n x_n-1- убывающая последовательность

x_n= (1+1/n)ⁿ⁺¹,nN - строго убывает

б) x_n= (1+1/n)ⁿ⁺¹,nN=4,27/8,64/27,…, (1+1/n)ⁿ⁺¹

Числовая последовательность ограничена снизу, так как ее члены не могут стать меньше одного.

Числовая последовательность (1+1/n)ⁿ⁺¹монотонно убывает и ограничена снизу, следовательно, она имеет предел. В качестве одной из нижних граней можно взять число один, но единица не является точной нижней гранью этой последовательности. Точной нижней гранью является наибольшая из всех нижних граней множества членов последовательности. Эту нижнюю грань обозначим e (infx_n=e), следующим пределом данной последовательности является число e.

Число e –иррациональное, e=2,718281…

3. x_n= (1+1/n)ⁿ,nN

lim_n(1+1/n)ⁿ⁺¹/1+1/n= lim_n(1+1/n)ⁿ⁺¹/ lim_n1+1/n=e/1= e lim_n(1+1/n)ⁿ⁺¹/1+1/n – существует и равен e.

Можно доказать, что lim_x(1+1/x)^x= e

1) lim_x(1+1/x)^x= e

2)1/x = zz0, x=1/z

3)ln(lim_x(1+1/x)^x)=lne

Под знаком предела стоит непрерывная функция, если искл. Из рассм. точкой x=0 по теореме о пределе непрерывной функции предел функции равен ее значению при предельном значении аргумента. На практике это значит, что знак функции и знак предела можно менять местами, так как логарифмическая функция непрерывна на своей области определения , верно равенство.

lim(x(ln_x+1)-lnx)=1

ln(lim_x(1+x)^1/x=lne

lim_x0(ln(1+x)^1/x)=1

15,Нера́венство Берну́лли утверждает: если , то

для всех

Доказательство проводится методом математической индукции по n.

При n = 0 неравенство, очевидно, верно.

Допустим, что оно верно для n, докажем его верность для n+1;

Неравенство справедливо также для вещественных (при )

Неравенство также справедливо для (при ), но указанное выше доказательство по индукции в случае не работает.

Число e может быть определено несколькими способами.

Через предел: (второй замечательный предел).

Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела