
Контрольная работа № 3
Контрольная работа № 3 состоит из пяти задач. Ниже подробно рассмотрены варианты решения заданий.
Образец выполнения задания № 11
Исследовать
функцию
![]() и начертить ее график.
и начертить ее график.
Решение.
1. Функция определена и непрерывна на
всей оси
![]() за исключением точек
за исключением точек
![]() и
и
![]() ,
в которых она имеет бесконечный разрыв.
,
в которых она имеет бесконечный разрыв.
2. Функция нечетна,
так как
![]() .
Ее график симметричен относительно
начала координат.
.
Ее график симметричен относительно
начала координат.
Это
позволяет ограничиться исследованием
графика данной функции только для
значений
![]() .
Остальную часть графика функции мы
построим, пользуясь его симметрией.
.
Остальную часть графика функции мы
построим, пользуясь его симметрией.
3. При
![]()
![]() ,
т.е. график функции проходит через начало
координат. Интервалы оси
,
т.е. график функции проходит через начало
координат. Интервалы оси
![]() ,
в которых функция сохраняет постоянный
знак, таковы:
,
в которых функция сохраняет постоянный
знак, таковы:
![]()
![]()
![]()
![]()
(здесь символическая; она указывает на знаки числителя и знаменателя рассматриваемой дроби).
4.
Вертикальной асимптотой графика функции
служит прямая
![]() ,
так как при
,
так как при
![]()
![]() .
.
Для того чтобы
выяснить, имеет ли график функции
невертикальные асимптоты, вспомним,
что коэффициенты
![]() и
и
![]() уравнения асимптоты
уравнения асимптоты
![]() находятся из соотношений
находятся из соотношений
![]() и
и
![]() .
.
Применим их к исследуемой функции:
![]()
Итак,
![]() Далее
Далее
![]()
![]() Следовательно,
Следовательно,
![]() .
.
Таким
образом, заключаем, что график исследуемой
функции имеет асимптоту с уравнением
![]() или
или
![]() .
Она (асимптота) проходит, как видим,
через начало координат и наклонена к
оси
.
Она (асимптота) проходит, как видим,
через начало координат и наклонена к
оси
![]() под углом в
под углом в
![]() .
.
Для
того чтобы судить о взаимоположении
графика и асимптоты относительно друг
друга, составляем
![]() ;
в нашем
;
в нашем
![]() Отсюда и определяем знак
Отсюда и определяем знак
![]() :
мы видим, что
:
мы видим, что
![]() при
при
![]() и
и
![]() либо при
либо при
![]() и
и
![]() .
.
Решение
этих систем показывает, что
![]() при
при
![]() .
Значит, для таких точек график будет
лежать над асимптотой.
.
Значит, для таких точек график будет
лежать над асимптотой.
Аналогичные
вычисления покажут, что
![]() при
при
![]() .
Следовательно, для этих значений
.
Следовательно, для этих значений
![]() график расположен снизу от асимптоты.
график расположен снизу от асимптоты.
5. Найдем интервалы возрастания и убывания функции и точки экстремума. Для этого вычисляем первую производную от данной функции:
![]() .
.
Найдем
стационарные точки. Для этого достаточно
приравнять к нулю числитель выражения
для производной. Решая уравнение
![]() ,
находим
,
находим
![]() ,
,
![]() ,
,
![]() .
Производная может менять знак при
прохождении аргумента
.
Производная может менять знак при
прохождении аргумента
![]() через эти точки и точки разрыва функции
через эти точки и точки разрыва функции
![]() и
и
![]() ,
в которых производная не существует.
,
в которых производная не существует.
Определим
знак производной в интервалах между
указанными точками. Так как
![]() и
и
![]() ,
то знак производной определяется знаком
разности
,
то знак производной определяется знаком
разности
![]() .
.
При
![]() имеем
имеем
![]() ;
следовательно, функция возрастает на
этом интервале.
;
следовательно, функция возрастает на
этом интервале.
При
![]() имеем
имеем
![]() ;
следовательно, функция убывает на этом
интервале.
;
следовательно, функция убывает на этом
интервале.
Отсюда
видно, что в точке
![]() функция имеет максимум (переход от
возрастания к убыванию).
функция имеет максимум (переход от
возрастания к убыванию).
Определим
ординату точки экстремума
![]() .
.
6.
Найдем интервалы выпуклости и вогнутости
графика функции и точки перегиба. Для
этого вычислим вторую производную
![]() .
Мы видим, что
.
Мы видим, что
![]() только при
только при
![]() .
Вторая производная может изменять знак
в этой точке и в точке разрыва функции
.
Вторая производная может изменять знак
в этой точке и в точке разрыва функции
![]() .
Определим знак второй производной в
интервалах между указанными точками.
.
Определим знак второй производной в
интервалах между указанными точками.
При
![]() имеем
имеем
![]() ;
следовательно, график функции вогнут.
;
следовательно, график функции вогнут.
При
![]() имеем
имеем
![]() ;
следовательно, график функции выпуклый.
Мы видим, что, проходя через точку
;
следовательно, график функции выпуклый.
Мы видим, что, проходя через точку
![]() ,
вторая производная меняет знак с минуса
на плюс. Следовательно,
,
вторая производная меняет знак с минуса
на плюс. Следовательно,
![]() - абсцисса точки перегиба. Так как при
- абсцисса точки перегиба. Так как при
![]()
![]() ,
то касательная к графику в точке перегиба
параллельна оси абсцисс.
,
то касательная к графику в точке перегиба
параллельна оси абсцисс.
7. Все результаты исследования мы используем для построения графика данной функции (рис.6). Вычерчивание графика следует начинать с нанесения на плоскость его асимптот, затем его точек, отвечающих точкам экстремума данной функции, и точек перегиба. Знание интервалов возрастания и убывания функции, а также интервалов выпуклости и вогнутости ее графика, помогут нам произвести вычерчивание графика осмысленно и точно.
Образец выполнения задания № 12
Дана
функция
![]() .
Найдите ее градиент в точке
.
Найдите ее градиент в точке
![]() по направлению линии
по направлению линии
![]() :
:
![]() .
.
Решение.
Градиент функции
![]() в произвольной точке
в произвольной точке
![]() вычисляется по формуле
вычисляется по формуле
![]() (1).
(1).
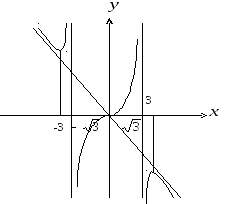
Рис. 7
Найдем его.
![]()
![]()
Найдем
эти значения в точке
![]() .
.
![]()
![]()
Отсюда получаем градиент в точке А по формуле (1).
![]()
Производная
функции
![]() в точке А по направлению вектора
в точке А по направлению вектора
![]() вычисляется по формуле
вычисляется по формуле
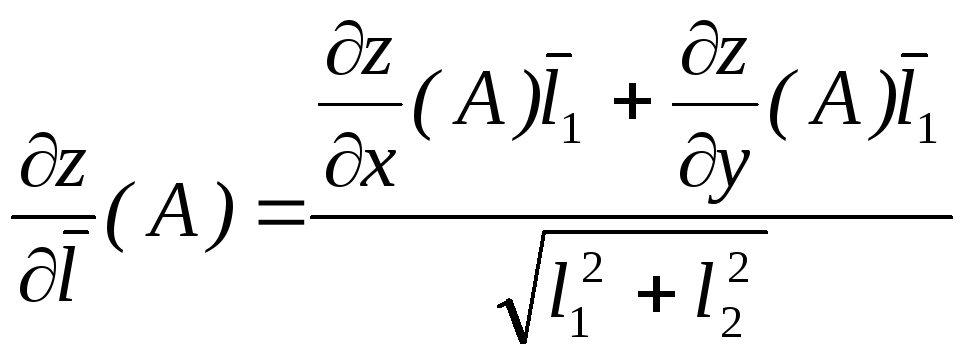 (2).
(2).
В данной задаче
![]() направлен по касательной к линии
направлен по касательной к линии
![]() в точке А (это и означает, что мы ищем
производную по направлению линии
в точке А (это и означает, что мы ищем
производную по направлению линии
![]() ,
см. рис. 7).
,
см. рис. 7).
В
общем случае, когда
![]() имеет уравнение
имеет уравнение
![]() ,
координаты касательного вектора
,
координаты касательного вектора
![]() в произвольной точке вычисляются по
формуле
в произвольной точке вычисляются по
формуле
![]()
(знак
![]() соответствует тому, что в точке А можно
нарисовать два противоположно –
направленных касательных вектора). В
нашей задаче
соответствует тому, что в точке А можно
нарисовать два противоположно –
направленных касательных вектора). В
нашей задаче
![]() :
:
![]() ,
поэтому
,
поэтому
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
В
точке А эти значения получаются такими
![]()
![]() .
.
Отсюда
![]() .
.
Давайте
укоротим этот вектор в 12 раз; координаты
остаются целыми
![]() ,
но дальнейшие вычисления упростятся.
По формуле (2) получаем
,
но дальнейшие вычисления упростятся.
По формуле (2) получаем
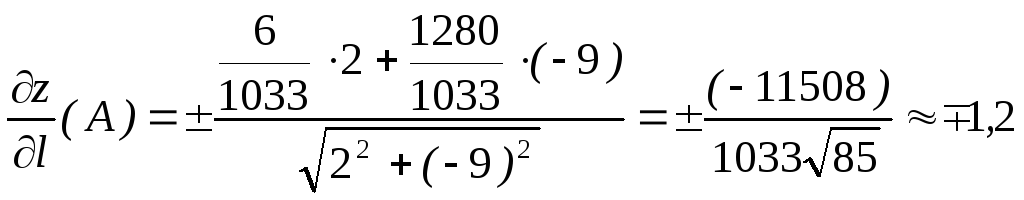 .
.
Если
мы хотим найти
производную в сторону возрастания
координаты х, то должно быть
![]() .
В нашей задаче это получится, если у
.
В нашей задаче это получится, если у
![]() взять знак +, так как тогда
взять знак +, так как тогда
![]() ,
,
![]() Выбрав таким образом верхний знак,
получим
Выбрав таким образом верхний знак,
получим
![]() .
.
Образец выполнения задания № 13
Алгоритм
исследования функции
![]() на экстремум.
на экстремум.
1) Проверить необходимое условие экстремума:
-
Найти частные производные первого порядка
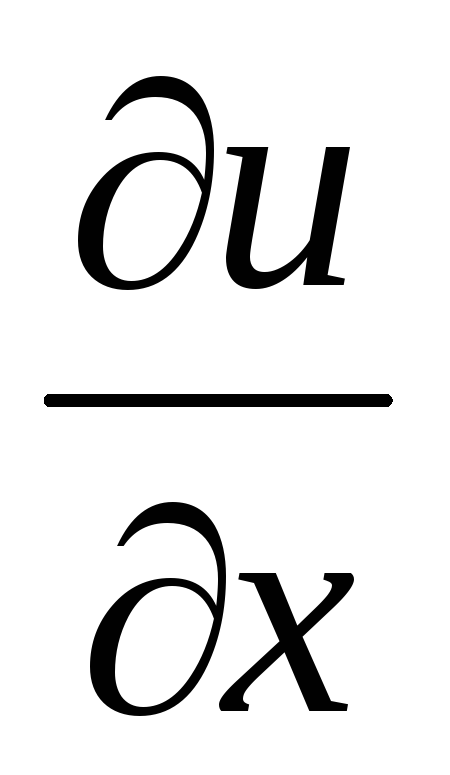 ,
,
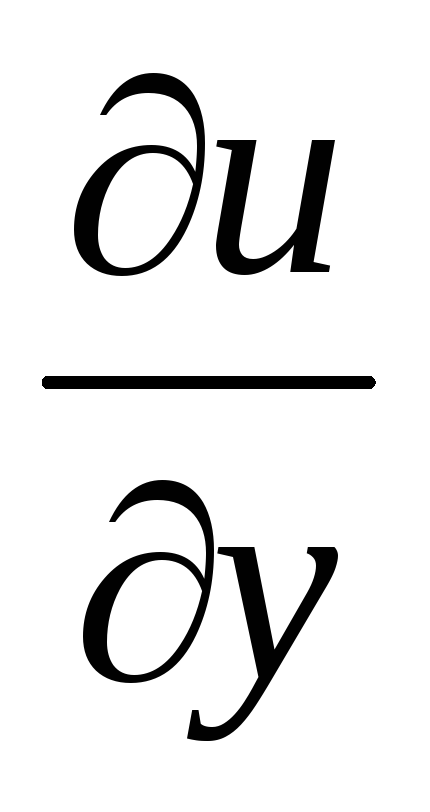 .
. -
Решив систему уравнений
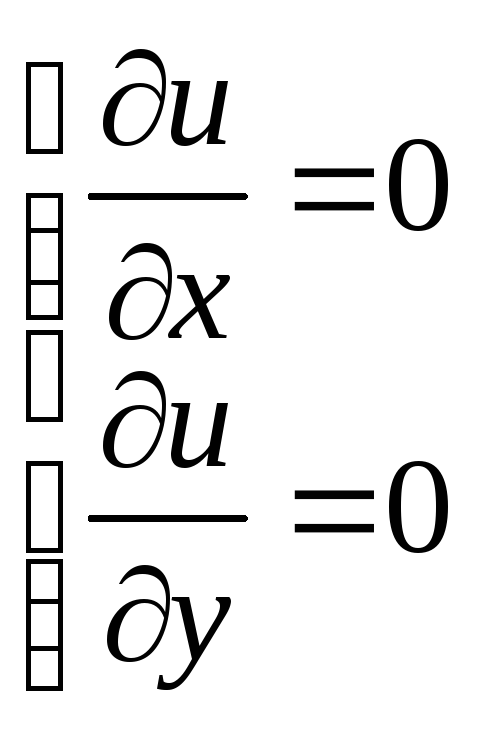 ,
найти точки возможного экстремума.
,
найти точки возможного экстремума.
2) Проверить достаточные условия экстремума.
-
Найти частные производные второго порядка
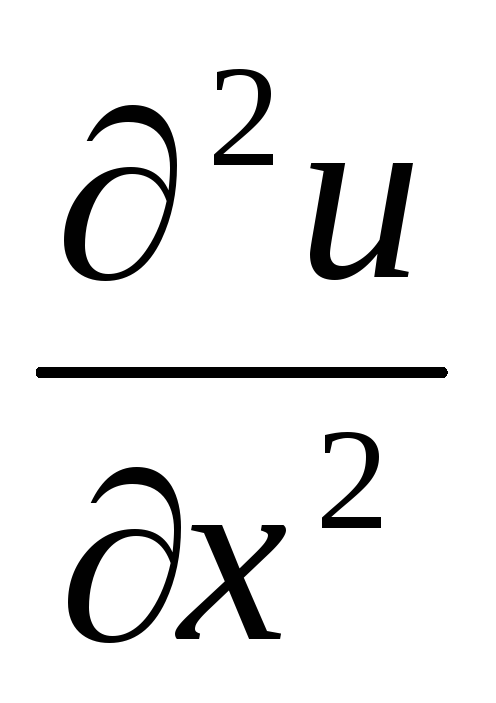 ,
,
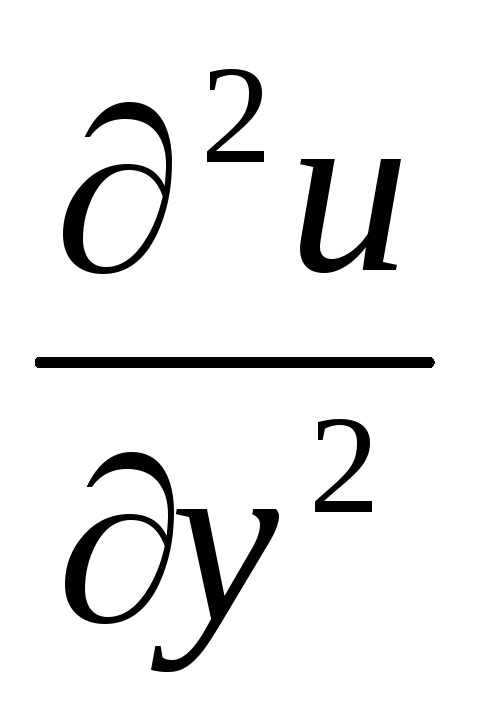 ,
,
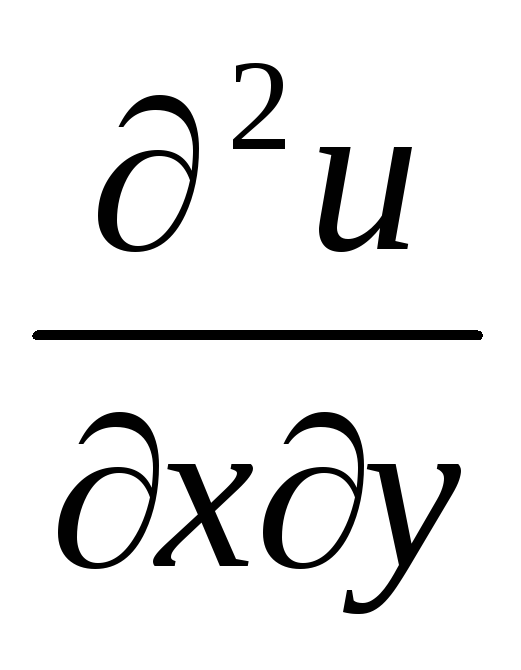 .
. -
Составить матрицу
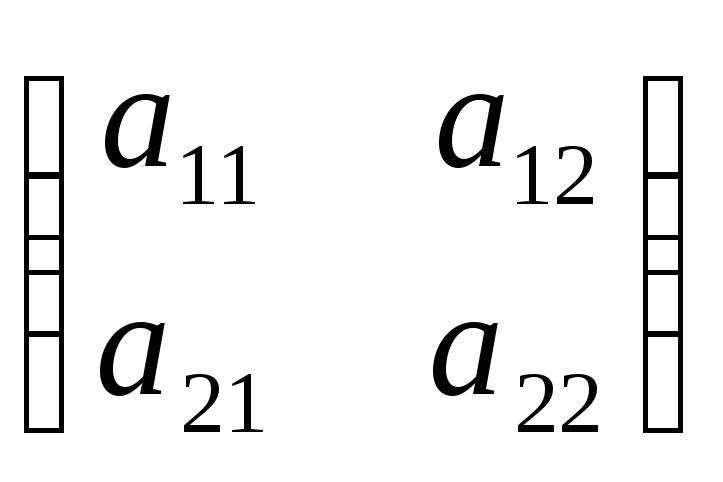 ,
где
,
где
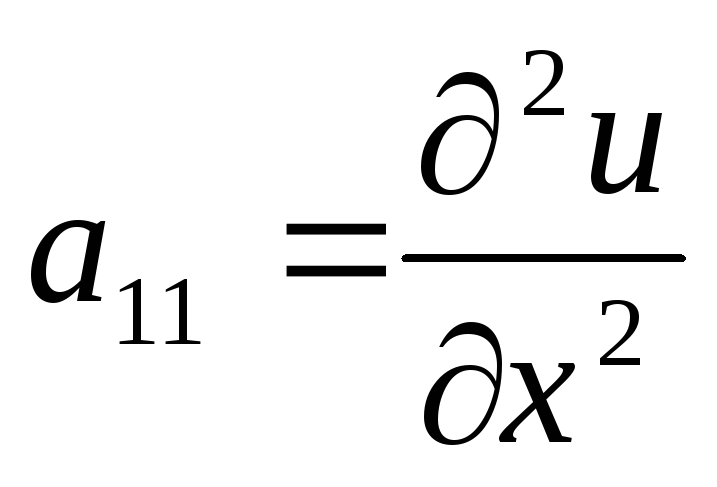 ,
,
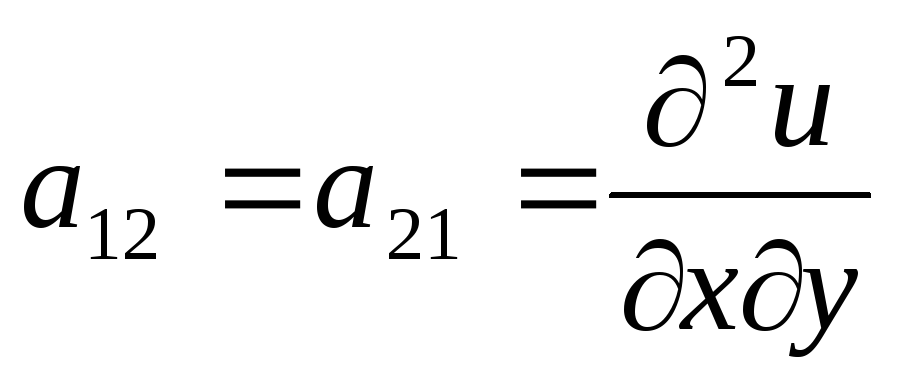 ,
,
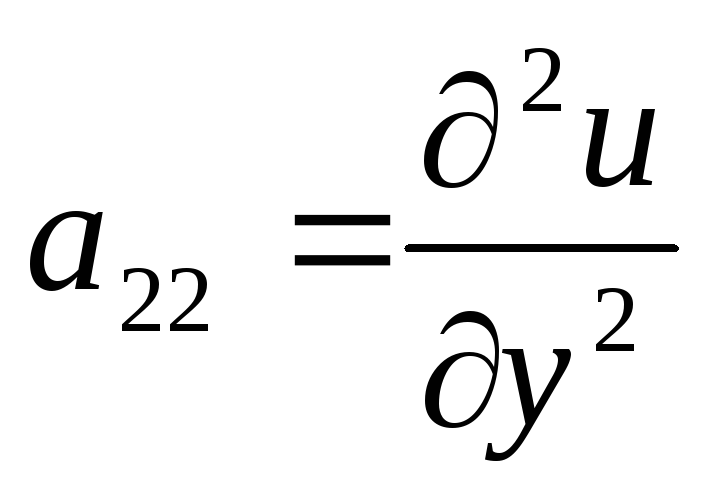 ,
,
и найти
![]() .
.
-
Вычислить
 в точках возможного экстремума. Если
в точках возможного экстремума. Если
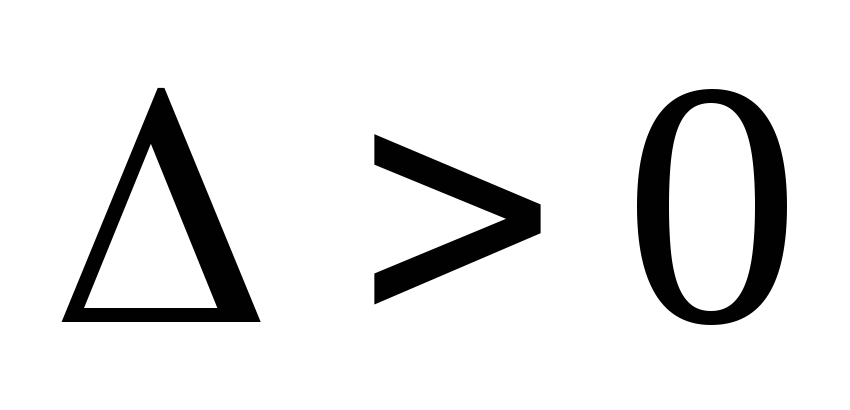 ,
то в данной точке функция имеет экстремум,
а именно – максимум при
,
то в данной точке функция имеет экстремум,
а именно – максимум при
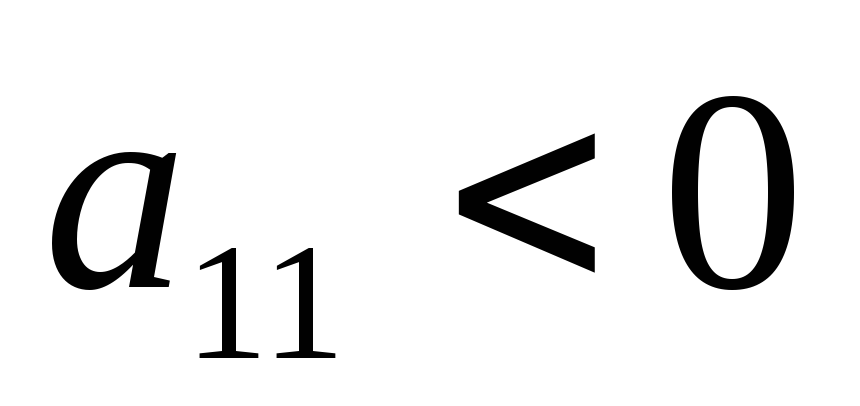 (или
(или
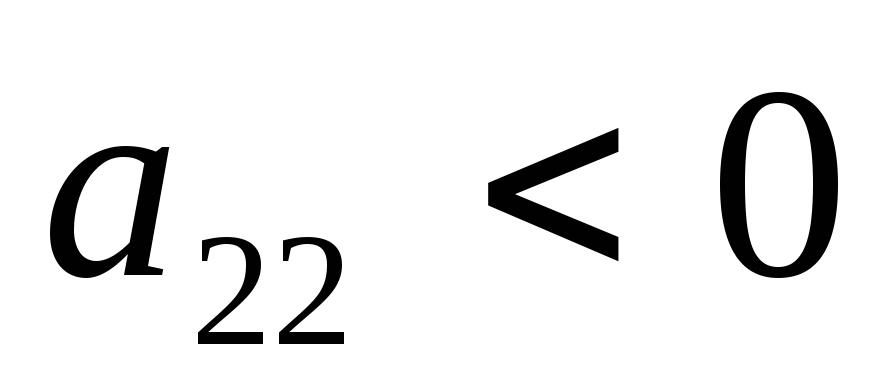 )
и минимум при
)
и минимум при
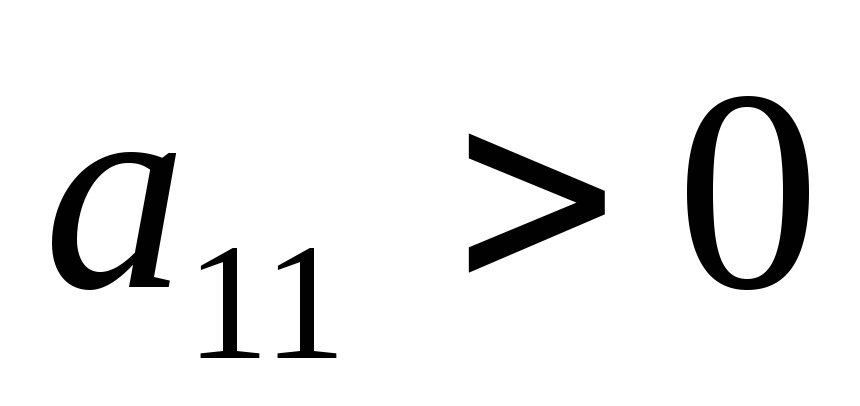 (или
(или
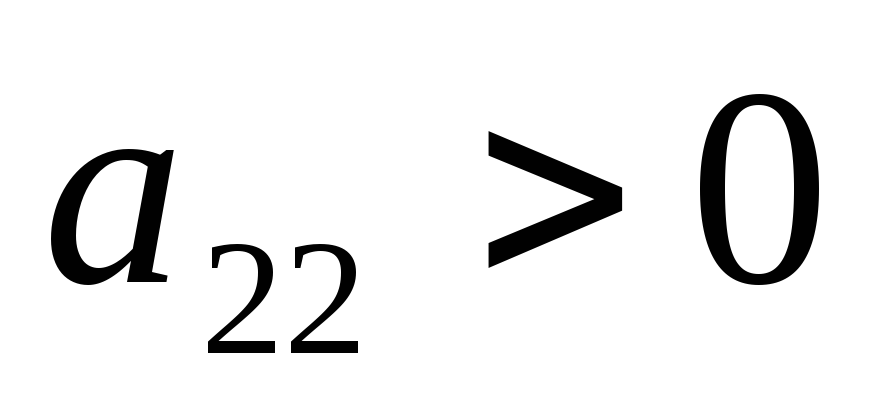 );
если
);
если
 ,
то в данной точке экстремума нет; если
,
то в данной точке экстремума нет; если
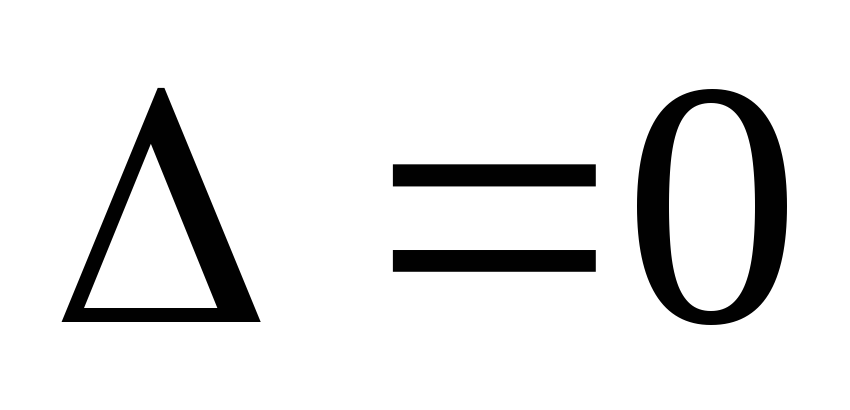 ,
то требуется дальнейшее исследование.
,
то требуется дальнейшее исследование.
Образец выполнения задания № 14
Найти
частные производные второго порядка и
дифференциал функции
![]() .
.
Решение:
Сначала находим частные производные
первого порядка
![]() ,
,
![]() .
Затем вычисляем частные производные
от частных производных первого порядка.
.
Затем вычисляем частные производные
от частных производных первого порядка.
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
