Алгоритм нахождения частного решения уравнения п-го порядка с постоянными коэффициентами методом вариации произвольных постоянных (метод Лагранжа)

1. Решить однородное уравнение, соответствующее неоднородному уравнению (54). Полученное решение записать в виде:

.

Где - фундаментальная система решений однородного уравнения.

2. Выписать структуру частного решения неоднородного уравнения в виде:

.

3. Записать систему (42) для определения функций .

4. Путем интегрирования найти функции (произвольные постоянные, возникающие при интегрировании, положить равными нулю).

5. Полученные функции , подставить в выражение для , которое и будет частным решением неоднородного уравнения (54).

Пример 25. Найти частное и общее решение уравнения:

.

▲ В соответствии с методом Лагранжа, составим соответствующее этому неоднородному уравнению с постоянными коэффициентами однородное уравнение

и решим его. Для этого запишем характеристическое уравнение: . Это характеристическое уравнение имеет корни: .

Мы видим, что корни характеристического уравнения комплексные, поэтому общее решение однородного уравнения имеет вид:

.

Будем искать частное решение исходного уравнения в виде

. (*)

Составим систему (42)

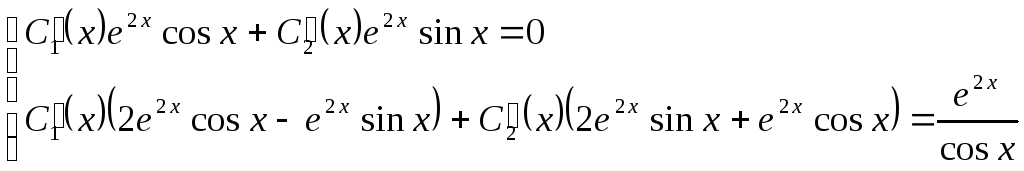
или сокращая на е^2х,

. (**)

Решить эту систему относительно можно различными способами, например, используя правило Крамера. В данном случае удобнее сначала преобразовать второе уравнение, а именно, умножить обе его части первого уравнения на –2 и затем прибавить полученный результат ко второму. В итоге получим уравнение:

и, следовательно, этим уравнением можно заменить второе уравнение в системе (**)

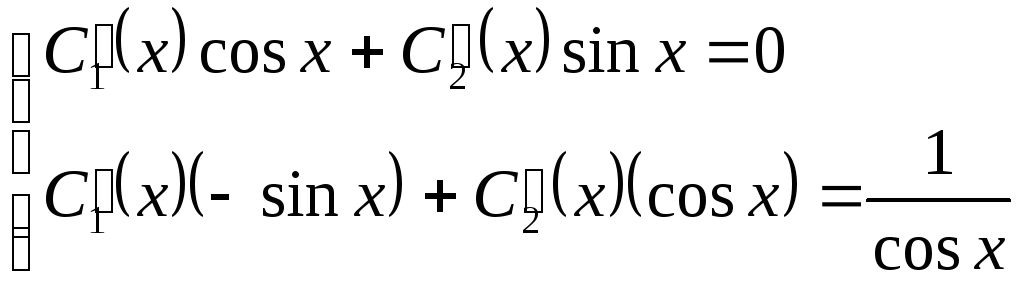
Решая эту систему по правилу Крамера, получим

.

Подставляя полученные значения в (*), получим частное решение исходного неоднородного уравнения

.

Таким образом, общее решение исходного уравнения имеет вид:

.▲

2. Другой метод нахождения частного решения неоднородного уравнения с постоянными коэффициентами является так называемый метод подбора или метод неопределенных коэффициентов. Этот метод основан на том, что структура частного решения неоднородного линейного уравнения п-го порядка (54) в некоторых случаях повторяет структуру правой части, то есть определяется видом функции . Это случаи, когда можно представить в виде комбинаций основных функций: многочленов, показательной и тригонометрических функций. Точнее говоря, метод неопределенных коэффициентов применим к функциям специального вида, то есть к функциям, которые можно записать следующим образом:

, (55)

где R_q(x), P_l(x) – многочлены переменной х степени q и l соответственно;  - заданные действительные числа.

Итак, если правая часть уравнения (54) имеет вид (55), то частное решение этого уравнения подбирается в виде:

, (56)

где т = max (q,l); Q_m(x), T_m(x) – многочлены переменной х степени т с неопределенными коэффициентами и определяются следующим образом:

(57)

где - неопределенные коэффициенты, которые необходимо определить; а натуральное число s в формуле (56) определяется так:

Таким образом, по корням характеристического уравнения и виду правой части можно указать вид частного решения неоднородного уравнения с постоянными коэффициентами.