5. Примеры разложения элементарных функций в степенные ряды.

Рассмотрим разложения в ряд Маклорена некоторых элементар­ных функций.

Разложение функции . Имеем: , откуда при получаем: . По формуле (10) для функ­ции составим ряд Маклорена:

(13)

Найдем интервал сходимости ряда (13)

..

Следовательно, ряд абсолютно сходится на всей числовой прямой.

Докажем теперь, что функция — сумма ряда (13).

Отметим, что в силу необходимого условия сходимости ряда для любого х справедливо равенство

. (14)

Так как , то

,

где . Отсюда, учитывая, что , получаем

.

Так как в силу (14)

, то и .

Поэтому, переходя к пределу в последнем неравенстве при , получаем, что при любом х, и, следовательно, функция является суммой ряда (13).

Таким образом, при любом х имеет место разложение

Разложение функции . Имеем:

(см. гл. 5, § 10, п. 2), откуда, полагая , получаем: Составим по фор­муле (10) для функции sin х ряд Маклорена:

Легко проверить, что полученный ряд сходится абсолютно на всей числовой прямой. Исследуем остаточный член

,

где. Так как , то . В силу (14) . Следовательно, при любом х. А это означает, что функция sin х является суммой построенного ряда, т. е. имеет место разложение

Разложение функции . Аналогично пре­дыдущему, можно получить разложение функции cos х в ряд Мак­лорена, справедливое при любом х. Однако еще проще разложение cos х получается почленным дифферецированием ряда для sin х:

,

откуда

Кроме рассмотренных функций е^х, sin x, cos х в ряд Маклорена могут быть разложены и многие другие функции. Вместо ряда Маклорена можно было бы рассмотреть более общий ряд Тейлора по степеням (х — а), где , т. е. ряд вида

Все изложенное полностью переносится и на эти ряды.

При разложении функции cos x в ряд Маклорена было использо­вано свойство почленно дифференцируемости степенных рядов. Аналогично можно использовать и другое свойство степенных ря­дов — их почленную интегрируемость. В качестве примера разло­жим с помощью почленного интегрирования в степенные ряды функции и arctg x.

Рассмотрим ряд Данный ряд является геометрической прогрессией, первый член которой равен единице, а знаменатель q = x. Как известно, при данный ряд сходится и его сумма равна . Следовательно,

(15)

Равенство (15) является разложением функции в сте­пенной ряд.

Подставляя в равенство (15) —t вместо х, получаем

равенство

,

справедливое при . Проинтегрируем этот степенной ряд почленно в пределах от 0 до х (). Имеем

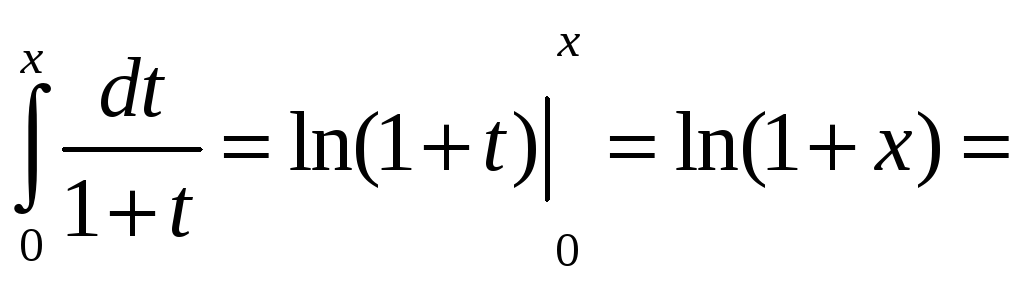
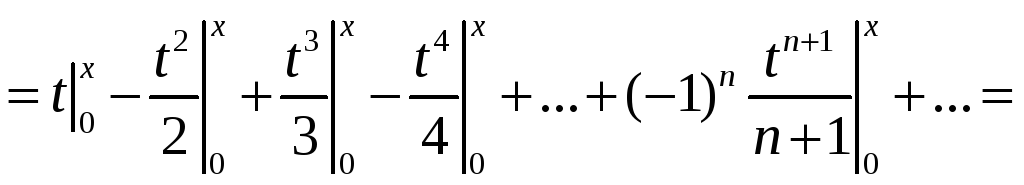
Отсюда

(16)

Равенство (16) является разложением функции в степен­ной ряд. Оно справедливо при . Можно доказать, что это равенство верно и для .

Действительно, при х= 1 левая часть (16) равна ln 2, а правая часть — сходящийся по признаку Лейбница числовой ряд

(17)

Остается проверить справедливость равенства

(18)

Для этого проинтегрируем от 0 до 1 выражение

,

полученное в результате деления единицы на . Имеем

,

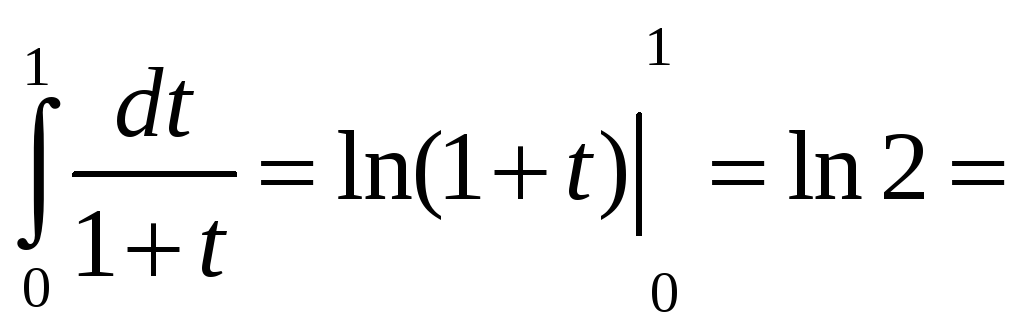
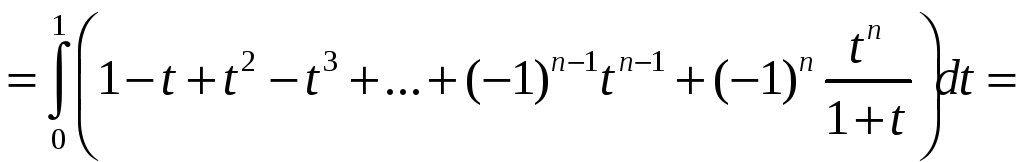
т.е. . (19)

В этом равенстве сумма первых п слагаемых является частичной суммой ряда (17). Запишем (19) в виде

. (20)

Так как при , то

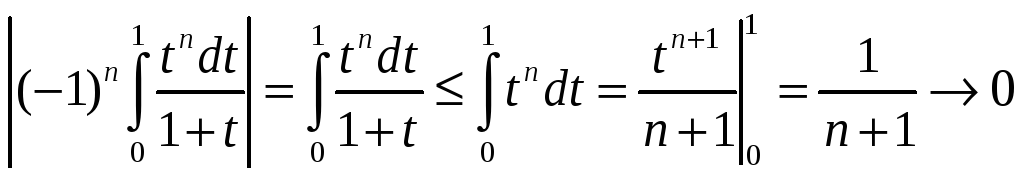при .

Отсюда заключаем, что интеграл в правой части (20) стремится к нулю при , следовательно, , что и означает справедливость равенства (18). Найдем теперь разложение функции arctg x. Подставляя в (15) — t² вместо х и интегрируя по от 0 до х, имеем

(21)

Равенство (21) справедливо при . Однако аналогично предыдущему можно показать, что оно верно и для .

В заключение отметим, что степенные ряды имеют разнообраз­ные приложения. С их помощью с любой заданной точностью вы-

числяют значения функций (в частности, значения и ); находят приближенные значения определенных интегралов, которые или не выражаются через элементарные функции, или сложны для вычислений. Так, например, интеграл не берется в элементарных функциях, поскольку первообразная функции не

является элементарной. В то же время эта первообразная легко выражается в виде степенного ряда. Действительно, так как , то, умножая этот ряд на , получаем

,

причем последний ряд сходится при любом . Интегрируя его почленно от 0 до , имеем

С помощью этого равенства можно при любом а с любой степенью точности вычислить данный интеграл.

Наконец, значительную роль играют степенные ряды в прибли­женных методах решений дифференциальных уравнений.

Контрольные вопросы