- •Раздел 3. Основы теории конечных автоматов
- •3.1. Логические функции
- •3.2. Примеры логических функций
- •3.2. Связь логических функций и функциональных схем
- •3.3. Каноническое представление логических функций
- •3.4. Задача минимизации логических функций
- •3.5. Основные понятия теории конечных автоматов
- •1) Для любой входной буквы ai имеется ребро, выходящее из qi , на котором написано aj (условие полноты);
- •2) Любая буква aj встречается только на одном ребре, выходящем из qi (условие непротиворечивости или детерминированности).
- •1) ( Qi , aj ) задается автоматной таблицей s;
- •2) Для любого слова а* и любой буквы аj
- •3.6. Абстрактная и структурная теория конечных автоматов
- •3.6. Сопоставимость конечных автоматов
- •3.7. Синхронные сети из автоматов.
- •1. Параллельное соединение (рис. 3.11). Различаются соединения с общими и раздельными входами (алфавитами).
- •3.8. Пример синтеза конечного автомата
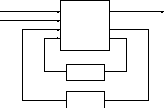
- •X(n) (состояние / выход)
- •Преобразуем исходную таблицу в специальную форму с выделением входных - выходных сигналов и внутренних состояний.
- •X1(n) Комб. Y(n)
- •3.9. Программная реализация логических функций и автоматов.
1. Параллельное соединение (рис. 3.11). Различаются соединения с общими и раздельными входами (алфавитами).


S1
S1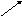 А1
V1
V1
А1
V1
V1


 A
A
S2
S2
 A2
A2


 V2
V2
V2
V2
Рис. 3.11 - Параллельное соединение автоматов
Для случая, когда параллельное соединение автоматов представлено парой автоматов S1 = {A1, Q1, V1, 1, 1}; S2 = {A2, Q2, V2, 2, 2} то его можно рассматривать как один автомат S = {A, Q, V, , }, который определяется следующим образом: A = A1A2, Q = Q1Q2, V = V1V2. Таким образом, входной символ автомата S - это пара символов: a = (a1, a2), состояние автомата S - это пара состояний: q = (q1, q2), где q1 Q1, q2 Q2. Далее (q, a) = ((q1, q2), (a1, a2)) = (1(q1, a1), 2(q2, a2)), т.е. смена состояний происходит независимо и одновременно. Аналогично: (q, a) = (1(q1, a1), 2(q2, a2)) = (v1, v2), где v1 V1; v2 V2. При этом автомат S называется прямым произведением автоматов S1 и S2.
Для второго варианта параллельного соединения входные алфавиты S1, S2 и S совпадают. Поэтому (q, a) = (1(q1, a), 2(q2, a)).
Последовательное соединение автоматов показано на рис. 3.12.
S1
S2


 A1 A2=V1
V2
A1 A2=V1
V2
Рис. 3.12 - Последовательное соединение автоматов
Эту сеть можно описать как автомат S = {A, Q, V, , }, причем A=A1, V=V2, V1=A2 и Q = Q1 Q2. Для определения и существенна задержка функции 1. Если задержка 1 равна нулю, то
1(q1(t), a(t)) = V1(t);
q(t+1) = (q1 (t+1), q2(t+1)) =
= (1(q1(t), a(t)), 2(q2(t), 1(q1(t), a(t)))).
Выражение в левой части зависит только от q(t) и a(t) и, следовательно, определяет q(t+1) как функцию от этих переменных. Эта функция и есть функция для S.
Если же время задержки 1 равно единице, то получим:
1(q1(t), a(t)) = V1(t+1);
q(t+1) = (1(q1(t), a(t)), 2(q2(t), 1(q1(t-1), a(t-1)))).
Таким образом, зависимость только от предыдущего такта не получается и необходимо усложнять автоматное описание такой сети.
Методы получения единого автоматного описания для сетей из автоматов называются методами композиции автоматов. Эти методы решают задачу анализа сетей, поскольку исследование поведения сетей удобно проводить при наличии автоматного описания: таблицы переходов или графа переходов.
3.8. Пример синтеза конечного автомата
Пусть конечный автомат задан совмещенной таблицей переходов - выходов.
Таблица переходов-выходов КA.
X(n) (состояние / выход)
y(m) 0 1 2 3
-
0
2/0
2/0
0/0
0/1
1
1/1
1/0
0/1
1/1
2
1/0
0/1
2/1
0/0
Преобразуем исходную таблицу в специальную форму с выделением входных - выходных сигналов и внутренних состояний.
Таблица 3.11 - Промежуточная таблица
|
Входы |
x(n) |
000 111 222 333 |
|
Текущие состояния |
s(n) |
012 012 012 012 |
|
Следующие состояния |
s(n+1) |
211 210 002 010 |
|
Выходы |
y(n) |
010 001 011 110 |
Заменяя десятичные числа на двоичные, получим таблицу истинности, в которой значения x(n), s(n), s(n+1), y(n) представлены в двоичном коде.
Таблица 3.12 - Таблица истинности конечного автомата
|
x(n) |
s(n) |
s(n+1) |
y(n) | |||
|
x1(n) |
x2(n) |
s1(n) |
s2(n) |
s1(n+1) |
s2(n+1) |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
* |
* |
* |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
* |
* |
* |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
* |
* |
* |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
* |
* |
* |
Граф конечного автомата будет иметь вид, показанный на рис. 3.13.

 0/1
1/0
3/1
0/1
1/0
3/1

 2/1
1
2/1
1



 0
1/1
3/0 0/0
0
1/1
3/0 0/0
2


 /0
3/1
/0
3/1
 0/0
0/1 2 2/1
0/0
0/1 2 2/1
Рис. 3.13 - Граф синтезируемого конечного автомата
Исходные функции для синтеза автомата по таблице 3.12 будет иметь вид:
s1(n+1) = x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n);
s2(n+1) = x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n)
x1(n)x2(n)s1(n)s2(n);
y(n) = x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n)
x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n).
Минимизируем данные функции с помощью карт Карно.
Для s1(n+1).
 x1(n)x2(n)
x1(n)x2(n)
s1(n)s2(n) 00 01 11 10
-

 00
001
1
01
11
10
1
Для s2(n+1).
 x1(n)x2(n)
x1(n)x2(n)
s1(n)s2(n) 00 01 11 10
-
 00
00 01
011
1
1
11
10
1
Для y(n).
 x1(n)x2(n)
x1(n)x2(n)
s1(n)s2(n) 00 01 11 10
-

 00
001

 01
011
1
1
11
10
1
1
Результаты минимизации представим в виде:
s1(n+1) = x1(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n);
s2(n+1) = x1(n)s1(n)s2(n) x1(n)x2(n)s1(n)s2(n)
x1(n)x2(n)s1(n)s2(n);
y(n)=x2(n)s1(n)s2(n) x1(n)x2(n)s1(n) x1(n)x2(n)s1(n)s2(n)
x1(n)x2(n)s1(n)s2(n).
Структура автомата в общем виде представлена на следующем рис. 3.14.