Вычисление характеристик рядов распределения

Описательная статистика охватывает методы описания статистических данных, представления их в форме рядов распределений.

Условно все характеристики рядов распределения можно разделить на четыре группы:

1. Показатели, характеризующие закон распределения.

2. Показатели, характеризующие центральную тенденцию (меры среднего уровня).

3. Показатели (меры), характеризующие рассеяние относительно центральной тенденции.

4. Показатели асимметрии.

Рассмотрим их подробнее.

Показатели, характеризующие закон распределения. Это, прежде всего, уже знакомые нам частоты и проценты, а также накопленные частоты и проценты.

Как для абсолютных, так и для относительных частот можно определить кумулятивные показатели – накопленные частоты и проценты, которые рассчитывается путем суммирования всех частот (процентов) до выбранной категории включительно.

Упомянем также квартили, разбивающие ранжированный ряд значений признака на 4 части по 25% значений в каждой. Квартили при этом называются нижней, средней и верхней (при этом, очевидно, средняя квартиль совпадает с медианой). Аналогично можно ввести децили, разбивающие вариационный ряд значений на группы по 10% чисел и другие квантили – числа, разбивающие упорядоченную совокупность значений признака на равные по объему части.

Показатели, характеризующие центральную тенденцию (меры среднего уровня). Среднее арифметическое представляет собой количественную характеристику качественно однородной совокупности. Наиболее распространенными средними являются средняя арифметическая, мода и медиана.

Среднее арифметическое () – обобщающий показатель, выражающий типичные размеры количественных признаков качественно однородных явлений, определяется по формуле:

,

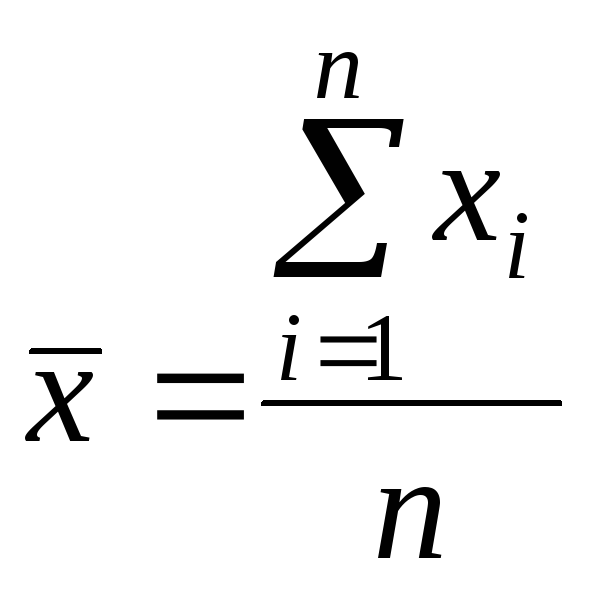где x_i – варианта с порядковым номером (=1,…n); n – объем совокупности.

Для интервального ряда используется средняя арифметическая взвешенная:

,

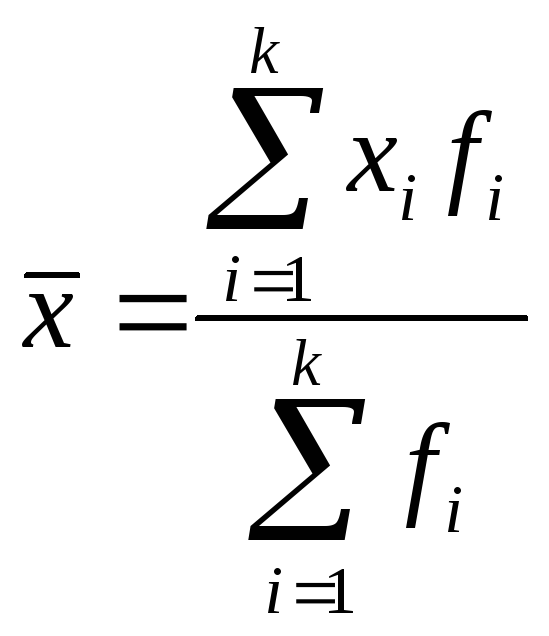где f_i – частота индивидуального значения признака;

k – количество градаций признака.

Мода () – варианта, которая чаще всего встречается в данном упорядоченном ряду. Если таких вариант несколько, то берется первая из них в упорядоченном ряду.

Пример. Ряд: 4,5,5,6,6,7. В данном ряду мода число 5.

В интервальном ряду по определению можно установить только модальный интервал, при этом значение моды определяется по формуле:

,

где x₀ – нижняя граница модального интервала;

      l – величина интервала;

      f _μo – частота модального интервала;

     f _μo–1 – частота предмодального интервала;

    f _μo+1 – частота послемодального интервала.

Медиана () – варианта, находящаяся в середине упорядоченного ряда:

=, если число вариант нечетно (n=2m+1);

=, если число вариант четно (n=2m).

Пример. Ряд: 4,5,5,6,6,7. Медиана равна 5,5 (ряд четный).

Ряд: 4,5,5,6,6,7,8. Медиана равна 6 (ряд нечетный).

Медиана используется, когда изучаемая совокупность неоднородна. Особое значение она приобретает при анализе асимметричных рядов – она дает более верное представление о среднем значении признака, т.к. не столь чувствительна к крайним (нетипичным в плане постановки задачи) значениям, как средняя арифметическая.

Для интервального ряда можно определить как медианный интервал, а сама медиана рассчитывается по формуле:

,

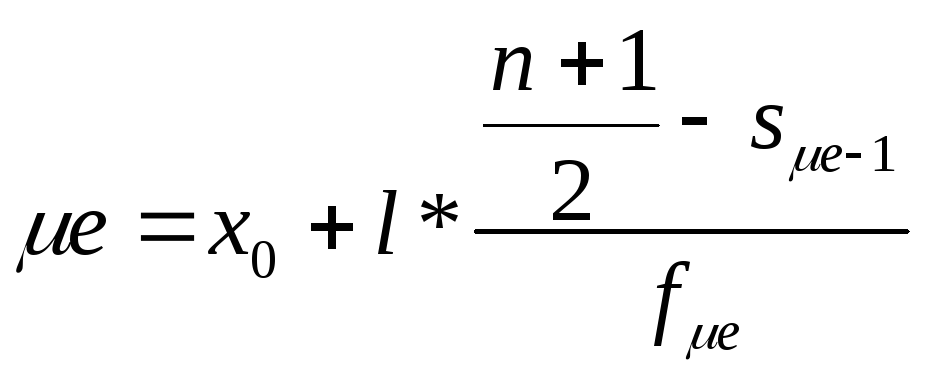где x₀ – нижняя граница медианного интервала;

l – величина интервала;

n – количество единиц в совокупности;

s _μe–1 – накопленная частота предмедианного интервала;

f _μe – частота медианного интервала.

Пример. Выборка результатов контрольного тестирования дала следующий интервальный ряд (табл.6)

Таблица 6

Интервальный ряд по результатам тестирования

Интервалы баллов	До 70	70–80%	80–90%	90-100%
Частота	10	25	40	20

Определим среднее арифметическое и моду, медиану по выборке.

1. Рассчитаем выборочную среднюю

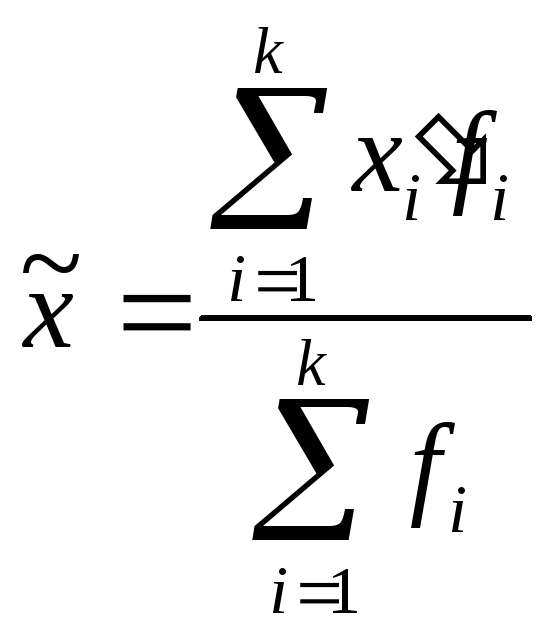
(см. расчетную табл. 7)

Таблица 7

Расчетная таблица

xi	fi	xi' (середины интервалов)	xi'*fi
60-70	10	65	650
70-80	25	75	1875
80-90	40	85	3400
90-100	20	95	1900
Итого Σ	95		7825

2. Вычислим моду. Для этого сначала определим модальный интервал (интервал с наибольшей частотой). В нашем примере это интервал 80-90% с частотой равной 40.

Исходя из этого легко определить необходимые величины:

x₀ =80;

l = 10;

      f _μo = 40;

     f _μo–1 =25;

    f _μo+1 =20.

Подставляем в формулу найденные значения для расчета моды интервального ряда:

.

2. Вычислим медиану. Для определения медианного интервала необходимо создать ряд накопленных частот (табл. 8):

Таблица 8

Расчетная таблица

Интервалы баллов	До 70	70–80%	80–90%	90-100%
Частота	10	25	40	20
Накопленные частоты	10	10+25=35	35+40=75	75+20=95

Чтобы найти медианный интервал нужно объем выборки увеличенный на единицу разделить на 2 (т.е.(n+1)/2), а затем найти первый интервал, накопленная частота которого превышает либо равна полученному значению. В нашем случае (n+1)/2=48, а судя по ряду накопленных частот медианным является интервал 80-90%.

Находим:

 x₀ = 80;

 l =10;

n = 95;

s _μe–1 = 35;

f _μe =40.

,

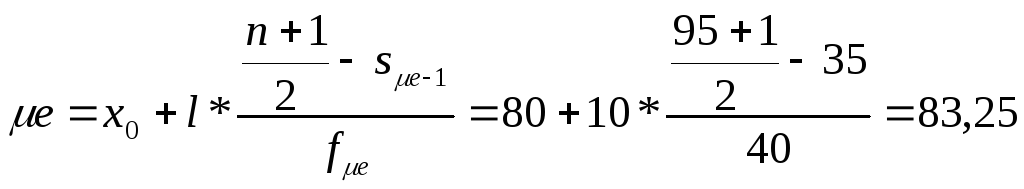Показатели (меры), характеризующие рассеяние относительно центральной тенденции. Средние позволяют охарактеризовать статистическую совокупность одним числом, однако, не содержат информации о том, насколько хорошо они представляют эту совокупность. Для определения того, насколько сильно варьируются значения признака, используются такие характеристики, как размах вариации, дисперсия и среднее квадратическое отклонение.

Все они показывают, насколько сильно варьируют значения признака (а точнее – их отклонения от среднего) в данной совокупности. Чем меньше значение меры разброса, тем ближе значения признака у всех объектов к своему среднему значению, а значит, и друг к другу. Если величина меры разброса равна нулю, значения признака у всех объектов одинаковы.

Размах вариации (R) – это разность между наибольшим и наименьшим значениями признака:

,

где x_max – максимальное значение признака;

      x_min – минимальное значение признака.

Показатель этот достаточно просто рассчитывается, однако является наиболее грубым из всех мер рассеяния, поскольку при его определении используются лишь крайние значения признака, а все другие просто не учитываются.

При расчете двух других характеристик меры вариации признака используются отклонения всех вариант от средней арифметической. Эти характеристики (дисперсия и среднее квадратическое отклонение) нашли самое широкое применение почти во всех разделах математической статистики.

Дисперсия (s ²) – абсолютная мера вариации (колеблемости) признака в статистическом ряду – средний квадрат отклонения всех значений признака ряда от средней арифметической этого ряда:

,

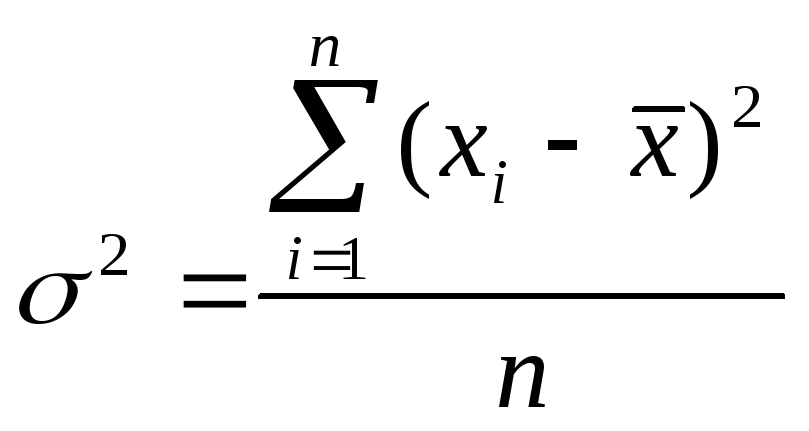где x_i – варианта с порядковым номером ;

     –средняя арифметическая;

     n – объем совокупности.

Дисперсия для вариационного ряда рассчитывается по формуле: 

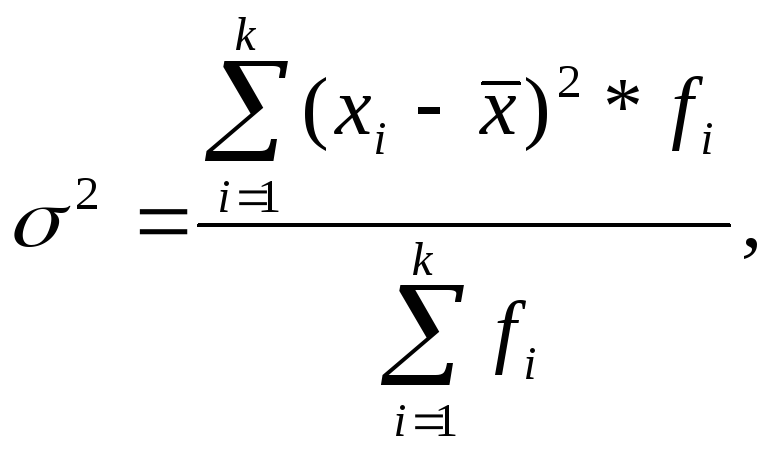
где – среднее значение признака;

x_i – индивидуальное значение признака;

f_i – общее число единиц наблюдения.

Следует отличать теоретическую (генеральную) дисперсию — меру измен­чивости бесконечного числа измерений (в генеральной совокупности, попу­ляции в целом) и эмпирическую, или выборочную, дисперсию — для реально измеренного множества значений признака. Выборочное значение в стати­стике используется для оценки дисперсии в генеральной совокупности. Выше указана формула для генеральной (теоретической) дисперсии, которая, понятно, не вычисляется. Для вычислений используется формула выбороч­ной (эмпирической) дисперсии, отличающаяся знаменателем:

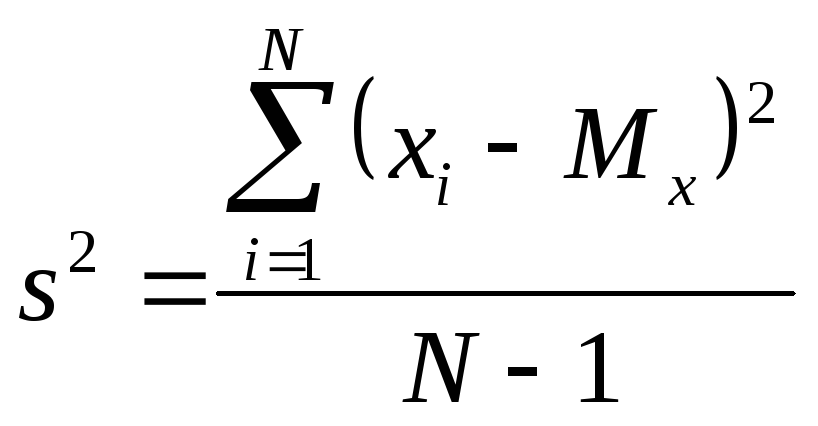
Для качественных шкал рассчитывается дисперсия доли. При наличии двух взаимоисключающих вариантов значений признака говорят о наличии альтернативной изменчивости качественного признака. Эквивалентом такого признака будет переменная, которая принимает значение 1, если обследуемая единица обладает данным признаком, и значение 0, если обследуемая единица не обладает им. К такому виду можно привести любую переменную, выделив группу единиц, обладающих данным значением признака, и группу единиц, обладающих всеми остальными значениями признака. Тогда дисперсия доли будет рассчитана по формуле:

,

где p – доля единиц, обладающих данным значением признака

Дисперсия применяется как для оценки рассеяния признака, так и для определения ошибки репрезентативности.

Дисперсия выражает разброс в «единицах в квадрате» (например, в «рублей в квадрате»). Для представления меры вариации в тех же единицах, что и варианты, используется среднее квадратическое (стандартное) отклонение, которое интерпретировать гораздо проще, т.к. выражается в привычных для нас единицах (например, в «рублях»).

Среднее квадратическое (стандартное) отклонение (s) – это квадратный корень из дисперсии и рассчитывается как:

или .

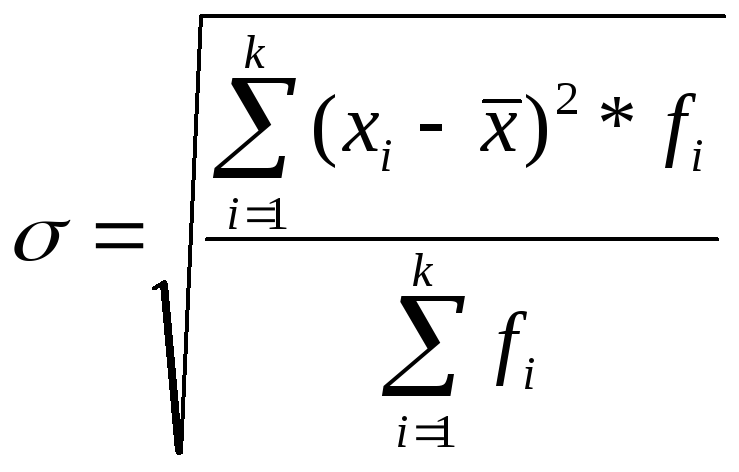Для выборки:

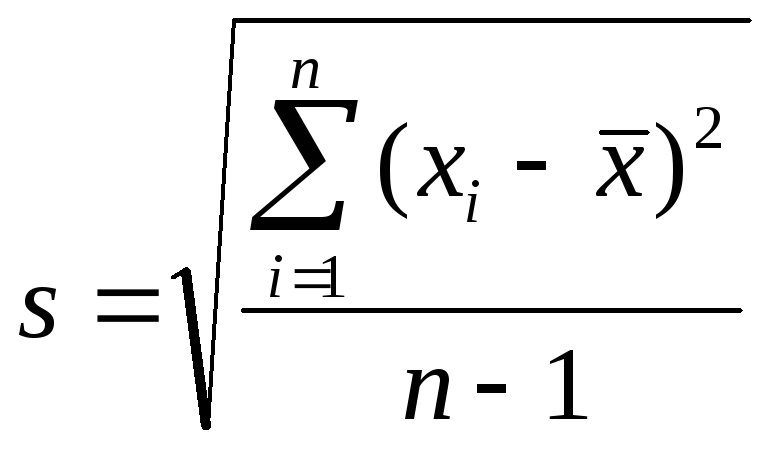или .

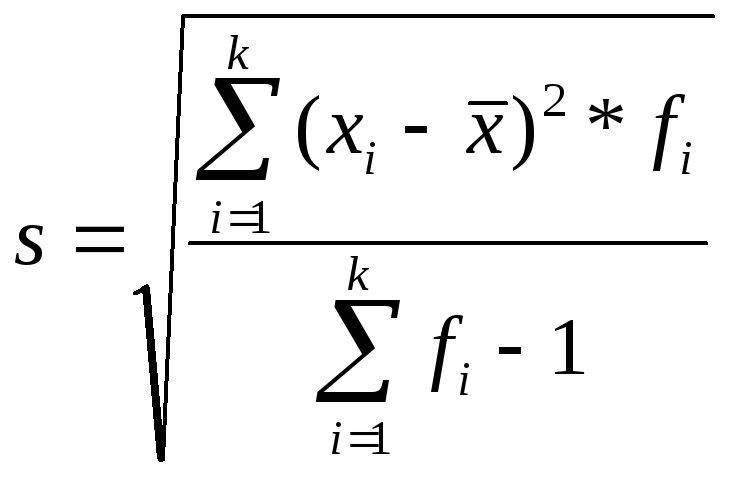Стандартное отклонение показывает, насколько в среднем индивидуальные значения признака отличаются от среднего.

В случае, когда набор данных имеет нормальное распределение, стандартное отклонение приобретает особый смысл. На рис. 3 по обе стороны от среднего сделаны отметки на расстоянии одного, двух и трех стандартных отклонений соответственно. Так, примерно 66,7% (две трети) всех значений находятся в пределах одного стандартного отклонения по обе стороны от среднего значения, 95% значений окажутся в пределах двух стандартных отклонений от среднего и почти все данные (99,7%) будут находиться в пределах трех стандартных отклонений от среднего значения. Это свойство стандартного отклонения для нормально распределенных данных называется «правилом двух третей».

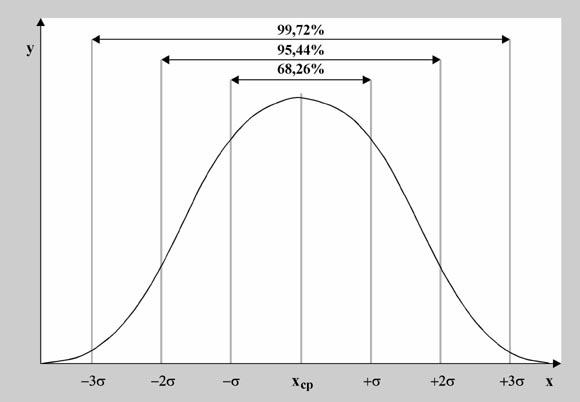
Рис. 3. Свойство стандартного отклонения для нормально распределенных данных

Рассмотренные меры рассеяния – абсолютные величины. Однако часто бывает необходимо сравнить вариацию одного и того же признака у разных групп объектов, выявить степень различия одного и того же признака у одной и той же группы объектов в разное время, сопоставить вариацию разных признаков у одних и тех же групп объектов. Для решения этих задач необходимо использовать относительные показатели. Таким показателем является коэффициент вариации.

Коэффициент вариации (V) – это отношение стандартного отклонения к средней арифметической, выраженное в процентах:

.

Совокупность считается однородной, если коэффициент вариации не превышает 35% (для распределений, близких к нормальному).

Коэффициент вариации часто используют при проведении сравнений выборок различных объемов.

Следует отметить, что при ассиметричном (скошенном) распределении данных коэффициент вариации может превысить 100%. Такой результат означает, что в изучаемой ситуации наблюдается очень сильный разброс данных относительно среднего.

Пример. Определим выборочные дисперсию, стандартное отклонение и коэффициент вариации для данных из предыдущего примера.

1. Рассчитаем дисперсию выборки:

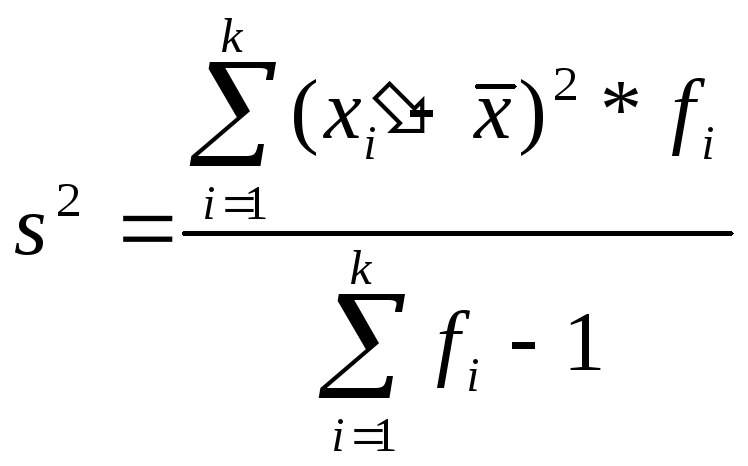, (см. расчетную табл. 9)

Таблица 9

Расчетная таблица

xi	fi	xi'
60-70	10	65	-17	289	2890
70-80	25	75	-7	49	1225
80-90	40	85	3	9	360
90-100	20	95	13	169	3380
Итого Σ	95				7855

2. Рассчитаем стандартное отклонение как =8,98

3. Рассчитаем коэффициент вариации

Показатели асимметрии. В рамках данной группы показателей выделим коэффициенты асимметрии и эксцесса.

Асимметрия – показатель, отражающий перекос распределения относительно среднего арифметического влево или вправо. В тех случаях, когда какие-нибудь причины благоприятствуют более частому появлению значений, которые выше или, наоборот, ниже среднего, образуются асимметричные распределения.

При положительной асимметрии в распределении чаще встречаются более низкие значения признака, а при отрицательной - более высокие.

Сильная асимметрия встречается в специфических выборках. Если мы возьмем учеников-отличников и измеряем IQ, то вероятно получим распределение, скошенное вправо (в сторону высоких баллов). Так же, изучая экстраверсию менеджеров, мы, скорее всего получим скошенное распределение в сторону сильной экстраверсии, т. к. большая часть менеджеров общительные люди.

Эксцесс – показатель, отражающий высоту распределения. В тех случаях, когда какие-либо причины способствуют преиму­щественному появлению средних или близких к средним значений, об­разуется распределение с положительным эксцессом. Если же в рас­пределении преобладают крайние значения, причем одновременно и более низкие, и более высокие, то такое распределение характеризуется отрицательным эксцессом и в центре распределения может образоваться впадина, превращающая его в двухвершинное.

Можно говорить о нормальности распределения, если асимметрия находится в интервале [–0.2;+0.2], а эксцесс – в интервале [2;4].

Выбор показателей зависит от исследовательских задач и от уровня, на котором замерен признак. Для шкал более высокого уровня можно использовать все показатели, которые используются для шкал более низкого уровня, но не все показатели, используемые для шкал более высокого уровня можно использовать для шкал более низкого уровня (табл. 10).

Таблица 10

Примеры использования статистических методов в зависимости от шкалы измерения

Шкала	Тип	Типичные примеры	Показатели закона распределения	Меры положения «центральной тенденции»	Меры рассеяния относительно центральной тенденции
Наименований (номинальная)	Качественные	Нумерация игроков футбольной команды	Частоты, проценты	Мода	Дисперсия доли
Порядковая (ординальная)		Ранжирование лиц по признаку (лучше – хуже)	Частоты, проценты	Мода, медиана	Дисперсия доли
Интервальная	Количественные	Температура по Цельсию или Фаренгейту, энергия, календарные даты	Частоты, проценты, накопленные частоты	Мода, медиана, средняя арифметическая	Размах вариации, стандартное отклонение, коэффициент вариации
Отношений		Длина, вес, сопротивление, шкала высоты звука, шкала громкости звука	Частоты, проценты, накопленные частоты	Мода, медиана, средняя арифметическая, средняя гармоническая, средняя геометрическая	Те же

Построение и анализ таблиц двухмерного распределения

Двухмерное распределение – это распределение единиц совокупности по двум переменным. Его анализ позволяет решать как описательные, так и аналитические задачи. Говоря об описательных задачах, мы имеем в виду, что мы можем охарактеризовать структуру совокупности по двум переменным. Аналитические задачи предполагают установление связи между переменными.

В статистике различают два вида статистической взаимосвязи: функциональную и корреляционную. Функциональной называется такая связь между двумя переменными, когда значение у однозначно определяется в зависимости от значений х. То есть каждому значению x соответствует свое значение y. Например, функционально связаны общий стаж работы y и стаж работы на данном предприятии x: y=ax+b, где b – стаж работы до поступления на предприятие, a зависит от особенностей работы. Обычно a=1, но в некоторых случаях (например, при работе на вредном производстве) один год засчитывается за большее количество времени, например, за два, тогда a=2.

В случае корреляционной связи значение y тоже определяется значением x, но не всегда. То есть, каждому значению x главным образом соответствует некоторое значение y, но не во всех случаях. Графически это можно изобразить следующим образом (рис.4)

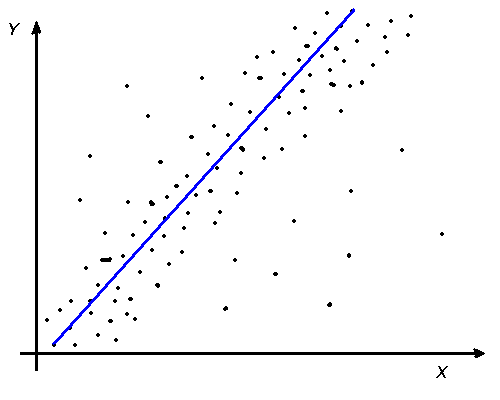
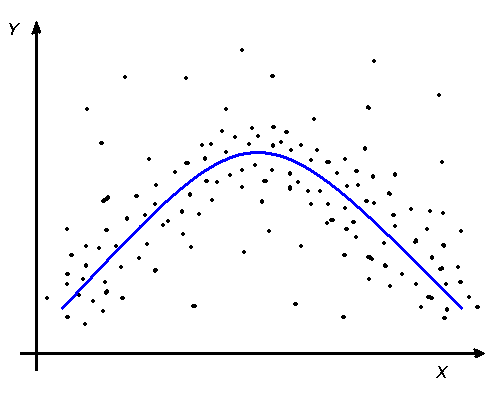
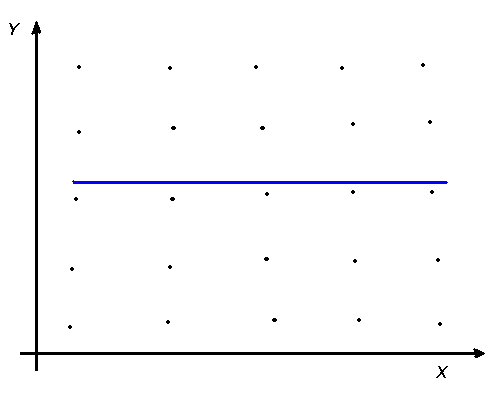
а) б) в)

Рис. 4. Пример графиков корреляционной взаимосвязи:

а) линейная прямая; б) нелинейная; в) нет связи

Это происходит в силу того, что на одну и туже переменную влияют несколько факторов. В такой ситуации для того, чтобы увидеть форму взаимосвязи надо рассчитать средний y для каждого x и рассматривать, как в среднем изменяется y при изменении y. Таким образом, функциональная взаимосвязь действует для всех случаев (каждому x или комбинации x₁, x₂,…,x_n соответствует одно значение y). Корреляционная взаимосвязь (каждому x или комбинации x₁, x₂,…,x_n соответствует несколько значений y) выступает только в средних цифрах. Например, если рассматривать зависимость производительности труда от стажа работников, мы увидим, что здесь наблюдается корреляционная зависимость, так как на производительность труда влияют также образование, здоровье, отношение к работе и другие факторы.

Нельзя отождествлять корреляционную и причинно-следственную связь. Наличие корреляции свидетельствует о том, что, либо одно явление является частичной причиной другого, либо оба явления – следствие общих причин. Для выводов о причинно-следственной связи необходимо использовать знание социологической теории.

Выделяют ряд характеристик взаимосвязи. Во-первых, это сила связи. Смысл этой характеристики зависит от того, какие коэффициенты корреляции мы используем.

Следующая характеристика – линейность связи. Она используется, когда переменные замерены не ниже, чем на порядковом уровне. Связь может быть прямолинейная, если линия, проведенная через средние значения y прямая, и криволинейная, если линия, проведенная через средние значения y кривая. Эти ситуации отращены соответственно на графиках а) и б).

Линейная связь имеет направление, то есть ее можно охарактеризовать как прямую или обратную. Прямая связь наблюдается, когда большему значению x соответствует большее значение y. Обратная – когда большему значению x соответствует меньшее значение y.

Помимо всего вышеназванного, при анализе взаимосвязи переменных необходимо оценить статистическую значимость связи. Связь считается значимой, если мы можем утверждать, что выявленная на выборочной совокупности закономерность проявляется и в генеральной. Для оценки значимости связи существует целый ряд критериев. Выбор критерия значимости зависит от уровня измерения переменной и коэффициентов взаимосвязи, которые используются.

Анализ двухмерного распределения подчиняется следующей логике.

1. Формулировка гипотезы.

2. Выбор зависимой и независимой переменой.

3. Построение таблицы.

4. Поиск различий по таблице.

5. Оценка статистической значимости различий.

6. Оценка силы и направления связи.

7. Вывод по гипотезе и интерпретация результатов.

Формулировка гипотезы

Мы формулируем гипотезу о взаимосвязи между двумя переменными. Данная гипотеза в статистике обозначается H₁ и называется «альтернативной гипотезой». Альтернативная гипотеза о взаимосвязи обычно предполагает и «нулевую гипотезу» H₀, о том, что взаимосвязи нет. В результате проверки гипотезы мы должны либо принять нулевую гипотезу и сделать вывод, что связи нет, либо принять альтернативную гипотезу и сделать вывод, что связь есть.

Выбор зависимой и независимой переменой

Формулируя гипотезу, мы предполагаем, что одно переменная – X – будет независимой, то есть определяющей. Вторая переменная – Y – будет зависимой, то есть определяемой. Напомним, что корреляционная зависимость не говорит о наличии причинно-следственной связи, поэтому названия «зависимая» и «независимая» переменные используются условно.

Построение таблицы

Построение корреляционной таблицы. Для анализа корреляционной связи двухмерное распределение представляется в виде таблицы.

Таблица 11

Общий вид корреляционной таблицы двух признаков

Y	X						Всего
	x1	x2	…	xj	…	xk
y1	f11	f12	…	f1j	…	f1k	n1
y2	f21	f22	…	f2j	…	f2k	n2
…	…	…	…	…	…	…	…
yi	fi1	fi2	…	fij	…	fik	ni
…	…	…	…	…	…	…	…
ym	fm1	fm2	…	fmj	…	fmk	nm
Итого	n1	n2	…	nj	…	nk	n

В этой таблице:

f_ij – обозначения внутриклеточных частот, показывают, сколь раз в совокупности встречаются совместно i-е значение Y и j-е значение X.

n_i – маргиналы (итоговые частоты) по Y, показывают, сколько раз в совокупности встречается i-е значение Y.

n_j – маргиналы (итоговые частоты) по X, показывают, сколько раз в совокупности встречается j-е значение X.

N – объем изучаемой совокупности.

Рассмотрев таблицу, мы видим, что каждому значению X соответствует не одно определенное значение Y, а распределение.

Построение таблицы средних. Если зависимая переменная является количественной и замерена с помощью метрической шкалы, для выявления связи между переменными мы можем построить таблицу средних. Для этого независимая переменная, представляется в виде категорий, и для каждой категории рассчитывается среднее по зависимой переменной.

Таблица 12

Общий вид таблицы средних

X	Объем групп		Стандартное отклонение	Коэффициент вариации	Предельная ошибка ±
x1	n1		σ1	υ1	±Δ1
x2	n2		σ2	υ2	±Δ2
…	…	…	…	…	…
xi	ni		σi	υi	±Δi
…	…	…	…	…	…
xk	nk		σk	υk	±Δk
В целом по массиву	n		σ0	υ0	±Δ0

В этой таблице:

–средние значения зависимой переменной Y для каждого значения независимой переменной X.

υ_i – коэффициент вариации зависимой переменной Y для каждого значения независимой переменной X.

±Δ_i – предельная ошибка средних значений зависимой переменной Y для каждого значения независимой переменной X.

n_i – объем групп по независимой переменной X.

Поиск различий по таблице

В нашей корреляционной таблице приведены абсолютные значения. Для того чтобы сделать предварительные выводы о наличии взаимосвязи признаков, необходимо рассчитать относительные, а именно проценты. В аналитических целях мы рассчитываем проценты по независимой (Y) переменой. Для этого за 100 процентов берем маргинальные частоты по X. Теперь мы можем сравнивать между собой группы, образующие независимую переменную, по такому показателю как доля единиц, обладающих определенным значением зависимой переменной. Если эти доли отличаются, мы можем предположить связь между переменными.

Используя таблицу средних, мы можем сравнить между собой группы, образующие независимую переменную, по такому показателю как среднее значение зависимой переменной. Если мы видим различия между этими показателями, то можем предположить связь между двумя переменными.

Оценка статистической значимости различий

Обнаруженные различия между долями и между средними проявляются на обследованной нами совокупности. В случае, когда исследование было сплошным, мы можем этим удовольствоваться. Но чаще всего исследование бывает выборочным, то есть для того, чтобы делать выводы, мы должны проверить, проявляются ли эти различия в генеральной совокупности, которая нас и интересует. Для этого существует ряд критериев.

Для оценки значимости различий между долями или средними используется t-критерий Стьюдента.

Сравнение долей осуществляется по формуле:

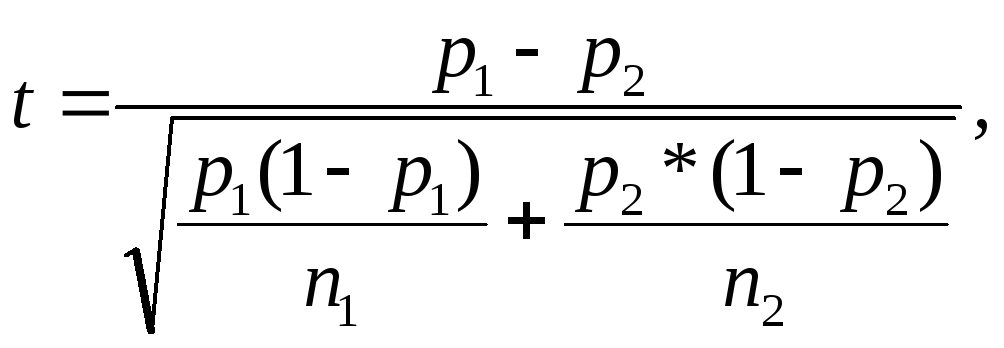
где p_1 – доля в первой группе,

p₂ – доля во второй группе,

n₁ – объем первой группы,

n₂ – объем второй группы

Сравнение средних осуществляется по формуле:

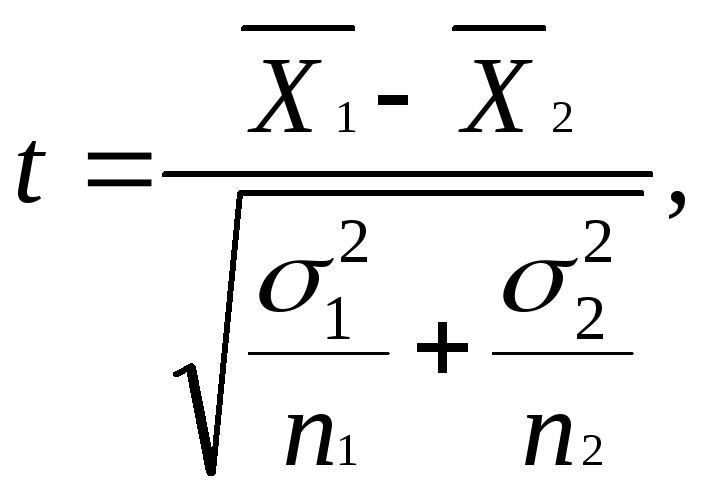
где – среднее для первой группы,

– дисперсия первой группы,

n₁ – объем первой группы (число чел.)

–среднее для второй группы,

– дисперсия второй группы,

n₂ – объем второй группы (число чел.)

Рассчитав значение t, мы должны его сравнить с критическими значениями из таблицы критических значений для t распределения (см. приложение) и определить вероятность ошибки. Если вероятность ошибки более 0,05, то обычно, такие различия считаются незначимыми, если же вероятность ошибки менее 0,05, то такие различия социологами признаются статистически значимыми.

Для оценки статистической значимости взаимосвязи в целом по таблице мы можем использовать критерий χ². С его помощью оценивают значимость отличий данного эмпирического распределения от теоретического распределением, специально рассчитанного таким образом, чтобы в таблице не было взаимосвязи между переменными. Рассчитывает χ² по формуле:

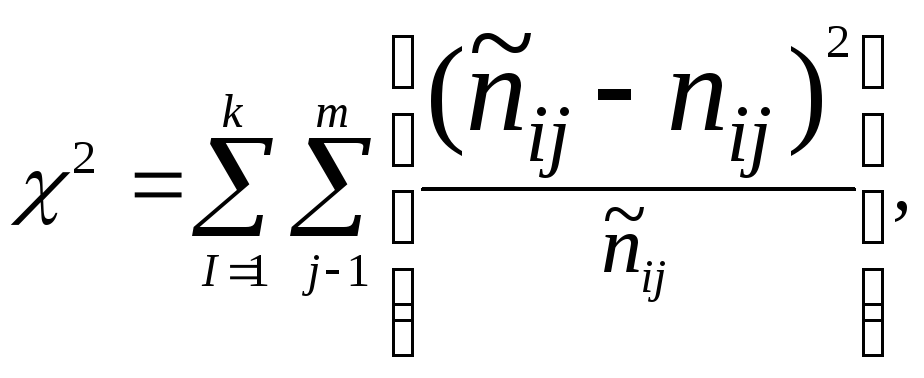
где – теоретические частоты, то есть те, которые были бы в ячейках таблицы

при абсолютной независимости признаков,

n_ij – эмпирические частоты,

k, m – число значений признаков

Рассчитав эмпирическое значение χ²_, мы должны сравнить его с табличным критическим значением. Для этого нам потребуется величина df (число степеней свободы):

df=(m–1)*(k–1),

где m – число строк в корреляционной таблице

k – число столбцов в корреляционной таблице

Теперь обращаемся к таблице критических значений. По строчке, соответствующей числу степеней свободы находим критическое значение χ² для вероятности ошибки не более 0,05. Если эмпирическое значение превышает критическое, принимаем альтернативную гипотезу. Если не превышает, тогда наши данные не позволяют отвергнуть нулевую гипотезу. Связь не значима. В этом случае можно действовать по следующей схеме (рис.5).

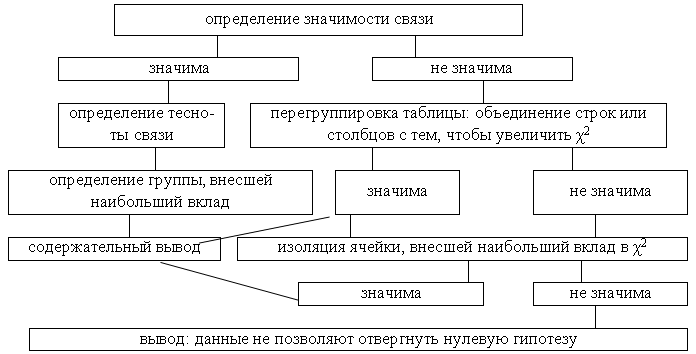
Рис.5. Схема оценки по χ²

Оценка силы и направления связи

Оценить силу связи можно при помощи величины коэффициента корреляции по модулю. Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0.

Направление связи оценивается с помощью знака коэффициента корреляции. Положительный коэффициент говорит о наличии прямой связи, а отрицательный – о наличии обратной связи.

Выбор коэффициента корреляции зависит от уровня, на котором замерены данные. Как мы помним, для шкал более высокого уровня можно использовать все показатели, которые используются для шкал более низкого уровня, но не наоборот. Для оценки связи между номинальными переменными, можно использовать только коэффициенты, основанные на совместном появлении событий.

Коэффициент Крамера, основан на использовании критерия χ²:

,

где n – общее число ответивших на оба вопроса,

m – число строк,

k – число столбцов,

min – надо выбрать наименьшее

Коэффициент Крамера измеряется от 0 до 1, причем, чем ближе коэффициент к 1, тем сильнее связь между двумя переменными. Коэффициент Крамера имеет смысл использовать только в том случае, если связь при помощи χ² признана значимой.

Если мы оцениваем связь двух дихотомических признаков, то мы можем использовать некоторые специфические меры связи. Для таких признаков строится корреляционная таблица размером 2*2, которая имеет следующий вид (табл.13)

Таблица 13

Корреляционная таблица

	B		Σ
A	a	b	a+b
	c	d	c+d
Σ	a+c	b+d	n

Для нее рассчитываются следующие коэффициенты:

Коэффициент ассоциации Юла		Коэффициент контингенции

Эти коэффициенты обладают следующими свойствами:

1. Изменяются в интервале (–1;+1), обращаются в 0 в случае отсутствия связи.

2. Q отражает полную связь (все А=В, но не все В=А), а Φ – абсолютную (все А=В, и все В=А).

3. Q обращается в 1(–1), если хотя бы в одной клетке таблицы частота равна 0, а Φ обращается в 1(–1), если 0 в двух клетках.

Для метрических и порядковых признаков могут использоваться меры, основанные на принципе ковариации, то есть на изучении совместных изменений в значениях признаков.

Коэффициент Пирсона можно использовать только для метрических шкал. Он имеет формулу:

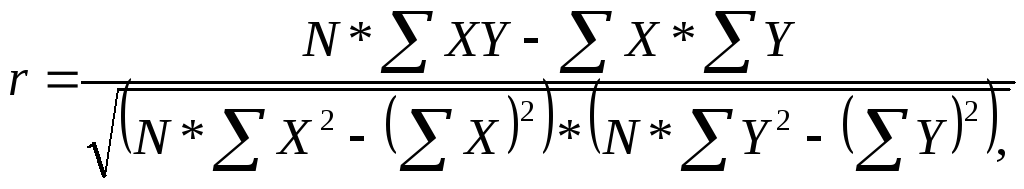
где X – значение независимой переменной,

Y – значение зависимой переменной,

N – объем совокупности.

Обе переменные X и Y должны быть в дискретном виде.

Значимость коэффициента можно оценить следующим образом.

Для случая, когда объем совокупности меньше 50, рассчитывается t-критерий по формуле

Для случая, когда объем совокупности больше 50, рассчитывается Z-критерий по формуле

В большинстве случаев востребованным и весьма полезным может оказаться построение и анализ диаграмм рассеяния. Диаграмма рассеяния (точечная диаграмма) – математическая диаграмма, изображающая значения двух переменных в виде точек надекартовой плоскости. На такой диаграмме производится визуальный анализ объектов исследования с учетом по форме связи («облака» точек) и по наличию выбросов на диаграмме рассеяния. «Выбросы» – крайние значения признаков, не характерные для данной выборки, слишком большие или слишком малые значении, аномальные, при удалении которых связь полностью может измениться.

Коэффициент ранговой корреляции Спирмена позволяет определить силу и направление связи между двумя признаками или двумя иерархиями признаков:

,

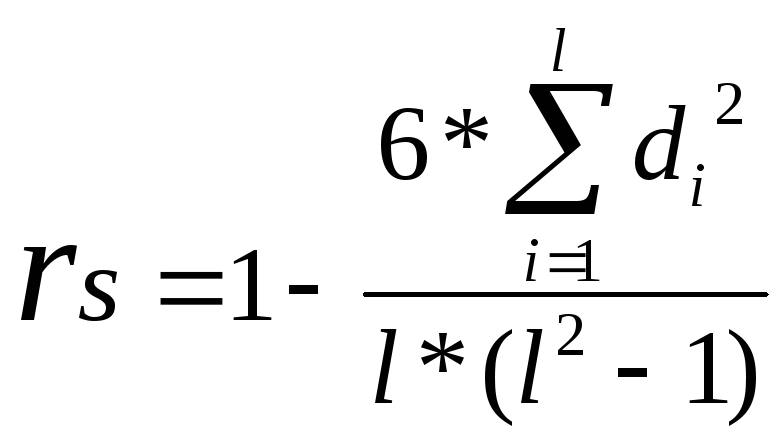где d_i – разница между парой рангов,

l – количество сравниваемых пар рангов

Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы.

В случае 1, когда сравниваются два признака, ранжируются индивидуальные значения по первому признаку, полученные испытуемыми, а затем индивидуальные значения по другому признаку. Если два признака связаны положительно, то испытуемые, имеющие низкие ранги по одному из них, будут иметь низкие ранги и по другому, а испытуемые, имеющие высокие ранги по одному из признаков, будут иметь по другому признаку также высокие ранги. Если же корреляция отсутствует, то все ранги будут перемешаны и между ними не будет никакого соответствия. В случае отрицательной корреляции низким рангам испытуемых по одному признаку будут соответствовать высокие ранги по другому и наоборот.

В случае 2, когда сравниваются две иерархии признаков, ранжируются значения, полученные в двух группах по определенному, одинаковому для двух групп набору признаков. Если эти иерархии связаны положительно, то признаки, имеющие низкие ранги в одной группе, будут иметь низкие ранги и в другой группе и наоборот. При отрицательной корреляции картина обратная: признаки, имеющие высокие ранги в одной группе, имеют низкие ранги в другой.

Значимость коэффициента Спирмена определяется при помощи таблицы критических значений (см. Приложение).

В социологических исследованиях часто объект удается охарактеризовать не по абсолютной, а по относительной интенсивности свойства. Таким образом, известна лишь последовательность, в которой располагаются объекты, то есть каждый объект описывается с помощью рангов по каждому признаку. Еще один коэффициент ранговой корреляции – коэффициент Кендалла – строится на основе отношений типа «больше – меньше» и имеет формулу:

;

где l – количество сравниваемых пар рангов

S – расчетная величина

S можно рассчитать следующим образом. Для расчета числа согласованных и несогласованных рангов упорядочивают ранжированные ряды по одному из признаков. После этого, рассматривая ранги для другого признака, подсчитывается для каждого ранга количество рангов, больше данного, находящихся в таблице ниже него. Это будут значения S⁺, то есть число согласованных рангов. После этого, подсчитывают для каждого ранга количество рангов, меньше данного, находящихся в таблице ниже него. Это будут значения S^–, то есть число несогласованных рангов. Затем из каждого количества согласованных рангов вычитают количество несогласованных рангов. Сумма этих величин и будет величина S.

Значимость коэффициента Кендалла определяется при помощи t-критерия Стьюдента, рассчитываемого по формуле:

,

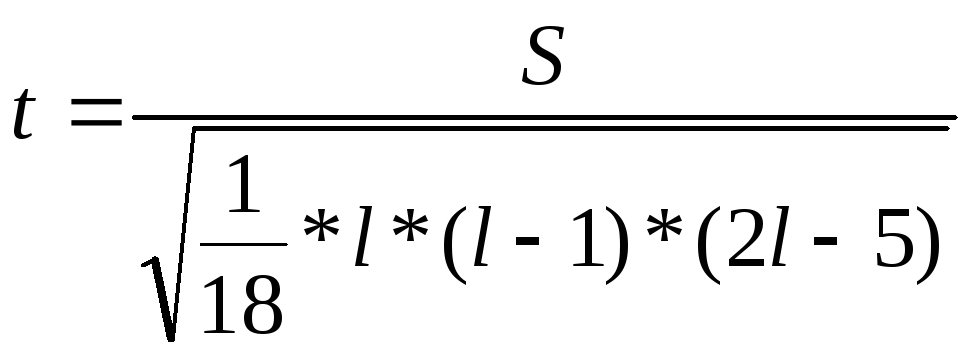где l – количество сравниваемых пар рангов;

S – расчетная величина.

Интерпретация коэффициента аналогична интерпретации коэффициента Спирмена.

Когда нам необходимо проанализировать изменение вариации значений одного признака под влиянием другого, имеет смысл использовать η-коэффициент (корреляционное отношение). Его использование основано на правиле сложения дисперсий.

Правило сложения дисперсий. Если рассчитать дисперсию признака по всей изучаемой совокупности, то она будет характеризовать вариацию как результат влияния всех факторов, определяющих индивидуальные различия в совокупности. Если же нужно выделить влияние какого-то одного фактора, то совокупность разбивают на группы, положив в основу группировки этот фактор. Выполнение такой группировки позволяет разбить общую дисперсию на две дисперсии, одна из которых будет характеризовать часть вариации, обусловленную влиянием интересующего нас фактора, а вторая – вариацию под воздействием всех прочих факторов.

Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия, которая является мерой колеблемости групповых средних вокруг общей средней:

,

где m – число групп

n_j – число единиц в j-ой группе;

–средняя арифметическая поj-ой группе;

–общая средняя арифметическая.

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия:

,

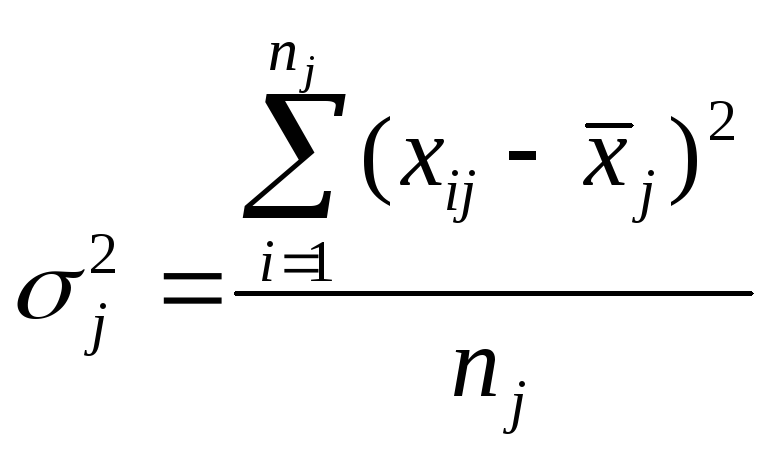где x_ij – индивидуальное значение признака;

–средняя арифметическая поj-ой группе;

n_j – количество единиц в совокупности.

По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий:

,

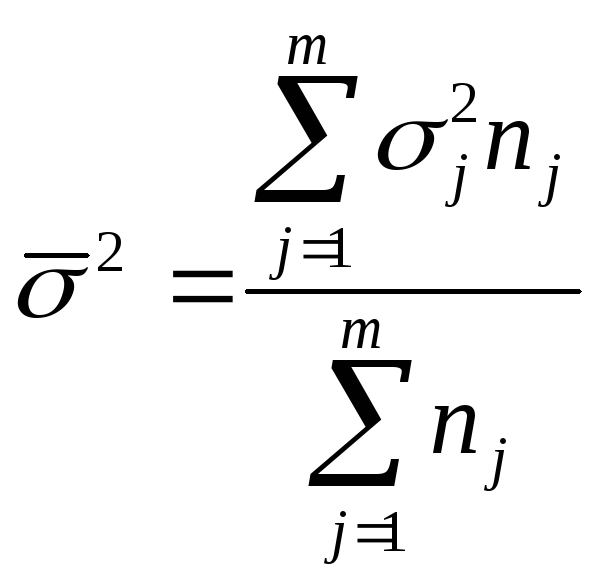где – внутригрупповая дисперсия;

n_j – количество единиц в совокупности.

Между общей дисперсией, внутригрупповой дисперсией и средней из внутригрупповых дисперсий существует соотношение, определяемой правилом сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

Для оценки влияния фактора нужно рассчитать долю межгрупповой дисперсии в общей – корреляционное отношение:

,

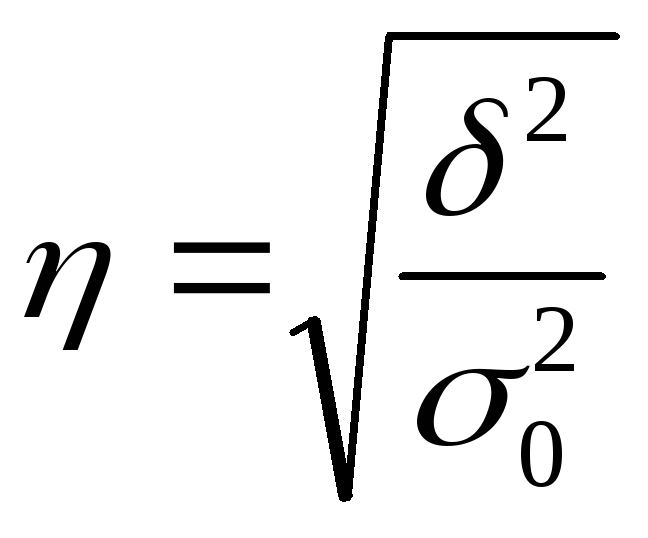где η_min=0, если δ²=0, тогда фактор не играет роли;

η_max=1, если δ²=σ²₀ (σ²_l=0), тогда вариация полностью обусловлена изучаемым фактором.

Проверить значимость η-коэффициента можно при помощи Z-критерия следующим образом:

, где N – объем совокупности.

Вывод по гипотезе и интерпретация результатов

Последний шаг – сделать вывод о гипотезе и провести интерпретацию результатов с точки зрения социологии. Наша гипотеза H₁ (о наличии взаимосвязи) может либо подтвердиться, либо быть опровергнутой (с определенной вероятностью ошибки) и тогда будет иметь смысл принять гипотезу H₀ (об отсутствии связи). Данный вывод мы сделаем на основании проверки статистической значимости различий. Так же (если это подразумевалось гипотезой) надо проверить соответствие гипотетической и эмпирической силы и направленности связи при помощи коэффициента корреляции.

Теперь надо вспомнить, что статистическая и социальная взаимосвязь – разные вещи. Статистическая взаимосвязь определяется по имеющимся данным, а социальная взаимосвязь носит объективный характер. Таким образом, нам надо объяснить вывод о проверке гипотезы с точки зрения социологических знаний, с точки зрения логики причинно-следственных отношений. При этом необходимо учитывать, что статистический вывод может так же объясняться недостаточностью или ненадежностью данных.