КМ-АХД-краткий конспект лекций

bn единицам. Общее количество производимого продукта равно суммарной потребности в нем:

Известна стоимость перевозки единицы однородного продукта из каждого пункта производства в каждый пункт назначения (потребления). Обозначим ее cij, т.е. имеются mxn чисел, которые могут быть сведены в матрицу стоимости перевозок:

Целью планирования в данной экономической ситуации является составление такого плана перевозок (т.е. указания, из какого пункта отправления в какой пункт потребления и в каком количестве надо везти однородный продукт), чтобы:

-из каждого пункта отправления было вывезено все имеющееся там количество продукта и все доставлено потребителю;

-отсутствовали бы встречные перевозки;

-суммарная стоимость всех перевозок была бы минимальной.

Обозначим количество продукта, перевозимое из i-го пункта производства (поставки) в j-1 пункт потребления через xij.

Тогда ограничения по производимому продукту будут выглядеть следующим образом:

x11 x12 ... x1 j ... x1n a1

x21 x22 ... x2 j ... x2n a2

...

xm1 xm2 ... xmj ... xmn am

А ограничения по пунктам потребления:

Запрещение встречных перевозок записывается формально, как условие неотрицательности переменных, составляющих план перевозок:

xij 0 для всех i и j.

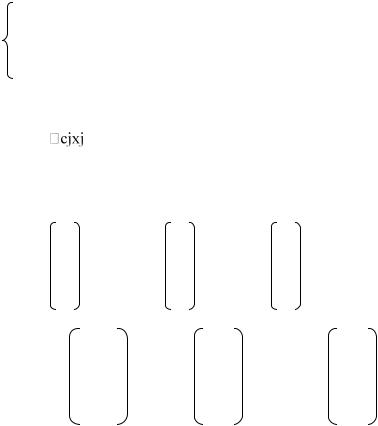
Целевая функция преследует минимизацию стоимости перевозок:

m n

cij xij min i 1 j 1

Это задача оптимизации перевозок, представляющая из себя задачу минимизации линейного программирования.

Нахождение решения задачи линейного программирования.

Решение любой задачи линейного программирования можно найти либо симплексным методом, либо методом искусственного базиса. Прежде чем применять один из указанных методов, следует записать исходную задачу в форме основной задачи линейного программирования, если она не имеет такой формы записи.

Симплексный метод.

Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного решения к другому, при котором значение целевой функции взрастает (при условии, что данная задача имеет оптимальное решение и каждое ее опорное решение является невырожденным). Указанный переход возможен, если известно какое-нибудь исходное опорное решение. Рассмотрим задачу, для которой это решение можно непосредственно записать.

Пусть требуется найти максимальное значение функции

F= c1x1 + c2x2+…+cnxn

При условиях

x1 + a1m+1xm+1 +…+a1nxn = b1 x2 + a2m+1xm+1 +…+a2nxn = b2

………

xm + amm+1xm+1 +…+amnxn = bm xj>=0 (j=1…n)

Здесь aij, bi ,cj (i=1..m, j=1..n) – заданные постоянные числа (m<n и bi>0)

При условиях

x1P1 + x2P2 +…+xmPm +…+xnPn = P0, xj>=0(j=1..n)

где

Так как b1P1 + b2P2 +…+bmPm =P0 то по определению опорного решения Х=(b1; b2;…;bm; 0;…;0) является опорным решением данной задачи (последние n-m компонент вектора Х раны нулу). Это решение определяется системой единичных векторов Р1, Р2, …, Рm, которые образуют базис m-мерного пространства. Поэтому каждый из векторов Р1, Р2,…,Pn а также вектор Р0 могут быть представлены в виде линейной комбинации векторов данного базиса.

Пусть Pj= xijPi (j=0..n) i=1-m

Положим zj = (j=1..n); j =zj-cj (j=1..n). Так как векторы Р1, Р2,…,Pm – единичные, то xij = aij и zj= ciaij, а j = ciaij – cj (i=1..m)

Теорема 1.5 (признак оптимальности опорного решения). Опорное решение Х*= (х*1, х*2,…, x*m, 0,0,…,0) задачи (22)-(24) является оптимальным, если j >=0 для любого j (j=1..n)

Теорема 1.6 Если k<0 для некоторого j=k и среди чисел aik (i=1..m), нет положительных (aik<=0), то целевая функция (22) задачи (22)-(24) не ограничена на множестве ее решений.

Теорема 1.7 Если опорное решение Х задачи (22)-(24) не вырожден и k <0 , но среди чисел aik есть положительные (не все aik<=0), то существует опорное решение Х’ такое, что F(X’)> F(X).

Сформулированные теоремы позволяют проверить, является ли найденное опорное решение оптимальным, и выявить целесообразность перехода к новому опорному решению.

Исследование опорного решения на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного решения, записать так, как показано в таблице.

Встолбце Сб этой таблицы записывают коэффиценты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.

Встолбце Ро записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов Pi представляют собой коэффиценты разложения этих векторов по векторам данного базиса.

Втаблице первые m строк определяются исходными данными задачи, а показатели (m+1)-й строки вычисляют. В этой строке в столбце вектора Ро записывают значение целевой функции, которое она принимает при данном опорном плане, а в

столбце вектора Pj – значение j = zj-cj.

Значение zj находится как скалярное произведение вектора Pj(j=1..m) на вектор Сб =(c1, c2,…,cm)

Zj = ci*aij (j=1..n)

Значение Fо равно скалярному произведению вектора Ро на вектор Сб:

Fо= cibi

После заполнения таблицы исходный опорный план проверяют на оптимальность. Для этого просматривают элементы (m+1)-й строки таблицы. В результате может иметь место один из следующих трех случаев:

1)j >=0 для j=m+1, m+2…,n (при j=1..m, zj= cj). Поэтому в данном случае числа j>=0 для всех j от 1 до n.

2)j<0 для некоторого j, и все соответствующие этому индексу величины aij<=0 (i=1..m)

3)j<0 для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел aij положительно.

Впервом случае на основании признака оптимальности исходный опорный план является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве планов, а в третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. Этот переход от

А коэффициенты разложения векторов Pj через векторы нового базиса, соответствующего новому опорному плану, - по формулам:

Aij- (arj/ark) при i r

A’ij = arj/ark при i=r

После вычисления b’i и a’ij согласно формулам (25) и (26) их значения заносят в таблицу 1.4. Элементы (m+1)-й строки этой таблицы могут быть вычислены либо по формулам

F’o = Fo –(br/ark) k’j = j – (arj/ark) k

либо на основании их определения.

Наличие двух способов нахождения элементов (m+1)-й строки позволяет осуществлять контроль правильности проводимых вычислений.

Из формулы (27) следует, что при переходе от одного опорного плана к другому наиболее целесообразно ввести в базис вектор Pj имеющий индекс j, при котором максимальным по абсолютной величине является число (br/arj) j ( j<0, arj>0). Однако с целью упрощения вычислительного процесса в дальнейшем будем вектор, вводимый в

базис, определять, исходя из максимальной абсолютной величины отрицательных чиселj. Если таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел cj, определяемых данными числами j ( j<0)

Итак, переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой. Элементы новой симплекс-таблицы можно вычислить как с помощью рекурентных формул (25)-(28), так и по правилам, непосредственно вытекающим из них. Эти правила состоят в следующем.

В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.

Элементы векторов Ро и Pj в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы

делением их на величину разрешающего элемента. В столбце Сб в строке вводимого вектора проставляют величину ck где л – индекс вводимого вектора.

Остальные элементы столбцов вектора Ро и Pj новой симплексной таблицы вычисляют по правилу треугольника. Для вычисления какого-нибудь из этих элементов находят три числа:

1)число, стоящее в исходной сиплекс-таблице на месте искомого элемента новой симплекс-таблицы

2)число, стоящее в исходной симплекс-таблице на пересечении строки,

вкоторой находится искомый элемент новой симплексной таблицы, и столбца, соответствующего вектору, вводимому в базис.

3)Число, стоящее в новой симплексной таблице на пересечении столбца, в котором стоит исходный элемент, и строки вновь вводимого в базис вектора (как отмечено выше, эта строка получается из строки исходной симплекс-таблицы делением ее элементов на разрешающий элемент)

Эти три числа образуют своеобразный треугольник, две вершины которого

соответствуют числам, находящимся в исходной симплекс-таблице, а третьячислу, находящемуся в новой симплекс-таблице. Для определения искомого элемента новой симплекс-таблицы из первого числа вычитают произведение второго и третьего.

После заполнения новой симплекс-таблицы просматривают элементы (m+1)-й строки если все z’j-cj>=0, то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность, находят новый опорный план. Этот процесс продолжают до тех пор, пока либо не получат оптимальный план решения задачи, либо не устанавливают ее неразрешимость.

Анализ модели на чувствительность

Многие параметры задачи, а именно правые части ограничений – коэффициенты целевой функции могут изменяться. Поэтому после получения оптимального решения она подвергается анализу на устойчивость: по отношению к правым частям ограничений задачи; к коэффициентам целевой функции; к технико-экономическим коэффициентам.

Устойчивое решение при изменении внешних условий, соответственно а, в, с, сохраняет ограничения образующие точку решения.

По отношению к правым частям точка решения задачи делит все ресурсы на дефицитные и недефицитные.

Дефицитные – их изменение приводит к изменению точки решения. Изменение не дефицитных ресурсов не влияет на точку решения задачи.

При изменении ресурсов статус ресурса (дефицитный, недефицитный) может поменяться, что может существенно повлиять на решение задачи.

Изменение дефицитного ресурса, то есть его увеличение или уменьшение связано с перемещением его вдоль одного из недефицитных ресурсов до точки пересечения другого дефицитного ресурса с данным недефицитным. Эта точка (обозначим ее – точка К) указывает на предельное положение первого дефицитного ресурса при его увеличении. Когда первый дефицитный ресурс пройдет через точку К, он станет недефицитным, область допустимых значений будет определяться на графике другим многоугольником и точка решения задачи перейдет в точку К, причем с увеличением дефицитного ресурса значение целевой функции тоже увеличиться, и наоборот.

Для определения пределов увеличения необходимо найти:

1.координаты точки К, для этого решим совместно два ограничения пересечением которых образована эта точка: К(X;Y)

2.новое значение дефицитного ресурса в точке К: b’=x1+2x2 (например)

3.значение целевой функции в точке К: Z

4.академиком Кандаровичем введено понятие объективно обусловленных оценок. двойственная оценка – отношение приращения целевой функции к приращению дефицитного ресурса. Экономический смысл: показывает, насколько увеличивается целевая функция при увеличении дефицитного ресурса на одну единицу.

обозначается - y1: y1= Zk-Zmax b’- b

пределы уменьшения ресурса определяют по такой же схеме:

1.координаты точки нижнего предела.

2.новое значение дефицитного ресурса: b”

3.новое значение целевой функции: Z

4.двойственная оценка: y1’

Решение задачи будет устойчивым пока двойственные оценки в обоих случаях будут равны: y1=y1’. Это условие будет выполняться пока правая часть ограничений остается в пределах от b’ до b”.

Так же определяются пределы всех остальных дефицитных ресурсов.

Анализ оптимальных решений по отношению к целевым функциям.

F= 6x1 + 5x2 min

4x1 + 3x2 60

2x1 + x2 24

x1 +2x2 20

x1 18

x2 25

Решение:

1.4x1 + 3x2 = 60 a) x1=0 x2=20

x2=0 x1=15

б)(0;0) – входит в область допустимых значений.

2. 2x1 + x2 = 24

а) x1=0 x2=24 x2=0 x1=12

б) (0;0) – не входит в область допустимых значений.

3.x1 + 2x2 =20

а) x1=0 x2=10 x2=0 x1=20

б) (0;0) – не входит в область допустимых значений.

4.x1=18 (0;0)- входит в область допустимых значений.

5.x2= 25 (0;0)- входит в область допустимых значений. Точка решения задачи – точка А.

2.Дефицитными в данной задача являются 2 и 3 ресурсы, остальные дефицитными не являются. Определим координаты точки А.

Для этого совместно решим уравнения описывающие линии ограничений в результате пересечения которых получена данная точка решения.

2x1+ x2 = 24

x1 + 2x2 = 20

то есть координаты точки А(28/3; 16/3)

Значение целевой функции Z в данной точке равно 6*(28/3)+5*(16/3)= 248/3

При изменении коэффициентов целевой функции происходит ее поворот относительно наклонной линии. Так как изменение коэффициентов целевой функции приводит к повороту целевой функции относительно точки оптимального решения, возникает проблема сохранения устойчивости решения.

До совпадения целевой функции с любым из дефицитных ресурсов – решение устойчиво. Дальнейшее изменение коэффициентов приводит к перемещению точки решения задачи в точку В или в точку С.

6x1+5x2 = Z для того, чтобы график функции поворачивался, коэффициент 6 2x1+x2 = 24 должен измениться.

С1x1+ 5x2 =Z разделим первое уравнение на 5

2x1 + x2 = 24

С1/5*x1+ x2 = Z/5 Поскольку результатом поворота графика является 2x1 + x2 = 24 совпадение графика целевой функции Z с графиком

ограничения, то очевидно, что C1/5 = 2 и Z/5=24,т.е. С1=10 и Z=120. Значит, увеличение С1 для данной задачи возможно до значения 10, при этом устойчивость решения задачи сохраняется, а значение целевой функции Z увеличивается, что приводит к ухудшению оптимального решения.

Выполняем аналогичные действия по отношению ко второму дефицитному ресурсу.

C1x1+ 5x2 =Z Разделим первое уравнение на 5, а второе на 2

X1 + 2x2 = 20

С1/5*x1 + x2 = Z/5 Очевидно, что С1/5= ½, а Z/5 = 10 X1/2 + x2 = 10

То есть, С1= 5/2, а Z=50.

В итоге получаем, что коэффициент С1 для данной задачи может меняться в интервале от 2,5 до 10 (2,5 - 10) и при это целевая функция меняется в пределах от 50 до 120.

Далее выполняются аналогичные действия по отношению к коэффициенту С2, целевой

В итоге получаем, что до совпадения графика целевой функции с графиком второго дефицитного ограничения С2 меняется в пределах от 3 до 12, при этом целевая функция Z меняется в пределах от 72 до 120.

При большом количестве переменных, решение без использования компьютеров невозможно.

Тогда задаются новыми значениями коэффициентов целевой функции, и определяются граничные значения, при которых меняются координаты точки решения и двойственная оценка.

Рекомендуемая литература

7.Калашников В.В. Организация моделирования сложных систем. - М.: Высшая школа, 1990.

8.Кобелев Н.Б. Практика применения экономико-математических методов и моделей/ Учеб.-практ.пособие. – М.: ЗАО «Финстатистинформ», 2000.- 246 с., с.3132).

9.Лукасевич И.Я. Анализ финансовых операций. Методы, модели, техника вычислений. – М.: Финансы, ИНИТИ, 1998

10.Ричард Томас. Количественные методы анализа хозяйственной деятельности/Пер. с англ. –М.: Издательство «Дело и Сервис», 1999.

11.Советов Б.Я., Яковлев С.А. Моделирование систем. - М.: Высшая школа, 1998.

12.Таха Х. Введение в исследование операций: В 2-х книгах. Пер. с англ. – М.: Мир,

1985.

Модели управления запасами

1.Литература

2.Обобщенная модель управления запасами

3.Модель оптимального размера заказа, точка заказа, модель с разрывом цен

4.Модель размера производственного заказа

5.Модель периодической проверки

6.Модели управления запасами при неопределенном спросе

7.Многопродуктовая модель управления запасами

8.Практические вопросы при управлении запасами

9.Решение типовой задачи

1. Литература

Использованная при подготовке курса:

1.Ричард Томас. Количественные методы анализа хозяйственной деятельности/Пер. с

англ. – М.: Издательство «Дело и Сервис»,1999. – 432 с.

2.Таха Хамди. Введение в исследование операций. М.: Мир, 1985

Рекомендуется для самостоятельного обучения:

1.Исследование операций в экономике: Учебн. пособие для вузов/ Н.Ш.Кремер, Б.А.

Путко и др.; Под ред. проф. Н.Ш.Кремера. – М.: ЮНИТИ, 2000. – 407 с.

2.Обобщенная модель управления запасами

Управление запасами – важная сфера управленческой деятельности на многих предприятиях различных отраслей как по производству товаров, так и по оказанию услуг.

В условиях рыночной экономики становятся особенно актуальными вопросы рациональной и эффективной организации процессов управления и контроля за движением материальных и финансовых потоков на предприятии с целью повышения эффективности материально-технического снабжения самого предприятия и сбыта производимой им готовой продукции. Это необходимо для оптимизации уровня запасов и эффективного их использования, уменьшения их уровня, а также минимизации оборотных средств, вложенных в эти запасы.

Недостаток производственных запасов у предприятия приводит к нарушению ритмичности его производства, снижению производительности труда, перерасходу материальных ресурсов из-за вынужденных нерациональных замен и повышению