3.3 Неопределенный интеграл

Функия называется первообразной для функции на промежутке Х, если в каждой точке х этого промежутка справедливо равенство.

Совокупность всех первообразных для функции на промежутке Х называется неопределенным интегралом от функциии обозначается, где С – произвольная постоянная. В записифункцияназывается подинтегральной функцией, а- подинтегральным выражением. Нахождение неопределенного интеграла от некоторой функции называется интегрированием этой функции. Операции интегрирования и дифференцирования взаимно обратны.

Основные свойства неопределенного интеграла

1.

2.

3.

4. , где- некоторое число

5.

Табличные интегралы

1.

2. , где

3.

4. , где

5.

6.

7.

8. , где

9.

10.

11.

12.

13.

Методы интегрирования

Основное содержание различных методов нахождения интегралов состоит в сведении искомого интеграла к табличному или сумме интегралов. В простейших случаях это удается сделать, используя лишь эквивалентные преобразования подынтегральной функции и, если необходимо, свойства интегралов.

1. Метод замены переменной

Пусть - функция, непрерывно дифференцируемая на рассматриваемом промежутке. Тогда

.

Эта формула называется формулой замены переменной в неопределенном интеграле.

Пример 1. Найти интеграл .

Решение. Сделаем замену , тогда, следовательно.

Тогда .

2. Метод интегрирования по частям

Пусть и- непрерывно дифференцируемые функции. Тогда справедлива формула:

.

Эта формула называется формулой интегрирования по частям.

Пример 2. Найти интеграл .

Решение. Пусть ,. Тогда,

Применяя формулу интегрирования по частям, получаем

.

Для нахождения последнего интеграла вновь применим формулу интегрирования по частям, сделаем замену ,. Тогда,.

Тогда .

Следовательно, искомый интеграл равен

.

3. Интегрирование рациональных выражений

Рассмотрим способы нахождения интегралов вида , гдеи- некоторые многочлены от переменной х.

Пусть знаменатель допускает разложение на линейные множители:

,

где прии- положительные целые числа. В этом случае дробьдопускает представление в виде суммы простейших дробей:

,

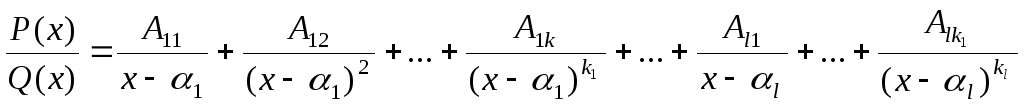где - некоторые неизвестные числа. Поэтому рассматриваемый метод интегрирования называется методом неопределенных коэффициентов.

В случае, когда многочлен не допускает разложения на линейные множители, в выражении дополнительно содержатся сомножители вида, тогда разложение дробидополнительно содержит слагаемые вида

Пример 3. Найти интеграл .

Решение. Разложим подинтегралную функцию на простейшие дроби:

.

Таким образом, , т.е.,

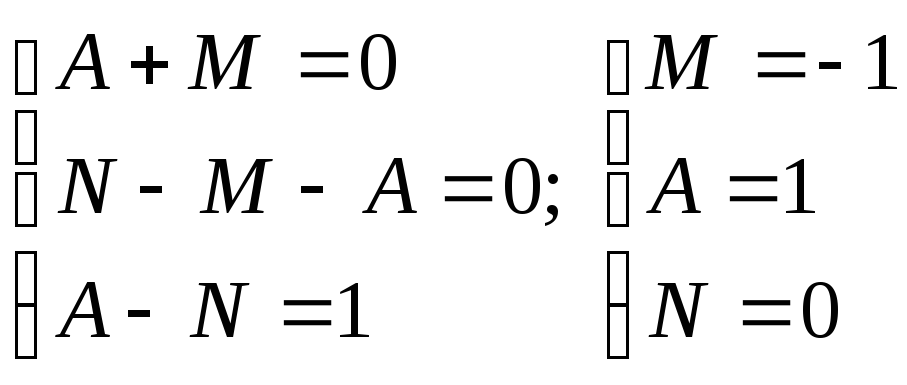
Разложение подынтегральной функции имеет вид:

.

.

Для первого интеграла преобразуем функцию под знаком дифференцила: , для второго – выделим полный квадрат в знаменателеи воспользуемся заменой переменной, тогда.

Тогда,

.

3.4 Определенный интеграл

Пусть функция задана на отрезке. Разобьем отрезокнаэлементарных отрезков точками.

В каждом из отрезков разбиения выберем произвольно точкуи положим. Тогда сумма вида

называется интегральной суммой для функции на отрезке.

Пусть существует и конечен предел S интегральной суммы при стремлении к нулю длины максимального элементарного отрезка , не зависящий от способа разбиения отрезкана части и способа выбора точекна отрезках разбиения. Тогда функцияназывается интегрируемой на, а числоS – определенным интегралом от наи обозначается.

Свойства определенного интеграла

1)

2)

3)

4)

5)

6) , если функциячетная

, если функция нечетная

7) Формула Ньютона-Лейбница

Геометрические приложения определенного интеграла

1. Если функция неотрицательна на отрезке, то площадьS под кривой на(площадь криволинейной трапеции, ограниченной кривойи прямыми) численно равна определенному интегралу отна данном отрезке:

(геометрический смысл определенного интеграла)

2. Если функция неположительна на отрезке, то площадьS над кривой начисленно равна определенному интегралу отна данном отрезке, взятому со знаком «минус»:

3. Если на отрезке, то площадьS фигуры, заключенной между кривыми ина этом отрезке определяется формулой

.