Дифференцирование функций, заданных параметрически

Если зависимость функциии аргументазадана посредством параметра:, то, или. (2)

Пример 1. Найти , если,. Это параметрические уравнения окружностис центром в начале координат и радиуса.

Решение. Находим и.

Отсюда .

Пример 2. Найти от функции:,.

Решение: ,,теперь по формуле (2)

найдем .

Производная неявной функции

Пусть уравнение не разрешено относительно функции, т.е. функциязадана неявно. Чтобы найти производную, надо продифференцировать левую и правую часть уравнения, учитывая, чтоесть функция аргумента. Рассмотрим это правило на примерах.

Пример 1. Найти , если а), б).

Решение: а) , выразив, получим.;

б) дифференцируя обе части этого уравнения, получим уравнение относительно :,;найдем теперь.

Геометрический смысл производной

Здесь – угол наклона касательной к графику функциии точке. Через две точкиикривойпроведем секущую, ее угловой коэффициент. Двигая точкупо кривой к точке, мы будем поворачивать секущую вокруг точки, в результате секущая стремится занять положение касательной, проведенной к графику в точке, а уголстремится к углу– наклона касательной, т.е.,

где – угловой коэффициент касательной. Известное уравнение прямойиспользуем как уравнение касательной, проведенной к графику функциив точке, с угловым коэффициентом. Тогда уравнение касательной примет вид

(3)

Задача. Найти уравнение касательной к графику функции а) 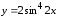в точке, б),в точке.

Решение. а) Сначала вычислим ординату точки касания . Затем производную в точке,

. Это угловой коэффициент касательной.

Подставим найденные параметры в уравнение (3)

–искомая касательная;

б) кривая задана параметрически; найдем координаты точки касания, подставив значение параметра в уравнение кривой: ,. Для отыскания углового коэффициентавоспользуемся формулой,, теперь запишем уравнение касательной , или.

Дифференциал функции и формула приближенного вычисления

Определение. Дифференциалом функции называется величина, пропорциональная бесконечно малому приращению аргумента, отличающаяся от соответственного приращения функциина величину более высокого порядка.

По определению производной: , откуда следует, что, где– бесконечно малая при, т. е. , тогда, где первое слагаемое и есть дифференциал

, ,. (4)

Определение дифференциала позволяет использовать его в приближенных вычислениях, заменив вычисление функции ее дифференциалом. Рассмотрим приращение функции: , или, тогда

. (5)

Это и есть формула приближенного вычисления. Ошибка, получаемая при приближенных вычислениях, есть бесконечно малая высшего порядка, чем приращение аргумента, т. к.

.

Задача 1. Найти дифференциалы функций:

а) , б), в).

Решение: а) , найдем сначалаи затем;

б) ,;

в) ,.

Задача 2. Найти приращение и дифференциал функции прии. Вычислить абсолютную и относительную ошибки, которые получаются при замене приращения функции ее дифференциалом.

Решение ,

;

Абсолютная ошибка , относительная ошибка

.

Задача 3. Вычислить приближенно а) , б).

Решение. Чтобы воспользоваться формулой (5) надо составить функцию (по виду вычисляемого выражения) и выбрать начальные условия так, чтобыбыло мало, аможно было легко подсчитать. В случае а) выбираем,,

, .

, ,

;

б) чтобы было мало, необходимо извлечь целую часть корня, т. е.

, откуда ,,,

, ,,теперь вычислим приближенно:

.

Производные и дифференциалы высших порядков

Определение 1. Производной второго порядка от функции называется производная от производной первого порядка и обозначается символомили, или.

Пример. ,,.

Определение 2. Производной -го порядка называется производная первого порядка от производной-го порядка и обозначаетсяили, или.

Пример. . Найти.

, ,!,

!, используя метод математической индукции, запишем формулу производной-го порядка!

Определение 3. Дифференциалом высшего порядка функции называется дифференциал от дифференциала -го порядка:

, в частности , здесь.

Пример: . Найти.

, ;

Тогда .

Производная второго порядка от функции, заданной параметрически.

Если , то производные,, последовательно могут быть вычислены по формулам:

=,,и т. д.

Для производной второго порядка имеет место формула .

Пример. Найти от функции

Решение. Найдем сначала ,,

тогда ,.

Правило Лопиталя. Раскрытие неопределенностей при вычислении пределов

Теорема. Предел отношения двух бесконечно малых или двух бесконечно больших существует и равен пределу отношения их производных:

, если выполняются условия:

1. функции идифференцируемы в некоторой окрестности точкиив этой окрестности.

2. 

(или ).

3. существует конечный или бесконечный.

Здесь может быть числом или одним из символов:.

Задача 1. Вычислить пределы: а) , б).

Решение. а) Подставив предельное значение аргумента , получаем неопределенность, т.к.,и функции дифференцируемы.

Найдем .

б) При имеем неопределенность. Применим правило Лопиталя:. Полученный предел снова представляет неопределенность вида, применяя еще раз правило Лопиталя, найдем.

Другие виды неопределенностей ,,можно свести к видуили.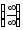

Задача 2. Найти предел .

Решение. Подставим предельное значение аргумента, получим неопределенность , которая легко сводится к частному:

=

=.

Возрастание, убывание функции. Точки экстремума

Определение 1. Функция называется возрастающей (убывающей) на некотором промежутке, если для любыхэтого промежутка().

Функция возрастающая (убывающая) называется монотонной.

Теорема 1. (Условие монотонности)

Если функция 1) определена на, 2) имеет конечную производнуюна, тогда, чтобыбыла возрастающей (убывающей) на, необходимо и достаточно, чтобы().

Задача 1. Найти интервалы монотонности функции .

Решение. Область определения функции дифференцируема всюду в области определения:.

Решим неравенство ,,

-это интервал возрастания функции.

Соответственно неравенство справедливо для всех– область убывания функции.

Определение 2. Точка называется точкой локального максимума (минимума), если в некоторой ее окрестностивыполняется неравенство() для всехэтой окрестности.

Теорема 2. (Необходимое условие существования экстремума)

Если 1) определена в окрестности точки, 2) дифференцируема в точкеи 3) имеет в ней локальный экстремум, то.

Точки, в которых производная называются критическими.

Замечание. Функция может иметь экстремум и в точках, где первая производная не существует. Например: Функция непрерывна в точке, но не дифференцируема т. к. односторонние пределы не равны, значит,не существует в точке, но функция имеет минимум.

Теорема 3. (Достаточное условие экстремума)

Если функция : 1) непрерывна в точке, 2) дифференцируема в некоторой области, 3)либо не существует и 4) при переходе через точкупроизводная меняет знак, то– точка экстремума, причем, если производная слева от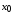отрицательна, а справа положительна, то– точка минимума; если слева отпроизводная положительна (функция возрастает) а справа отрицательна (функция убывает), то– точка максимума.

Замечание: в промежутке между критическими точками производная сохраняет знак, следовательно, это промежутки монотонности.

Теорема 4. (Исследование на экстремум с помощью второй производной или второе достаточное условие экстремума).

Если 1) в точке функциядифференцируема и,2) существует вторая производная, 3) в окрестности, то прифункция имеет минимум, а при– максимум.

Итак, при исследовании функции на экстремум необходимо пользоваться правилами:

1. Найти первую производную

2. Найти критические точки , решив уравненияи.

3. Проверить, меняет ли знак первая производная при переходе через точку или установить знак второй производной, классифицировать экстремум.

4. Найти значение функции в экстремальных точках.

Задача. Исследовать на экстремум функцию .

Решение. Область определения ,

, при. Это значениене принадлежит области определения функции. Значит,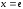– единственная критическая точка. Проверим знак первой производной слева и справа от нее.

При ,, функция возрастает, при,функция убывает, значит– точка максимума,– максимальное значение функции.

Наибольшее и наименьшее значение функции.

Теорема Вейерштрасса. Если функция непрерывна на замкнутом промежутке , то она достигает на нем наибольшее и наименьшее значения. Эти значения находятся либо на концах промежутка, либо в экстремальных точках.