matmod

Л.2. Типы математических моделей

Пример 1 (продолжение).

Математическая (структурная) модель рассматриваемой задачи:

Л.2. Типы математических моделей

Пример 1 (продолжение).

Из сохранения энергии колебательной системы:

Л.2. Типы математических моделей

Дискретные и непрерывные модели

Модели – как содержательные, так и математические – могут быть

дискретными,

непрерывными,

смешанными.

Между этими типами нет принципиального барьера и при уточнении или видоизменении модели дискретная картина может стать непрерывной и обратно; то же может произойти в процессе решения математической задачи

При составлении математической модели, а также при выборе метода ее исследования надо учитывать возможность применения как “дискретного”, так и “непрерывного” аппаратов

Л.2. Типы математических моделей

Пример 2. Изучается прогиб балки от груза, расположенного на интервале сравнительно малой длины.

Замена распределенного груза сосредоточенным

Пусть q(x) – плотность распределения груза на малом интервале (l), расположенном вблизи x = a.

R

Q = (l) q(x)dx – груз, сосредоточенный в точке.

q(x) ↔ q˜(x) = Qδ(x − a)

Подход дает возможность в случае сосредоточенной нагрузки пользоваться формулами, выведенными для нагрузки распределенной;

целесообразен, если конкретный вид функции q(x) нам неизвестен, но суммарное значение Q мы знаем.

Переход к дискретной модели нагрузки можно совершить, если имеется несколько грузов, каждый из которых распределен на малом интервале.

Л.2. Типы математических моделей

Пример 2 (продолжение).

Пусть грузов, замененных на сосредоточенные, много. Тогда может оказаться удобнее перейти к непрерывной модели нагрузки.

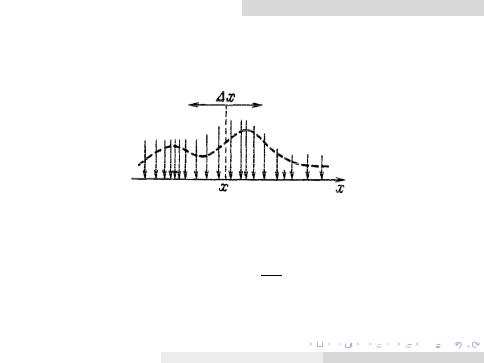
Эта плотность получается с помощью осреднения исходного распределения:

q(x) = q(x; x) = 1x Q(x; x).

Эпюра плотности нагрузки зависит от выбора интервала осреднения x. Он должен быть велик по сравнению с характерным расстоянием между грузами, но мал по сравнению с общей длиной балки.

2014 25 / 74

Л.2. Типы математических моделей

Аналогичная процедура осреднения происходит при переходе

от среды, состоящей из отдельных частиц к сплошной среде, параметры которой (плотность, температура и т. п.) распределены по пространству;

от поезда с дискретными вагонами к его непрерывной модели;

от воздействия на систему, имеющего характер частых подталкиваний, к непрерывно действующей силе и т. д.

Осреднение применяется не только для перехода от дискретной модели к непрерывной, но также и для упрощения быстро колеблющихся зависимостей в непрерывных моделях.

Л.2. Типы математических моделей

Внесение возможных неадекватностей при переходе дискретная ↔ непрерывная модель (Пример 3).

Пример 3. Продольные свободные упругие колебания прямолинейного однородного стержня.

u = u(x, t) – смещение в момент t сечения с координатой , отсчитываемой вдоль стержня.

Заменим непрерывную модель на дискретную: последовательность с шагом h материальных точек массы m = ρSh, соединенных пружинами нулевой массы и жесткости k = SE /h.

Л.2. Типы математических моделей

Пример 3 (продолжение).

ui (t) – смещение i-й точки.

Из второго закона Ньютона получаем систему ОДУ:

Замечание: ∂2u/∂x2 (непр. мод.) → симметричная разделенная разность второго порядка.

Л.2. Типы математических моделей

Пример 3 (продолжение).

Обратный переход от дискретной модели к непрерывной:

ui+1 = u(xi , t),

Решение системы ОДУ (дискретная модель) при малом h хорошо имитирует решение уравнения частных производных.

Проверка выполнения в модели математических аналогов фундаментальных физических законов (например, закон сохранения энергии) является важным этапом контроля качественной адекватности модели.

2014 29 / 74

Л.2. Типы математических моделей

Пример 3 (продолжение).

Проверка закона сохранения энергии E для стержня конечной длины ℓ, жестко закрепленного на концах (u|x=0,ℓ = 0, ut′ |x=0,ℓ = 0).

Непрерывная модель.