Введение.

Многозначные отображения естественно возникают в различных разделах математики: в теории игр, математической экономике, оптимальном управлении и т.д. Многозначные отображения естественно возникают также и в некоторых классических задачах функционального анализа, например, а задачах теории приближения и в теории аппроксимации.

Настоящая дипломная работа посвящена изучению некоторых свойств отображения метрической проекции на замкнутые выпуклые множества.

Дипломная работа состоит из 4 параграфов.

В §1 изучаются свойства метрической проекции в гильбертовом пространстве. Доказывается, что метрическая проекция в этом случае является однозначным отображением, липишцевым с константой 1. Изучены также другие свойства этого отображения.

В §2 дается определение и изучаются свойства метрики Хауедорфа в пространстве замкнутых подмножеств. В нем даются также основные определения и свойства полунепрерывных сверху многозначных отображений.

§3 дипломной работы посвящен изучению метрической проекции в банаховом пространстве. Он состоит из двух пунктов. В пункте 3.1 изучается метрическая проекция на компактное выпуклое подмножество в банаховом пространстве, показывается, что метрическая проекция является многозначным полунепрерывным сверху отображением. Посчитан пример. В пункте 3.2 изучаются свойства метрической проекции на замкнутое ограниченное множество в банаховом пространстве.

В §4 рассматриваются некоторые приложения метрической проекции в различных задачах. В пункте 4.1 метрическая проекция применяется для доказательства существования непрерывного сечения непрерывного многозначного отображения с выпуклыми замкнутыми образами. В пункте 4.2 метрическая проекция применяется для доказательства одной теоремы о неподвижной точке для многозначных отображений.

Содержание.

Введение блаблабла потом не забыть написать

§1. Метрическая проекция в гильбертовом пространстве.

Пусть Е – линейное пространство.

1.1. Определение.Говорят, что в линейном пространстве Е определено скалярное произведение, если каждой паре векторовx,yпоставлено в соответствие действительное число, обозначаемое (x,y), причем это соответствие обладает следующими свойствами:

1) для любого вектора 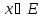число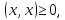причем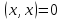тогжда и только тогда, когда;

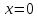2) 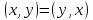для любых;

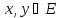3) 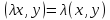, где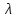– действительно число;

4) 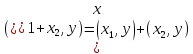– дистрибутивность.

1.2. Определение. Линейное пространство Е называется нормированным, если в нем каждому вектору х поставлено в соответствие число, называемое нормой х и обозначаемое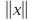причем это соответствие обладает свойствами:

1) 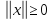, причем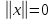тогда и только тогда, когда;

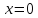2) 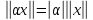для любых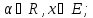

3) 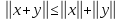для любых.

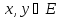Пусть Е – пространство со скалярным произведением, тогда положим

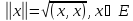
Очевидно, что 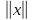удовлетворяет всем свойствам нормы.

Последовательность 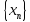точек пространства Е будем называть фундаментальной, если она удовлетворяет критерию Коши, т.е. если для любого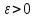существует такое число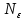?Xnj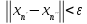для всех,.

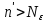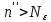1.3. Определение. Если в пространстве Е любая фундаментальная последовательность сходится, то это пространство называется полным.

1.4. Определение.Гильбертовым пространством Н называется пространство, полное относительно нормы, порожденной введенным в этом пространстве скалярным произведением.

1.5. Определение.Полное нормированное пространство называется Банаховым пространством.

1.6. Лемма. Каковы бы ни были элементы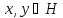, для них справедливо равенство параллелограмма

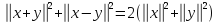
Доказательство.По определению нормы имеем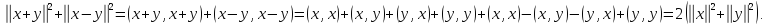

1.7. Определение.Пусть К – непустое замкнутое множество в пространстве Н. Для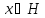положим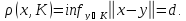Очевидно, что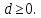Неотрицательное числоdназывается расстоянием от точки х до множества К.

1.8. Теорема.Пусть Р – гильбертово пространство, Л – непустое выпуклое замкнутое множество в Р. Тогда для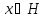существует и единственная точка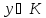такая, что выполняется равенство(1.1)

Доказательство.Пусть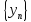– минимализирующая последовательность, т.е.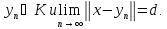В силу выпуклости множества К точк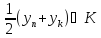а, откуда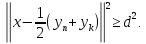Положим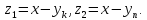Используя правило параллелограмма, распишем следующее выражение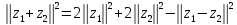.Подставляя вместо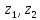указанные выше обозначения, получим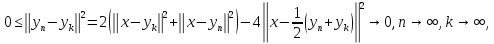так как вычитаемое имеет нижний предел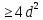, а уменьшаемое стремиться к. Следовательно, последовательность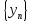является фундаментальной. Поскольку К – замкнутое множество, а пространство Н полно, то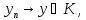при этом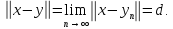Покажем, что точка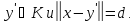Тогда в силу выпуклости множества К,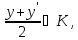так чт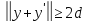о. Однако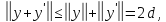и потому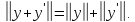Это равенство, как легко видеть, возможно только в том случае, когда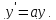Следовательно,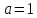и. Теорема доказана.

Пусть К – выпуклое замкнутое множество пространства Н. Согласно доказанной теореме каждому 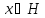однозначно соответствует точка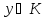такая, что выполняется равенство (1.1). Тем самым в Н определен оператор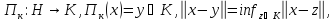который называется метрической проекцией пространства Н на множество К.

Изучим свойства метрической проекции.

1.9. Лемма. Равенство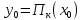выполняется тогда и только тогда, когда для любой точки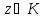выполняется неравенство

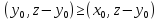(1.2)

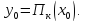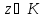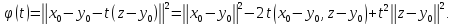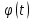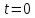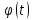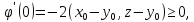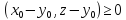Доказательство. Необходимость. Предположим, чтоВозьмем произвольную точку. В силу выпуклости множества К точкаРассмотрим функциюФункцияимеет минимум на отрезке [0,1] в точке 0, так как расстояние является кратчайшим при. Вычислим производнуюв точке 0:тогдадля любого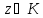. Из последнего неравенства вытекает, что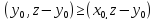для любого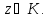

Достаточность.Предположим, что для любой точки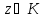выполнено (1.1). Свернем это неравенство, тогда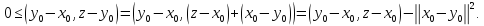Откуда, воспользовавшись неравенством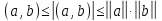, получим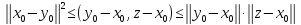. Возможны два случая: 1)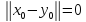, тогда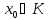и кратчайшее расстояние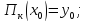2)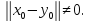Получим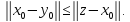Следовательно,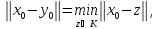откуда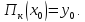Утверждение доказано.

1.10. Теорема.Пусть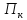– метрическая проекция гильбертова пространства Н на выпуклое замкнутое множество. Тогда для любых точек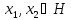выполняется неравенство

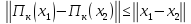(1.3)

Доказательство.Обозначим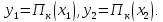В силу доказанной леммы для любой точки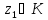справедливо неравенство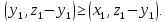Положив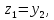получим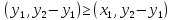(1.4)

Для любой точки 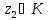справедливо неравенство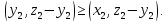Положив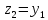, получим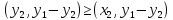(1.5)

Сложим неравенства (1.5) и (1.4)

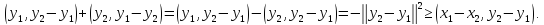Откуда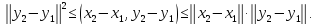Возможны два случая:

1) если 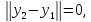то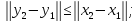

2) если 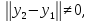то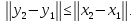Теорема доказана.

1.11. Следствие.Метрическая проекция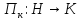является непрерывным отображением.

Доказательство.Отображение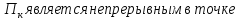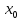, если для любого числа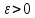найдется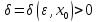такое, что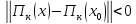как только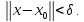Положив в неравенстве (1.2)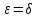получим требуемое утверждение.