- •Алгебра и аналитическая геометрия
- •4. Содержание дисциплины
- •§1. Основные понятия о множествах.
- •1.2 Способы задания множеств.
- •1.3 Отношения между множествами.
- •Определение 1.1
- •Определение 1.2
- •Определение 1.3
- •§2. Операции над множествами.
- •2.1 Пересечение множеств.
- •Определение 1.4
- •2.2 Объединение множеств.
- •2.3 Разность множеств. Определение 1.6
- •2.4 Дополнение к множеству. Определение 1.7
- •Определение 1.8
- •Тема 2. Матрицы
- •Тема 3. Система линейных уравнений.
- •Тема 4. Линейное пространство
- •Тема 5. Пространство геометрических векторов, как пример линейного пространства
- •§15.Уравнение прямой линии на плоскости.
- •10. Векторное, параметрическое, общее и каноническое уравнение прямой.
- •20. Взаимное расположение прямых на плоскости. Полуплоскости.
- •30. Прямая линия на плоскости с прямоугольной системой координат. Нормальное уравнение прямой.
- •§ 16. Уравнение плоскости в пространстве.
- •§ 17. Уравнение прямой в пространстве.
2.4 Дополнение к множеству. Определение 1.7
![]()
![]()
![]() Пусть В А.
Множество всех элементов множества А,
не принадлежащих множеству В, называют
дополнением к множеству В и
обозначают
Пусть В А.
Множество всех элементов множества А,
не принадлежащих множеству В, называют
дополнением к множеству В и
обозначают ![]() или
или ![]() .
.
Если
ясно, о каком множестве идёт речь, то
индекс А опускается
и пишут ![]() или
или ![]() .
.
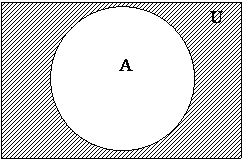
Определение 1.8
Пусть А –
некоторое множество, являющееся частью
универсального (основного) множества U.
Дополнением множества А называется
множество, состоящее из всех тех
и только тех элементов их множества U,
которые не принадлежат А. Его
обозначают ![]() или
или ![]() .
.
Это определение может быть записано в виде:
![]() =
{x xA}. (10)
=
{x xA}. (10)
Графически дополнения (соответственно определениям 1.7 и 1.8) изображены на рис. 19 и 20 соответственно, на которых дополнения заштрихованы.
|
|
|
|
|
|
|
|
|
|
рис. 19 рис. 20
Тема 2. Матрицы
1о .Основные определения.
Пусть
![]() – коммутативное кольцо с единицей.
– коммутативное кольцо с единицей.
Определение 1.
Матрицей
размеров
![]() над кольцом
над кольцом
![]() называется прямоугольная таблица из
называется прямоугольная таблица из![]() элементов кольца
элементов кольца![]() и имеющая
и имеющая![]() строк и
строк и![]() столбцов:
столбцов:

где
![]() –
номер строки,
–
номер строки,![]() – номер столбца,
– номер столбца,![]() − элементы матрицы,
− элементы матрицы,![]() и
и![]() − порядки матрицы. В этом случае говорят,
рассматриваемая матрица размера
− порядки матрицы. В этом случае говорят,
рассматриваемая матрица размера
![]() .
Если
.
Если
![]() ,
то матрица называетсяквадратной,
а число
,
то матрица называетсяквадратной,
а число
![]() – её порядком.
– её порядком.
Далее для изображения матрицы применяются либо круглые скобки, либо сдвоенные прямые:
 или
или
 .
.
Для краткого
обозначения матрицы используется либо
заглавная латинская буква
![]() ,
либо символы
,
либо символы![]() ,
,![]() ,
либо с разъяснением:
,
либо с разъяснением:![]() .
.
Множество всех
матриц размера
![]() обозначается
обозначается![]() .
.
Частные случаи матриц.
Если
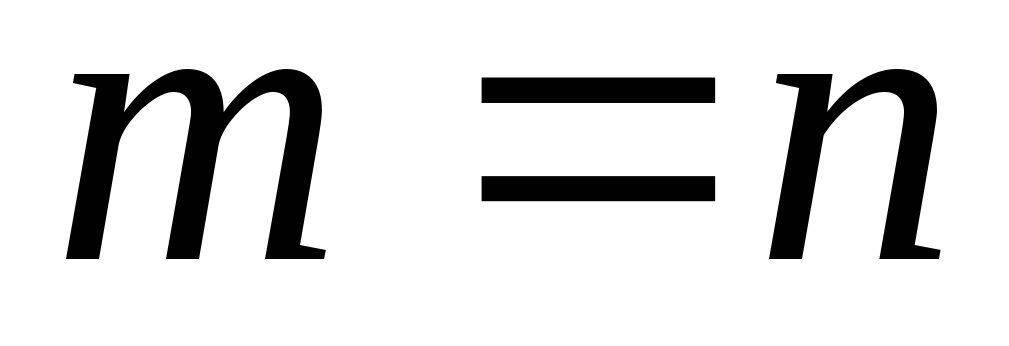 ,
то матрица называетсяквадратной.
Её диагональ
,
то матрица называетсяквадратной.
Её диагональ
 называетсяглавной
диагональю,
а
называетсяглавной
диагональю,
а
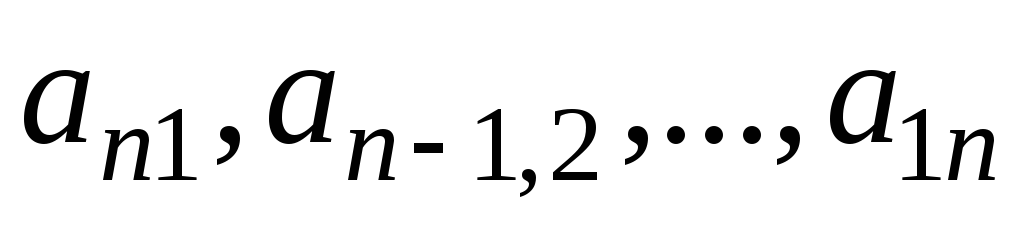 –побочной
диагональю.
–побочной
диагональю.Диагональная матрица – это матрица, у которой все ненулевые элементы находятся на главной диагонали, т.е.
 .
.Диагональная матрица вида
 называетсяскалярной.
называетсяскалярной.Скалярная матрица с единичными элементами на главной диагонали называется единичной. Обозначается
 или
или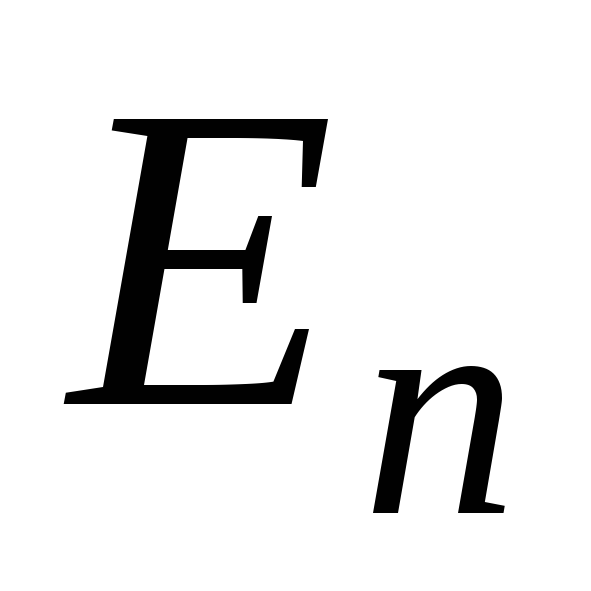 ,
где
,
где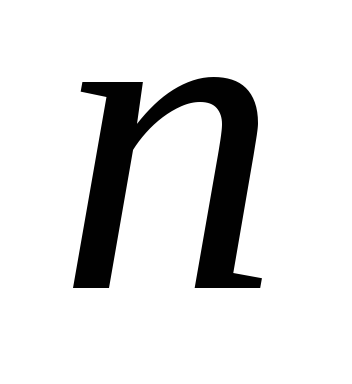 – ее порядок.
– ее порядок.Матрица размера
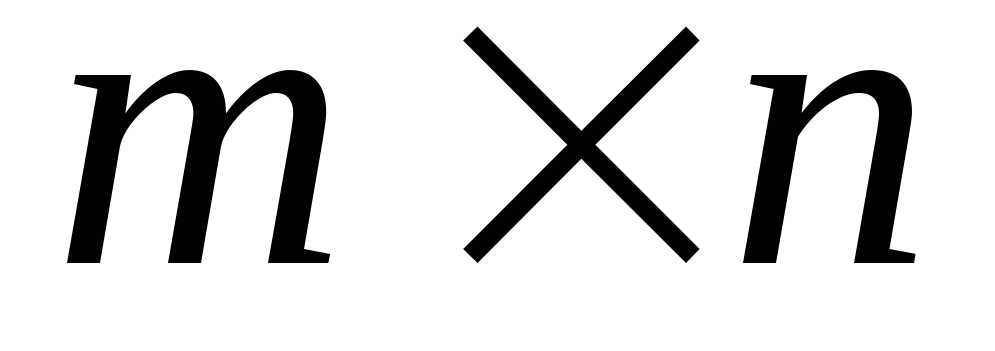 ,
у которой все элементы равны нулю,
называется нулевой
и обозначается
,
у которой все элементы равны нулю,
называется нулевой
и обозначается
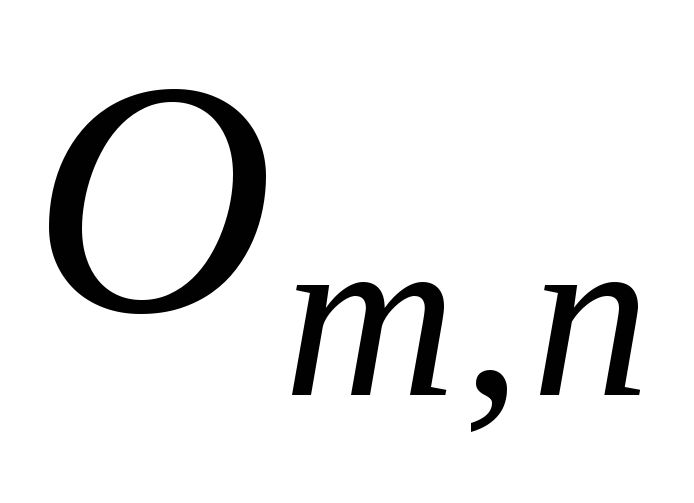 .
.Если
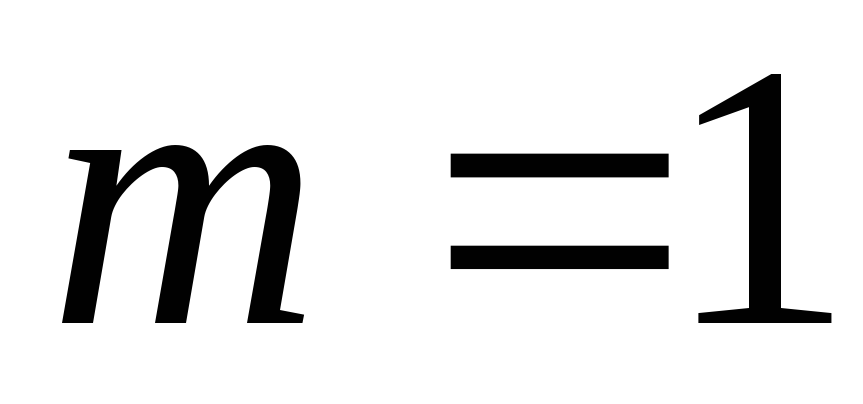 ,
то матрица называетсястрокой,
или матрица-строка,
или строка.
Если
,
то матрица называетсястрокой,
или матрица-строка,
или строка.
Если
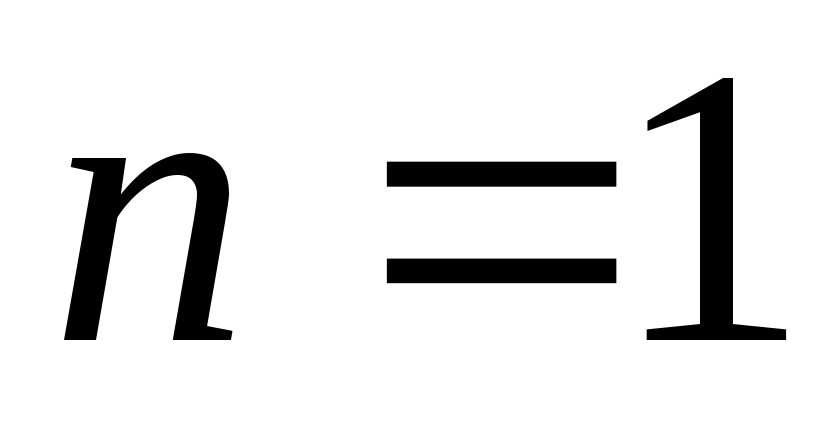
 столбцовая
= матрица-столбец
= столбец.
столбцовая
= матрица-столбец
= столбец.
Определение 2. Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.
2о. Операции над матрицами и их свойства.
Определение 3.
Суммой
матриц
![]() и
и![]() (т.е. имеющих одинаковые порядки)
называется матрица
(т.е. имеющих одинаковые порядки)
называется матрица![]() :
:![]() .
.
Обозначение:
![]() .
.
Замечание. Сумма матриц – алгебраическая операция.
Пример.
![]() .
.
Свойства (сложения матриц).
1) Коммутативность
сложения, т.е.,
![]() справедливо
справедливо![]() .
.
2) Ассоциативность
сложения, т.е.,
![]() справедливо
справедливо![]() .
.
3)
![]() .
.
4)
![]() .
При этом, если
.
При этом, если![]() ,
то
,
то![]() .
Матрица
.
Матрица![]() называетсяпротивоположной
к
называетсяпротивоположной
к
![]() и обозначается
и обозначается![]() .
.
Доказательство свойств – самостоятельно прямыми вычислениями.
Теорема 1.
Множество
![]() относительно сложения образует абелеву
группу.
относительно сложения образует абелеву
группу.
Доказательство следует из свойств 1)–4).
Определение 4.
Произведением
элемента
![]() на матрицу
на матрицу![]() называется матрица
называется матрица![]()
Обозначение:
![]() .
.
Операция,
сопоставляющая
![]() и
и![]() их произведение
их произведение![]() называетсяумножением
элемента кольца на матрицу.
называетсяумножением
элемента кольца на матрицу.
Свойства (умножения матрицы на элемент кольца).
![]() выполняется
выполняется
1)
![]() .
.
2)
![]() .
.
3)
![]() .
.
4)
![]() .
.
Доказательство свойств – самостоятельно прямыми вычислениями.
Замечание.
Разность
![]() двух прямоугольных матриц
двух прямоугольных матриц![]() и
и![]() определяется равенством
определяется равенством![]() .
.
Определение 5.
Произведением
матриц
![]() размера
размера![]() и
и![]() размера
размера![]() называется матрица
называется матрица![]() размеров
размеров![]() такая, что каждый элемент
такая, что каждый элемент![]() .
.
Обозначение:
![]() .
.
Операция произведения
![]() на
на![]() называетсяперемножением
этих матриц.
называетсяперемножением
этих матриц.
Из определения
следует, что элемент матрицы
![]() ,
стоящий в
,
стоящий в![]() –ой
строке и
–ой
строке и![]() –ом
столбце, равен сумме произведений
элементов
–ом
столбце, равен сумме произведений
элементов![]() –ой
строки матрицы
–ой
строки матрицы![]() на
на![]() –ый
столбец матрицы
–ый
столбец матрицы![]() .
.
Примеры.
1)
![]() ,
,
2)
![]() .
.
Таким образом, две
матрицы можно перемножать, если число
столбцов матрицы
![]() равно числу строк матрицы
равно числу строк матрицы![]() .
Тогда матрица
.
Тогда матрица![]() называетсясогласованной
с
называетсясогласованной
с
![]() .
Из согласованности
.
Из согласованности![]() с
с![]() не следует согласованность
не следует согласованность![]() с
с![]() .
Если даже условие согласования
выполняется, то в общем случае
.
Если даже условие согласования
выполняется, то в общем случае![]() .
.
Свойства (умножения матриц).
1) Ассоциативность
умножения матриц, т.е.,
![]() справедливо
справедливо![]() .
.
Доказательство.
Из определения 5 следует, что элемент
![]() матрицы
матрицы![]() равен
равен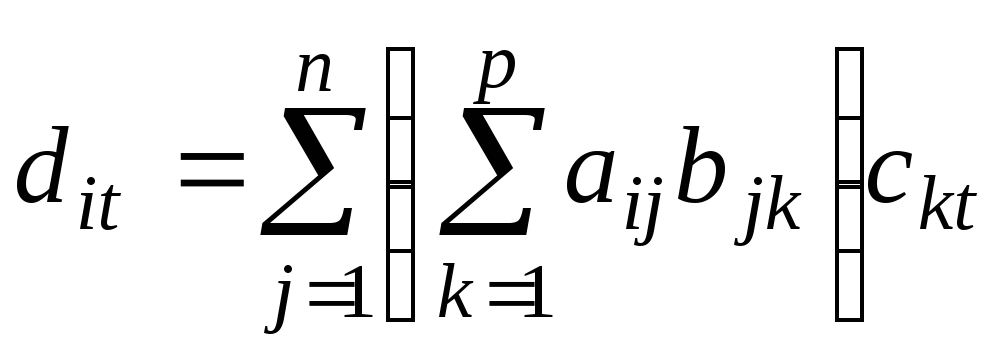 ,
а элемент
,
а элемент![]() матрицы
матрицы![]() равен
равен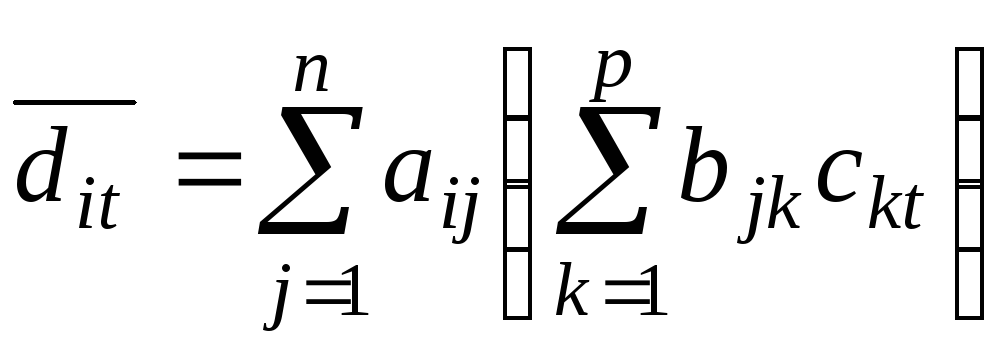 .
Равенство
.
Равенство![]() следует из возможности изменения порядка
суммирования.
следует из возможности изменения порядка
суммирования.
2) Дистрибутивность сложения относительно умножения, т.е.,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
Доказательство следует из определения суммы и произведения матриц.
3)
![]() .
.
Доказательство.
Пусть![]() ,
и
,
и![]() .
Тогда
.
Тогда![]() .
Здесь
.
Здесь![]() – символ Кронекера.
– символ Кронекера.
![]() .
.
4)
![]() .
.
5)
![]() .
.
Доказательство свойств 4)-5) проводится аналогично свойству 3).
6)
![]() .
.
Теорема 2.
Множество
![]() квадратных матриц порядка
квадратных матриц порядка![]() над
кольцом
над
кольцом![]() относительно операций сложения матриц
и умножения матриц образует кольцо с
единицей.
относительно операций сложения матриц
и умножения матриц образует кольцо с
единицей.
Доказательство.
Из теоремы 1
![]() – абелева группа. Так как любые матрицы
из
– абелева группа. Так как любые матрицы
из![]() согласованы
согласованы![]() умножение определено. Дистрибутивность
и ассоциативность умножения следует
из свойств 2) и 1). Свойство 3) демонстрирует
наличие единицы.■
умножение определено. Дистрибутивность
и ассоциативность умножения следует
из свойств 2) и 1). Свойство 3) демонстрирует
наличие единицы.■
Замечание. В общем случае произведение матриц не коммутативно. Например,
![]() .
.
Но из свойств 4) и
5)
![]() умножение квадратной матрицы на
умножение квадратной матрицы на![]() и
и![]() коммутирует. Также коммутирует умножение
квадратной матрицы на скалярную.
коммутирует. Также коммутирует умножение
квадратной матрицы на скалярную.
3о. Блочные матрицы.
Пусть матрица
![]() при помощи горизонтальных и вертикальных
прямых разбита на отдельные прямоугольные
клетки, каждая из которых является
матрицей меньших размеров и называетсяблоком
исходной матрицы.
В этом случае
при помощи горизонтальных и вертикальных
прямых разбита на отдельные прямоугольные
клетки, каждая из которых является
матрицей меньших размеров и называетсяблоком
исходной матрицы.
В этом случае
![]() рассматривается как некоторая новая,блочная
матрица
рассматривается как некоторая новая,блочная
матрица
![]() ,
элементами которой являются блоки
,
элементами которой являются блоки![]() указанной матрицы (
указанной матрицы (![]() – элементы матрицы, поэтому
– элементы матрицы, поэтому![]() заглавное). Здесь
заглавное). Здесь![]() – номер блочной строки,
– номер блочной строки,![]() – столбца.
– столбца.
Например, если
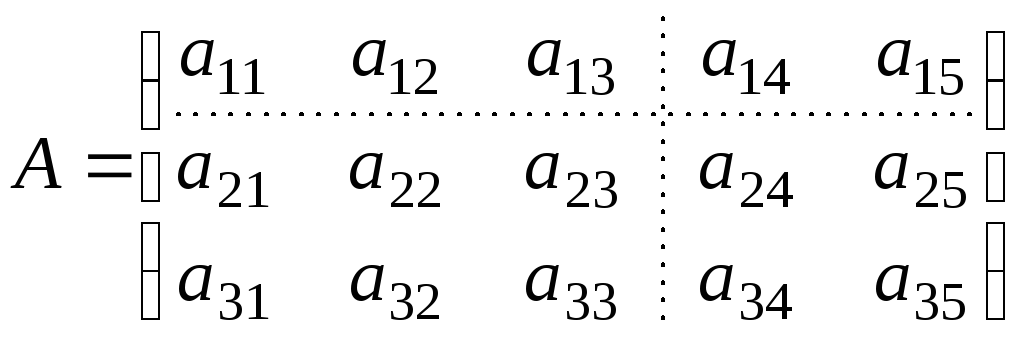 ,
то
,
то
![]() ,
,
![]() ,
,
 ,
,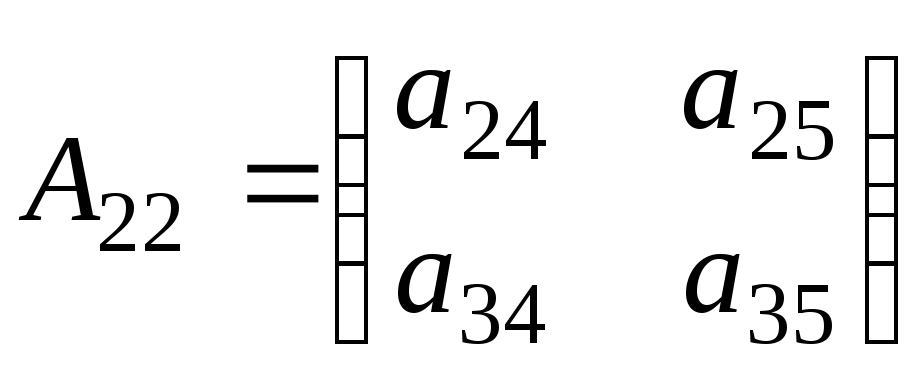 .
.
Замечательным
является факт, что операции с блочными
матрицами совершаются по тем же правилам,
что и обычными, только в роли элементов
выступают блоки. Действительно, если
![]() ,
то
,
то![]() ,
где
,
где![]() вычисляется по обычному правилу умножения
матрицы на число. Аналогично, если
вычисляется по обычному правилу умножения
матрицы на число. Аналогично, если![]() и
и![]() имеют одинаковые порядки и одинаковым
образом разбиты на блоки, то сумме
имеют одинаковые порядки и одинаковым
образом разбиты на блоки, то сумме![]() отвечает блочная матрица
отвечает блочная матрица![]() :
:![]() .
.
Для умножения
![]() на
на![]() необходимо согласовать их разбиение
на блоки, т.е. число столбцов каждого
блока
необходимо согласовать их разбиение
на блоки, т.е. число столбцов каждого
блока![]() равно числу строк блока
равно числу строк блока![]() .
Тогда
.
Тогда![]() .
.
Для доказательства
необходимо расписать правую и левую
части в терминах обычных элементов
матриц
![]() .
Пусть
.
Пусть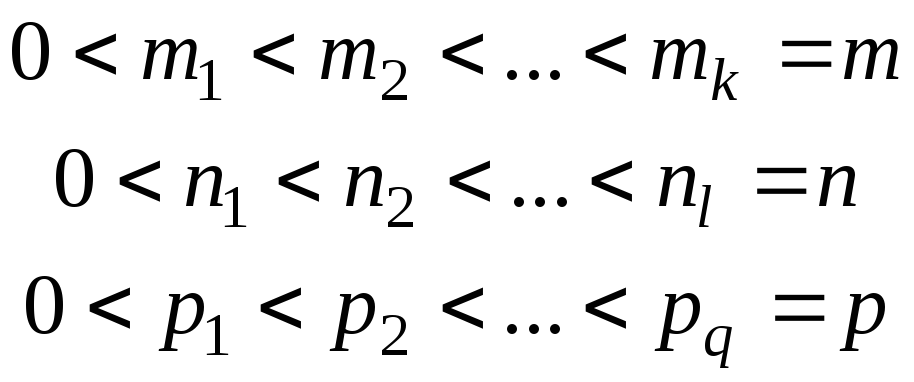 .
Если
.
Если![]() ,
то
,
то![]() и
и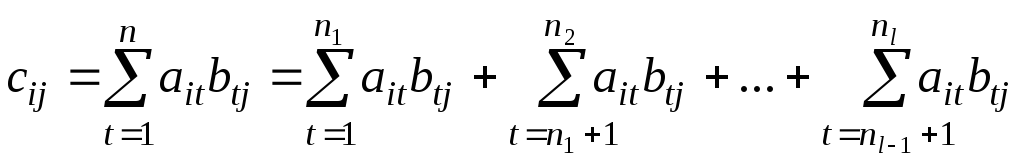 ,
откуда следует, что
,
откуда следует, что
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Пример.
Пусть
 ,
, ,
т.е.,
,
т.е.,
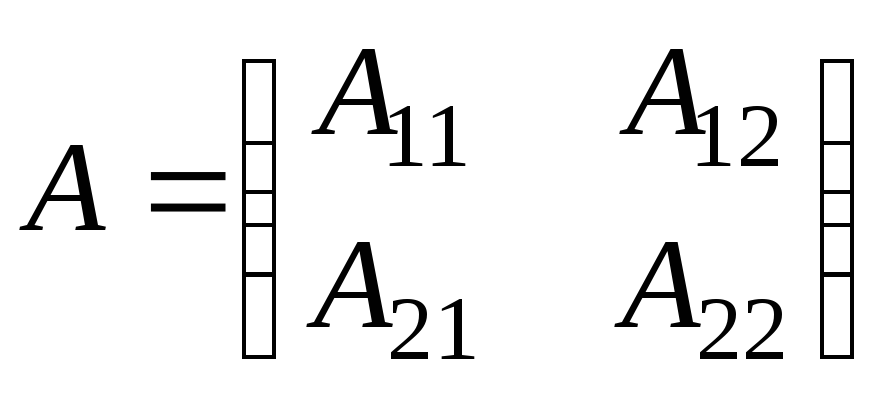 ,
,
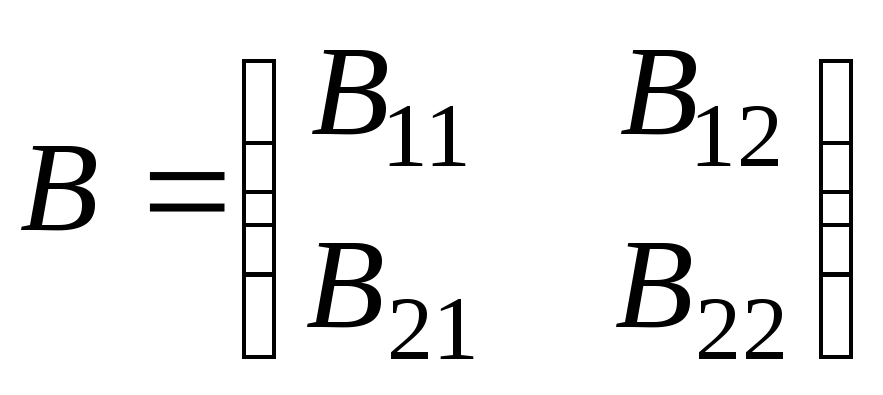 ,
,
где
![]() ,
,
![]() .
.
Тогда
![]() .
Аналогично находятся остальные
.
Аналогично находятся остальные![]() .
В результате получаем
.
В результате получаем
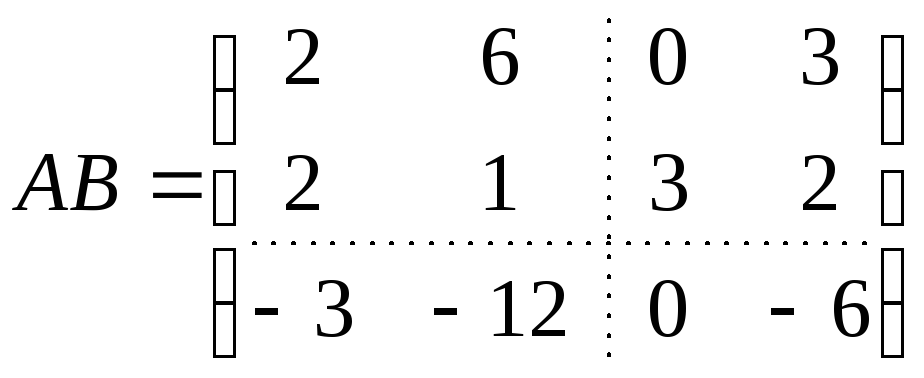 .
.
В качестве применения блочных матриц рассмотрим
Определение 6.
Прямой суммой
квадратных матриц
![]() порядков
порядков![]() соответственно называется квадратная
матрица
соответственно называется квадратная
матрица![]() порядка
порядка![]() :
:![]() .
.
Обозначение:
![]() .
.
Свойства (прямой суммы).
1)
![]() .
.
2)
![]() .
.
3)
![]() .
.
4)
![]() .
.